14.2.1平方差公式课件
文档属性
| 名称 | 14.2.1平方差公式课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 927.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-21 00:00:00 | ||
图片预览






文档简介
课件19张PPT。14.2.1 平方差公式 (a+b)(m+n)am+an+bm+bn回忆:多项式与多项式相乘的法则 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.=观察上述等式左边,你能发现什么规律?计算下列多项式,你能发现什么规律? (1) (x+1)(x-1)
(2) (1+2x) (1-2x)
(3) (-a -b) (-a + b)
(4) (a+b)(a-b)=x2-x+x-1=a2-ab+ab-b2=1-2x+2x-4x2=(-a) 2-ab+ab-b2-x+x-2x+2x-ab+ab运算出结果后,你又发现什么规律?等式的左边:两个数的和与这两个数的差的积, 等式的右边:是这两个数的平方差.= x2-1= 1-4x2= a 2- b2 = a2-b2 -ab+ab14.2.1 平方差公式(a + b) (a- b) a2- b2即两个数的和与这两个数的差的积,
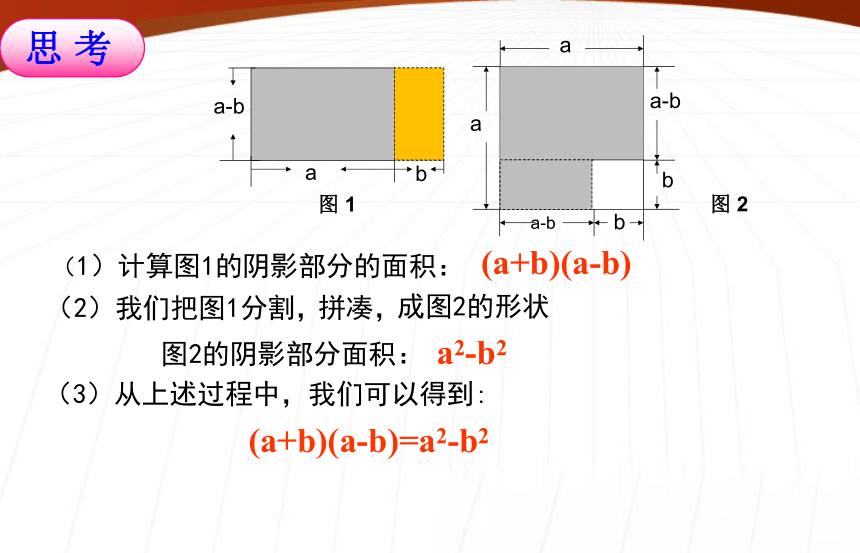
等于这两个数的平方差.=(3)从上述过程中,我们可以得到:(2)我们把图1分割,图 1图 2(a+b)(a-b)=a2-b2(a+b)(a-b)a2-b2图2的阴影部分面积:成图2的形状(1)计算图1的阴影部分的面积:拼凑,(a+b)(a-b)= a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。公式中的a和b,既可以是具体的数,也可以是单项式或者多项式;1、下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1-x);
(2)(-5+b)(5-b);
(3)(-m-n)(m-n);
(4)(c2-d2)(d2+c2) ;
(5)(a+1)(b-1) .(1)(a+b)(a-b)=a2-b2符号相同符号相反(4)(3)当堂训练2.根据公式直接计算:
(1) (x+y)(x-y)
(2) (a+5)(5-a)
(3) (-c-a) (-c+a)
(4) (x-3) (-3-x) (a+b)(a-b)=a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。????当堂训练(2)(2b+a)(a-2b)=4b2 -a2 ( ) (3)(-m–n )(-m +n)=m2 -n2 ( ) (1)(2+3x)(2?3x)=4?3x2 ( ) (4)(x+1)(y-1)= xy2-1 ( )xy –x+y-1×××√a2 -4b24- 9x2(a+b)(a-b)=a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。3.判断正误并更正:当堂训练(2) (?x + 2y)(?x ? 2y)
解: (1) (3x+2)(3x?2)=3x3x第一数a(3x)2 ?2 29x2 ? 4;=( - x )2?(2y )2=x2 ? 4y2 .(1) (3x+2 )( 3x-2 ) ;(2) (-x+2y)(-x-2y).例1 运用平方差公式计算:=1.利用平方差公式计算:(3) (3m-4n)(-4n-3m); (1) (a+3b)(a-3b); 大显身手(2) (3+2a)(-3+2a); ?=a2 ? 9b2 ??=4a2 ?9???2. 口算:大显身手?????=9999=9996=9991??3. 计算:大显身手??????1、先化简,再求值 ??????5x = -5x = -12、解方程:当a=1时,?1、本节课学习了哪些主要内容?(a+b)(a-b)=a2-b2.3、应用平方差公式时要注意什么?2、平方差公式的特点是什么?作 业:第112页:第1题???思维转换-x+y2m+ 3n5 - a2m-3n填空-2m+ 3n-2m-3n(4)(2013·郴州)已知a+b=4,a-b=3,则a2-b2=______ 计算解:原式=[(x+6)+(x-6)][(x+6)-(x-6)]????= (x+6+x-6)(x+6-x+6)?= 24x??谢谢指导
(2) (1+2x) (1-2x)
(3) (-a -b) (-a + b)
(4) (a+b)(a-b)=x2-x+x-1=a2-ab+ab-b2=1-2x+2x-4x2=(-a) 2-ab+ab-b2-x+x-2x+2x-ab+ab运算出结果后,你又发现什么规律?等式的左边:两个数的和与这两个数的差的积, 等式的右边:是这两个数的平方差.= x2-1= 1-4x2= a 2- b2 = a2-b2 -ab+ab14.2.1 平方差公式(a + b) (a- b) a2- b2即两个数的和与这两个数的差的积,
等于这两个数的平方差.=(3)从上述过程中,我们可以得到:(2)我们把图1分割,图 1图 2(a+b)(a-b)=a2-b2(a+b)(a-b)a2-b2图2的阴影部分面积:成图2的形状(1)计算图1的阴影部分的面积:拼凑,(a+b)(a-b)= a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。公式中的a和b,既可以是具体的数,也可以是单项式或者多项式;1、下列多项式乘法中,能用平方差公式计算的是( ):
(1)(x+1)(1-x);
(2)(-5+b)(5-b);
(3)(-m-n)(m-n);
(4)(c2-d2)(d2+c2) ;
(5)(a+1)(b-1) .(1)(a+b)(a-b)=a2-b2符号相同符号相反(4)(3)当堂训练2.根据公式直接计算:
(1) (x+y)(x-y)
(2) (a+5)(5-a)
(3) (-c-a) (-c+a)
(4) (x-3) (-3-x) (a+b)(a-b)=a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。????当堂训练(2)(2b+a)(a-2b)=4b2 -a2 ( ) (3)(-m–n )(-m +n)=m2 -n2 ( ) (1)(2+3x)(2?3x)=4?3x2 ( ) (4)(x+1)(y-1)= xy2-1 ( )xy –x+y-1×××√a2 -4b24- 9x2(a+b)(a-b)=a2-b2符号相同符号相反用符号相同的数(被减数)的平方减去符号相反的数(减数)的平方。3.判断正误并更正:当堂训练(2) (?x + 2y)(?x ? 2y)
解: (1) (3x+2)(3x?2)=3x3x第一数a(3x)2 ?2 29x2 ? 4;=( - x )2?(2y )2=x2 ? 4y2 .(1) (3x+2 )( 3x-2 ) ;(2) (-x+2y)(-x-2y).例1 运用平方差公式计算:=1.利用平方差公式计算:(3) (3m-4n)(-4n-3m); (1) (a+3b)(a-3b); 大显身手(2) (3+2a)(-3+2a); ?=a2 ? 9b2 ??=4a2 ?9???2. 口算:大显身手?????=9999=9996=9991??3. 计算:大显身手??????1、先化简,再求值 ??????5x = -5x = -12、解方程:当a=1时,?1、本节课学习了哪些主要内容?(a+b)(a-b)=a2-b2.3、应用平方差公式时要注意什么?2、平方差公式的特点是什么?作 业:第112页:第1题???思维转换-x+y2m+ 3n5 - a2m-3n填空-2m+ 3n-2m-3n(4)(2013·郴州)已知a+b=4,a-b=3,则a2-b2=______ 计算解:原式=[(x+6)+(x-6)][(x+6)-(x-6)]????= (x+6+x-6)(x+6-x+6)?= 24x??谢谢指导
