第23章 旋转单元复习 课件(共29张PPT)
文档属性
| 名称 | 第23章 旋转单元复习 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 11:31:53 | ||
图片预览




文档简介
(共29张PPT)
第23章 旋转单元复习
人教版九年级上册
教学目标
1.了解掌握旋转的概念、基本性质;
2. 掌握中心对称和中心对称图形的性质,能够识别中心对称图形;
3.了解关于原点对称的点的坐标之间的关系;
4.会运用旋转或中心对称的性质解决综合性问题.
知识模块
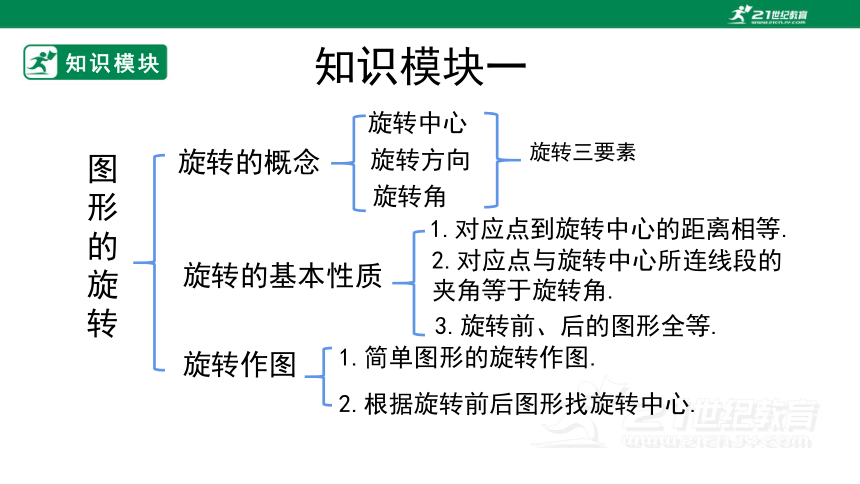
图形的旋转
旋转的基本性质
旋转角
旋转三要素
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
1.对应点到旋转中心的距离相等.
旋转作图
1.简单图形的旋转作图.
2.根据旋转前后图形找旋转中心.
旋转的概念
旋转中心
旋转方向
知识模块一
题型回顾
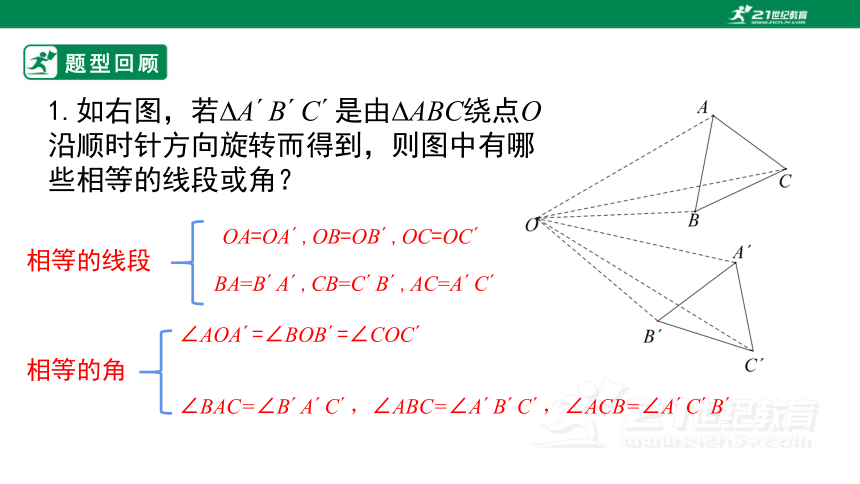
1.如右图,若 A B C 是由 ABC绕点O沿顺时针方向旋转而得到,则图中有哪些相等的线段或角?
相等的线段
∠AOA =∠BOB =∠COC
BA=B A ,CB=C B ,AC=A C
相等的角
OA=OA ,OB=OB ,OC=OC
∠BAC=∠B A C ,∠ABC=∠A B C ,∠ACB=∠A C B
题型回顾
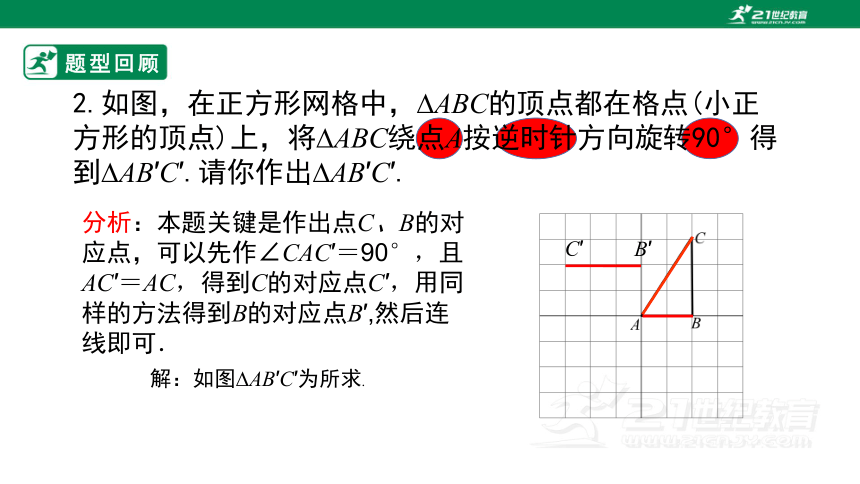
2.如图,在正方形网格中, ABC的顶点都在格点(小正方形的顶点)上,将 ABC绕点A按逆时针方向旋转90°得到 AB′C′.请你作出 AB′C′.
分析:本题关键是作出点C、B的对应点,可以先作∠CAC′=90°,且AC′=AC,得到C的对应点C′,用同样的方法得到B的对应点B′,然后连线即可.
C′
B′
解:如图 AB′C′为所求.
知识模块
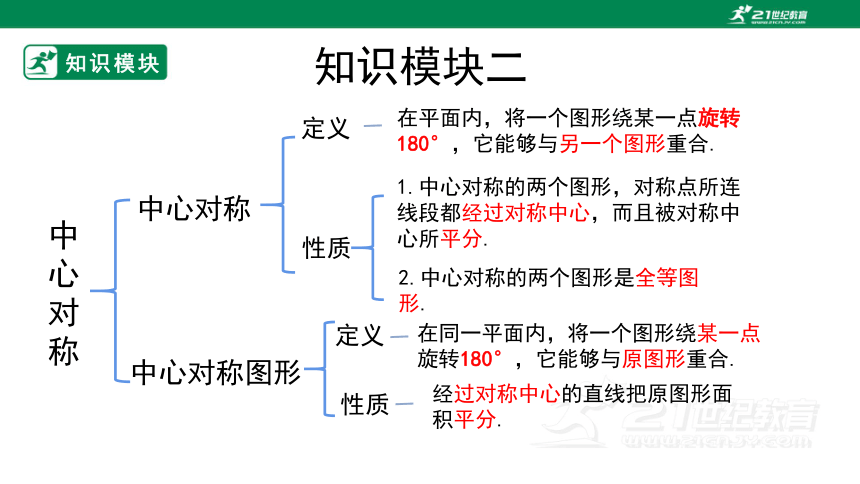
中心对称
中心对称
中心对称图形
定义
性质
经过对称中心的直线把原图形面积平分.
2.中心对称的两个图形是全等图形.
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
在平面内,将一个图形绕某一点旋转180°,它能够与另一个图形重合.
性质
知识模块二
定义
在同一平面内,将一个图形绕某一点
旋转180°,它能够与原图形重合.
题型回顾
经典题型回顾
1.在平面直角坐标系中,点P(x,y) 关于原点对称的点P' 的坐标是_________.
(-x,-y)
2.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为 .
3
题型回顾
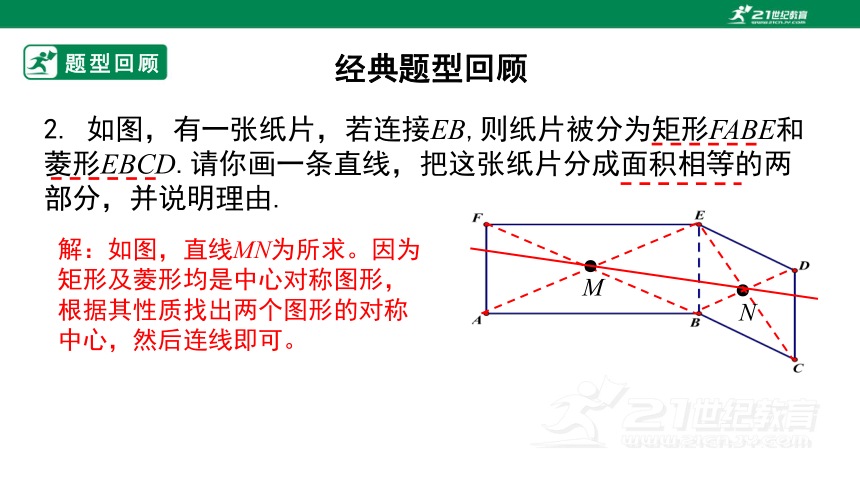
2. 如图,有一张纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD.请你画一条直线,把这张纸片分成面积相等的两部分,并说明理由.
●
●
M
N
解:如图,直线MN为所求。因为矩形及菱形均是中心对称图形,根据其性质找出两个图形的对称中心,然后连线即可。
经典题型回顾
典型例题
例1 如图,已知 ABD和 AEC都是等边三角形,则 AEB可以看作是 ACD绕点___沿逆时针方向旋转_______而得到.
A
60°
典型例题
拓展 若例1中,DC与BE相交于点F,则∠DFB=________ .
F
60 °
α
β
α
60 °
?
针对训练
针对性训练1 如图,将 ABC 绕点C 按顺时针方向旋转20 °,点 B 落在点 E 的位置,点 A 落在 D 点的位置,若AC⊥DE,则∠BAC 的度数为_______.
70 °
20 °
90 °
70 °
针对训练
针对性训练2 如图 ,6×6的正方形网格中, EFG绕某点旋转一定的角度,得到 HIJ,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
【解析】
可以作线段GJ与HE的垂直平分线,
交点便是旋转中心.
C
典型例题
例2 (1)下列图形中,既是轴对称图形,又是中心对称图形的是( ).
D
课堂小结
轴对称图形和中心对称图形的主要区别在于前者是沿某一条直线对折,后者是绕某一点旋转.这是易错点,也是辨别它们不同的关键.
识别方法总结
典型例题
(2)如图,平行四边形 ABCD的对称中心在坐标原点, AD∥BC ,顶点D(3,2) 、C(1,-2) ,则其他两个顶点的坐标为A , B .
(-1,2 )
(-3,-2 )
平行四边形是中心对称图形.
典型例题
例3 正方形ABCD的边长为 3,E、F分别是 AB、BC 边上的点,且∠EDF=45°,将△DAE 绕点D逆时针旋转90°得到△DCM.
(1)求证:EF=FM ;
(2)当AE=1时,求 EF 的长.
典型例题
分析:要证 EF=FM
DE=DM
∠ EDF= ∠ MDF
DF=DF
∠ DFE= ∠ DFM
∠ DEF= ∠ DMF
△DFE≌△DFM
DF=DF
公共边
DE=DM
旋转的性质
∠ EDF= ∠ MDF
45 °
S
S
A
典型例题
45 °
方法一
∠ EDF= ∠ MDF=45 °
∠ EDM=90°
∠ EDF= 45°
M
F
E
D
C
B
A
典型例题
45 °
∠ EDF= ∠ MDF=45 °
∠ ADE= ∠CDM=β
方法二
旋转的性质
α+β=45°
∠ MDF=α+β= 45°
M
F
E
D
C
B
A
∠ ADC=90°
∠ EDF= 45°
∠ EDF= 45°
β
β
α
方法一更简单!
典型例题
(1)证明:由旋转性质可知
DE=DM, ∠EDM=90 °,而∠EDF=45 °
∴ ∠ MDF=∠EDF=45 °
∵ 在△DFE与△DFM中
∴△DFE≌△DFM(SAS)
∴EF=FM
典型例题
(2)当AE=1时,求EF的长.
在Rt△EBF中, ∠ EBF=90 °
BE=3-1=2,BF=3-x
∴22+(3-x)2=(x+1)2
3-x
x
x+1
2
1
解:设FC=x,
则 FM=x+1=EF
1
解得 x=1.5
∴EF=1.5+1=2.5
课堂小结
解题方法总结
在证明线段相等或求线段长度问题时,若遇旋转有关背景,别忘记根据旋转性质找等边或等角!
课堂练习
1. 如图,△ABC 与△A'B'C' 关于点O成中心对称,则下列结论不成立的是( ).
A.点A与点A' 是对称点
B. BO=B'O
C. AB// A'B'
D. ∠ACB= ∠C'A' B'
分析:根据中心对称的定义及性质, A、B符合,D非对应角,故答案为D.
D
课堂练习
2.如图所示,四边形ABCD是正方形,ΔADE绕着点A旋转90°后到达ΔABF的位置,连接EF,则ΔAEF的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形
C
课堂练习
3.已知△ABC 中,A(-2,3),B(-1,2),C(-3,1).
请画出△ABC 关于原点 O 对称△A1B1C1.
如图△A1B1C1为所求.
参考方法:可以分别求出点A、B、C关于原点O对称的点A1、B1、C1的坐标,然后描点,连线即可.
A
B
C
A1
B1
C1
课堂总结
对照知识网络,看你掌握了多少?
旋转
图形的旋转
中心对称
旋转的概念
旋转的基本性质
旋转作图
中心对称
中心对称图形
提醒
把困惑记下来!
课堂总结
旋转是全等变换,遇到旋转问题时,要善于运用旋转前后图形全等性质解决问题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第23章 旋转单元复习
人教版九年级上册
教学目标
1.了解掌握旋转的概念、基本性质;
2. 掌握中心对称和中心对称图形的性质,能够识别中心对称图形;
3.了解关于原点对称的点的坐标之间的关系;
4.会运用旋转或中心对称的性质解决综合性问题.
知识模块
图形的旋转
旋转的基本性质
旋转角
旋转三要素
2.对应点与旋转中心所连线段的夹角等于旋转角.
3.旋转前、后的图形全等.
1.对应点到旋转中心的距离相等.
旋转作图
1.简单图形的旋转作图.
2.根据旋转前后图形找旋转中心.
旋转的概念
旋转中心
旋转方向
知识模块一
题型回顾
1.如右图,若 A B C 是由 ABC绕点O沿顺时针方向旋转而得到,则图中有哪些相等的线段或角?
相等的线段
∠AOA =∠BOB =∠COC
BA=B A ,CB=C B ,AC=A C
相等的角
OA=OA ,OB=OB ,OC=OC
∠BAC=∠B A C ,∠ABC=∠A B C ,∠ACB=∠A C B
题型回顾
2.如图,在正方形网格中, ABC的顶点都在格点(小正方形的顶点)上,将 ABC绕点A按逆时针方向旋转90°得到 AB′C′.请你作出 AB′C′.
分析:本题关键是作出点C、B的对应点,可以先作∠CAC′=90°,且AC′=AC,得到C的对应点C′,用同样的方法得到B的对应点B′,然后连线即可.
C′
B′
解:如图 AB′C′为所求.
知识模块
中心对称
中心对称
中心对称图形
定义
性质
经过对称中心的直线把原图形面积平分.
2.中心对称的两个图形是全等图形.
1.中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
在平面内,将一个图形绕某一点旋转180°,它能够与另一个图形重合.
性质
知识模块二
定义
在同一平面内,将一个图形绕某一点
旋转180°,它能够与原图形重合.
题型回顾
经典题型回顾
1.在平面直角坐标系中,点P(x,y) 关于原点对称的点P' 的坐标是_________.
(-x,-y)
2.已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为 .
3
题型回顾
2. 如图,有一张纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD.请你画一条直线,把这张纸片分成面积相等的两部分,并说明理由.
●
●
M
N
解:如图,直线MN为所求。因为矩形及菱形均是中心对称图形,根据其性质找出两个图形的对称中心,然后连线即可。
经典题型回顾
典型例题
例1 如图,已知 ABD和 AEC都是等边三角形,则 AEB可以看作是 ACD绕点___沿逆时针方向旋转_______而得到.
A
60°
典型例题
拓展 若例1中,DC与BE相交于点F,则∠DFB=________ .
F
60 °
α
β
α
60 °
?
针对训练
针对性训练1 如图,将 ABC 绕点C 按顺时针方向旋转20 °,点 B 落在点 E 的位置,点 A 落在 D 点的位置,若AC⊥DE,则∠BAC 的度数为_______.
70 °
20 °
90 °
70 °
针对训练
针对性训练2 如图 ,6×6的正方形网格中, EFG绕某点旋转一定的角度,得到 HIJ,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
【解析】
可以作线段GJ与HE的垂直平分线,
交点便是旋转中心.
C
典型例题
例2 (1)下列图形中,既是轴对称图形,又是中心对称图形的是( ).
D
课堂小结
轴对称图形和中心对称图形的主要区别在于前者是沿某一条直线对折,后者是绕某一点旋转.这是易错点,也是辨别它们不同的关键.
识别方法总结
典型例题
(2)如图,平行四边形 ABCD的对称中心在坐标原点, AD∥BC ,顶点D(3,2) 、C(1,-2) ,则其他两个顶点的坐标为A , B .
(-1,2 )
(-3,-2 )
平行四边形是中心对称图形.
典型例题
例3 正方形ABCD的边长为 3,E、F分别是 AB、BC 边上的点,且∠EDF=45°,将△DAE 绕点D逆时针旋转90°得到△DCM.
(1)求证:EF=FM ;
(2)当AE=1时,求 EF 的长.
典型例题
分析:要证 EF=FM
DE=DM
∠ EDF= ∠ MDF
DF=DF
∠ DFE= ∠ DFM
∠ DEF= ∠ DMF
△DFE≌△DFM
DF=DF
公共边
DE=DM
旋转的性质
∠ EDF= ∠ MDF
45 °
S
S
A
典型例题
45 °
方法一
∠ EDF= ∠ MDF=45 °
∠ EDM=90°
∠ EDF= 45°
M
F
E
D
C
B
A
典型例题
45 °
∠ EDF= ∠ MDF=45 °
∠ ADE= ∠CDM=β
方法二
旋转的性质
α+β=45°
∠ MDF=α+β= 45°
M
F
E
D
C
B
A
∠ ADC=90°
∠ EDF= 45°
∠ EDF= 45°
β
β
α
方法一更简单!
典型例题
(1)证明:由旋转性质可知
DE=DM, ∠EDM=90 °,而∠EDF=45 °
∴ ∠ MDF=∠EDF=45 °
∵ 在△DFE与△DFM中
∴△DFE≌△DFM(SAS)
∴EF=FM
典型例题
(2)当AE=1时,求EF的长.
在Rt△EBF中, ∠ EBF=90 °
BE=3-1=2,BF=3-x
∴22+(3-x)2=(x+1)2
3-x
x
x+1
2
1
解:设FC=x,
则 FM=x+1=EF
1
解得 x=1.5
∴EF=1.5+1=2.5
课堂小结
解题方法总结
在证明线段相等或求线段长度问题时,若遇旋转有关背景,别忘记根据旋转性质找等边或等角!
课堂练习
1. 如图,△ABC 与△A'B'C' 关于点O成中心对称,则下列结论不成立的是( ).
A.点A与点A' 是对称点
B. BO=B'O
C. AB// A'B'
D. ∠ACB= ∠C'A' B'
分析:根据中心对称的定义及性质, A、B符合,D非对应角,故答案为D.
D
课堂练习
2.如图所示,四边形ABCD是正方形,ΔADE绕着点A旋转90°后到达ΔABF的位置,连接EF,则ΔAEF的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形
C
课堂练习
3.已知△ABC 中,A(-2,3),B(-1,2),C(-3,1).
请画出△ABC 关于原点 O 对称△A1B1C1.
如图△A1B1C1为所求.
参考方法:可以分别求出点A、B、C关于原点O对称的点A1、B1、C1的坐标,然后描点,连线即可.
A
B
C
A1
B1
C1
课堂总结
对照知识网络,看你掌握了多少?
旋转
图形的旋转
中心对称
旋转的概念
旋转的基本性质
旋转作图
中心对称
中心对称图形
提醒
把困惑记下来!
课堂总结
旋转是全等变换,遇到旋转问题时,要善于运用旋转前后图形全等性质解决问题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
