3.3 代数式的值 复习题(含解析)苏科版七年级数学上册
文档属性
| 名称 | 3.3 代数式的值 复习题(含解析)苏科版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 86.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 22:39:06 | ||
图片预览



文档简介
3.3 代数式的值(复习题)-苏科版七年级上册
一.选择题
.已知a﹣2b2=3,则2022﹣2a+4b2的值是( )
A.2016 B.2028 C.2019 D.2025
.若x2﹣3x﹣2=0,则2x2﹣6x+2018的值为( )
A.2021 B.2022 C.2023 D.2024
.若x,y二者满足等式x2﹣2x=2y﹣y2,且xy=,则式子x2+2xy+y2﹣2(x+y)+2020的值为( )
A.2019 B.2020 C.2021 D.2022
.已知,当x=2时,ax3+bx+c的值是2022;当x=﹣2时,ax3+bx﹣c的值是( )
A.﹣2022 B.﹣2018 C.2018 D.2022
.如图是一个运算程序,能使输出结果m的值为6的是( )
A.x=1,y=2 B.x=﹣2,y=﹣2 C.x=2,y=1 D.x=3,y=﹣1
.当x=1时,代数式ax2﹣2bx+1的值为3,那么5﹣2a+4b的值是( )
A.1 B.2 C.3 D.4
.已知(x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,将x=0代入这个等式中可以求出a0=1.用这种方法可以求得a6+a5+a4+a3+a2+a1的值为( )
A.﹣16 B.16 C.﹣1 D.1
.下列关于代数式﹣m+1的值的结论:①﹣m+1的值可能是正数;②﹣m+1的值一定比﹣m大;③﹣m+1的值一定比1小;④﹣m+1的值随着m的增大而减小.其中所有正确结论的序号是( )
A.①②③ B.②③④ C.①②④ D.①③④
.已知关于x的多项式(m+3)x3﹣xn+x﹣mn为二次三项式,则当x=﹣1时,这个二次三项式的值是( )
A.7 B.6 C.4 D.3
.当x=1时,代数式px3+qx+1的值是﹣2020,则当x=﹣1时,代数式px3+qx+1的值是( )
A.2019 B.2020 C.2021 D.2022
二.填空题
.小王利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … ﹣2 4 ﹣8 16 ﹣32 …
那么,当输入数据是8时,输出的数据是 ;当输入数据是n时,输出的数据是 .
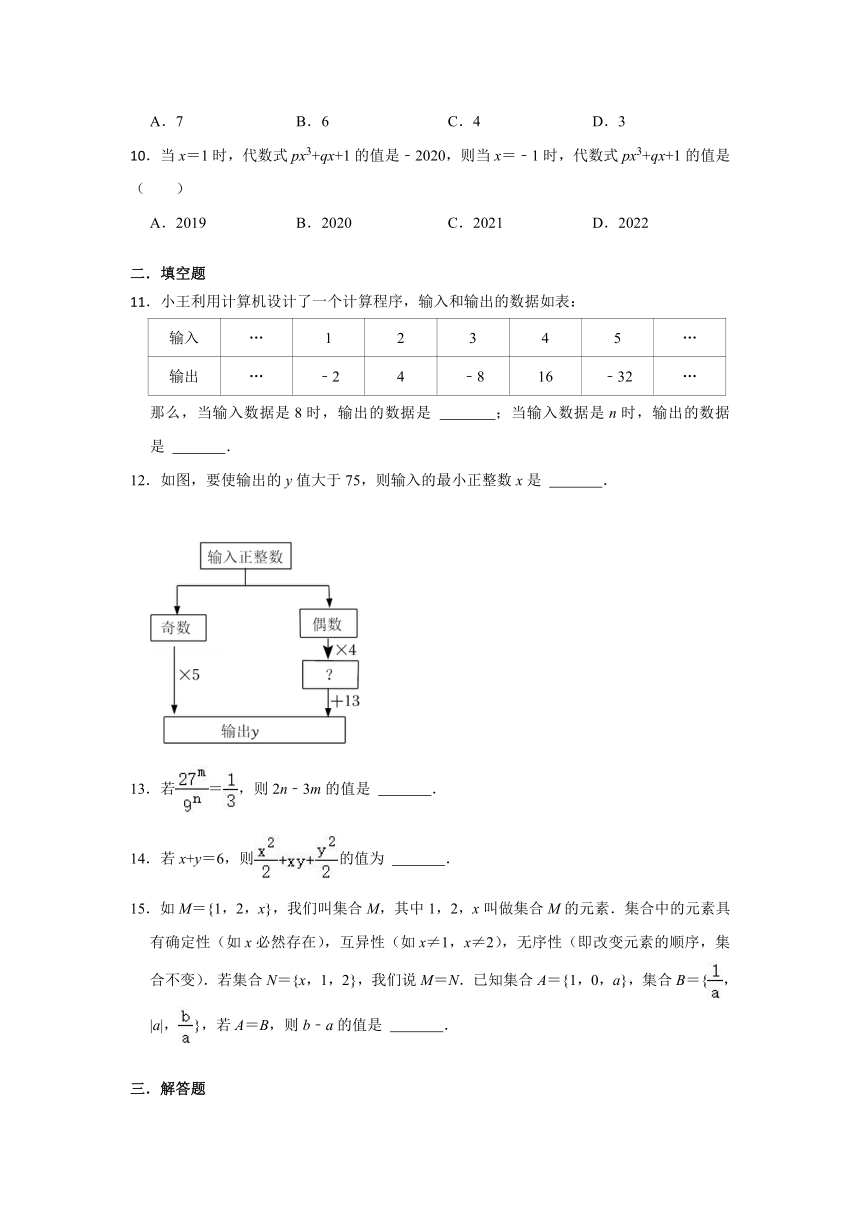
12.如图,要使输出的y值大于75,则输入的最小正整数x是 .
13.若=,则2n﹣3m的值是 .
14.若x+y=6,则的值为 .
15.如M={1,2,x},我们叫集合M,其中1,2,x叫做集合M的元素.集合中的元素具有确定性(如x必然存在),互异性(如x≠1,x≠2),无序性(即改变元素的顺序,集合不变).若集合N={x,1,2},我们说M=N.已知集合A={1,0,a},集合B={,|a|,},若A=B,则b﹣a的值是 .
三.解答题
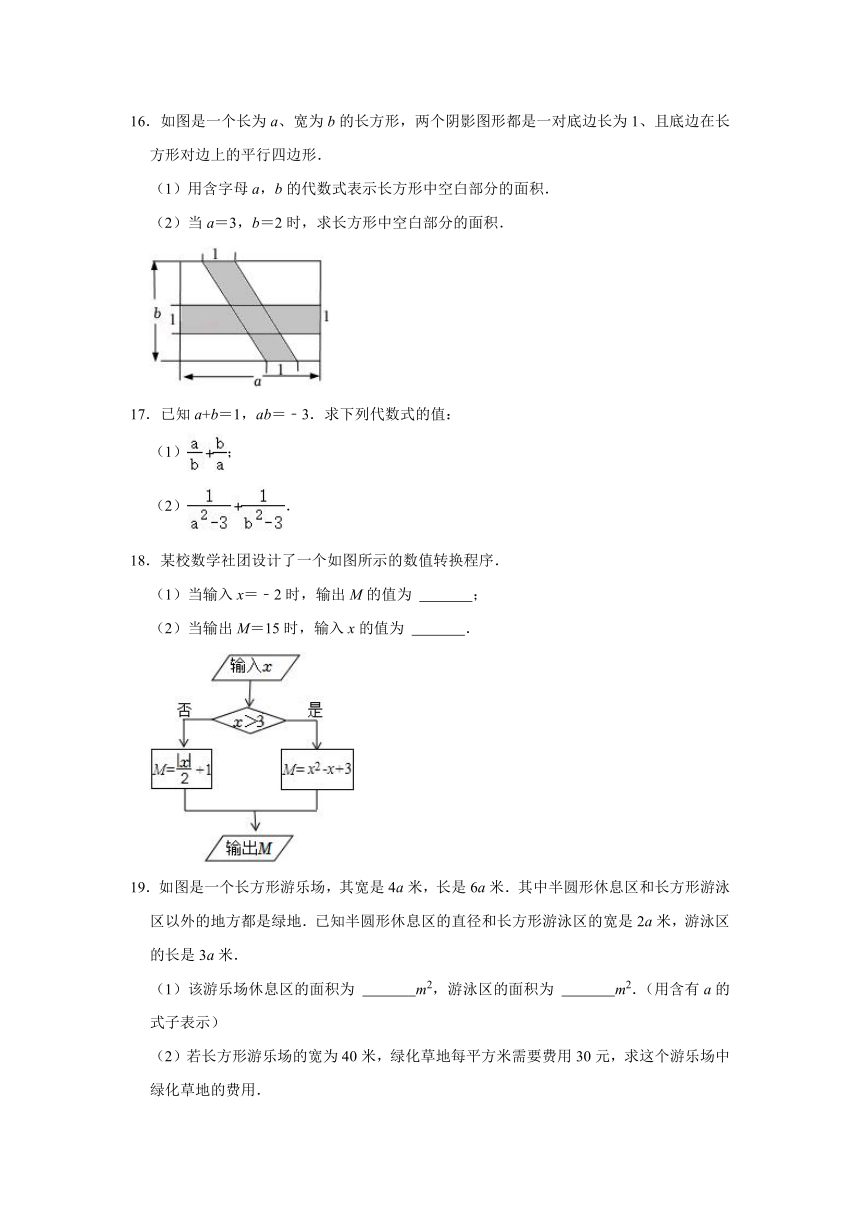
16.如图是一个长为a、宽为b的长方形,两个阴影图形都是一对底边长为1、且底边在长方形对边上的平行四边形.
(1)用含字母a,b的代数式表示长方形中空白部分的面积.
(2)当a=3,b=2时,求长方形中空白部分的面积.
17.已知a+b=1,ab=﹣3.求下列代数式的值:
(1);
(2).
18.某校数学社团设计了一个如图所示的数值转换程序.
(1)当输入x=﹣2时,输出M的值为 ;
(2)当输出M=15时,输入x的值为 .
19.如图是一个长方形游乐场,其宽是4a米,长是6a米.其中半圆形休息区和长方形游泳区以外的地方都是绿地.已知半圆形休息区的直径和长方形游泳区的宽是2a米,游泳区的长是3a米.
(1)该游乐场休息区的面积为 m2,游泳区的面积为 m2.(用含有a的式子表示)
(2)若长方形游乐场的宽为40米,绿化草地每平方米需要费用30元,求这个游乐场中绿化草地的费用.
20.某中学八年级(1)班5名老师决定带领本班x名学生去迁西景忠山旅游参观.该景区每张门票的票价为40元,现有A、B两种购票方案可供选择:方案A:教师全价,学生半价;方案B:不分教师与学生,全部六折优惠.
(1)请用含x的代数式分别表示选择A,B两种方案所需的费用;
(2)当学生人数x=50时,且只选择其中一种方案购票,请通过计算说明选择哪种方案更为优惠.
参考答案与试题解析
一.选择题
.【解答】解:2022﹣2a+4b2=2022﹣2(a﹣2b2),
∵a﹣2b2=3,
∴原式=2022﹣2×3=2016.
故选:A.
.【解答】解:∵x2﹣3x﹣2=0,
∴x2﹣3x=2,
∴2x2﹣6x+2018
=2(x2﹣3x)+2018
=2×2+2018
=4+2018
=2022,
故选:B.
.【解答】解:∵x2﹣2x=2y﹣y2,xy=
∴x2﹣2x+y2﹣2y=0,2xy=1.
∴x2+2xy+y2﹣2(x+y)+2020
=x2+2xy+y2﹣2x﹣2y+2020
=x2﹣2x+y2﹣2y+2xy+2020.
=0+1+2020
=2021.
故选:C.
.【解答】解:∵当x=2时,代数式ax3+bx+c的值为2022,
∴8a+2b=2022﹣c,
当x=﹣2时,
ax3﹣bx+3
=﹣8a﹣2b﹣c
=﹣(8a+2b)﹣c
=﹣2022+c﹣c
=﹣2022,
故选:A.
.【解答】解:∵选项A、C的y满足y≥0,把x、y的值代入m=x2﹣3y,
则选项A、C输出的值m分别为﹣5、1;
选项B、D的y满足y≤0,把x、y的值代入m=x2+3y,
则选项B、D输出的值m分别为10、6.
∴选项A、B、C都不满足输出m的值为6的条件,
选项D满足输出m的值为6的条件.
故选:D.
.【解答】解:根据题意,将x=1代入ax2﹣2bx+1=3,得:a﹣2b=2,
则5﹣2a+4b=﹣2(a﹣2b)+5=﹣2×2+5=﹣4+5=1.
故选:A.
.【解答】解:当x=1时,∵(x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,
∴a6+a5+a4+a3+a2+a1+a0=0.
∴a6+a5+a4+a3+a2+a1=﹣a0=﹣1.
故选:C.
.【解答】解:当m=0时,﹣m+1=1>0,故①符合题意;
∵﹣m+1﹣(﹣m)=1>0,
∴﹣m+1>﹣m,故②符合题意;
当m=0时,﹣m+1=1,故③不符合题意;
m越大,﹣m越小,﹣m+1越小,故④符合题意;
故选:C.
.【解答】解:∵关于x的多项式(m+3)x3﹣xn+x﹣mn为二次三项式,
∴m+3=0,n=2,
解得:m=﹣3,
∴关于x的多项式为﹣x2+x+6,
当x=﹣1时,
原式=﹣(﹣1)2+(﹣1)+6
=﹣1﹣1+6
=4,
故选:C.
.【解答】解:∵x=1时,代数式px3+qx+1的值是﹣2020,
∴把x=1代入px3+qx+1得,
p+q+1=﹣2020,
∴p+q=﹣2021,
∴﹣p﹣q=2021,
把x=﹣1代入px3+qx+1得,
﹣p﹣q+1
=2021+1
=2022,
故选:D.
二.填空题
【解答】解:设输入数据为a,输出数据为b,
当a=1时,b=﹣2=(﹣2)1,
当a=2时,b=4=(﹣2)2,
当a=3时,b=﹣8=(﹣2)3,
,
∴b=(﹣2)a,
∴当输入数据是8时,输出的数据是(﹣2)8=256;
当输入数据是n时,输出的数据是 (﹣2)n.
故答案为:256;(﹣2)n.
【解答】解:若x为偶数,根据题意得:4x+13>75,
解得x>15.5,
所以此时x的最小整数值为16;
若x为奇数,根据题意得:5x>75,
解得x>15,
所以此时x的最小整数值为17,
综上,输入的最小正整数x是16.
故答案为:16.
【解答】解:∵27m=(33)m=33m,9n=(32)n=32n,=,
∴=,
∴33m﹣2n==3﹣1,
∴3m﹣2n=﹣1,
故答案为:﹣1.
【解答】解:
=(x2+2xy+y2)
=(x+y)2.
当x+y=6时,
原式=×62
=×36
=18.
故答案为:18.
.【解答】解:∵A=B,a≠0,≠0,
∴=0,=1,|a|=a或=0,=a,|a|=1,
∴b=0,a=1(舍去)或b=0,a=﹣1,
∴b﹣a=0﹣(﹣1)=1,
故答案为:1.
三.解答题
【解答】解:(1)由题意得,长方形中空白部分的面积为:
ab﹣1×a﹣1×b+1×1
=ab﹣a﹣b+1;
(2)当 a=3,b=2时,
ab﹣a﹣b+1
=3×2﹣3﹣2+1
=2,
则长方形中空白部分的面积为2.
【解答】解:∵a+b=1,ab=﹣3.
∴a2+b2=(a+b)2﹣2ab=1﹣2×(﹣3)=7,
(1)=;
(2)===.
【解答】解:(1)∵x=﹣2<3,
∴M=+1=1+1=2,
故答案为:2;
(2)∵M=15,
∴+1=15(x≤3)或x2﹣x+3=15(x>3),
解得x=﹣28或x=4,
∴输入的x的值为﹣28或4,
故答案为:﹣28或4.
【解答】解:(1)休息区的面积为:×π×a2=a2(m2);
游泳区的面积为:3a×2a=6a2(m2).
故答案为:a2,6a2;
(2)∵长方形游乐场的宽为40米,
∴a=10米.
所以(6a×4a﹣6a2﹣a2)×30
≈(24a2﹣6a2﹣1.57a2)×30
=16.43a2×30
=492.9a2.
当a=10时,
原式=49290(元).
答:游乐场中绿化草地的费用为49290元.
.【解答】解:(1)方案A:40×5+40×50%x=20x+200,
方案B:40×60%(5+x)=24x+120;
(2)当x=50时,
20x+200
=20×50+200
=1200(元),
24x+120
=24×50+120
=1320(元),
∵1200<1320,
∴选择A方案更为优惠.
一.选择题
.已知a﹣2b2=3,则2022﹣2a+4b2的值是( )
A.2016 B.2028 C.2019 D.2025
.若x2﹣3x﹣2=0,则2x2﹣6x+2018的值为( )
A.2021 B.2022 C.2023 D.2024
.若x,y二者满足等式x2﹣2x=2y﹣y2,且xy=,则式子x2+2xy+y2﹣2(x+y)+2020的值为( )
A.2019 B.2020 C.2021 D.2022
.已知,当x=2时,ax3+bx+c的值是2022;当x=﹣2时,ax3+bx﹣c的值是( )
A.﹣2022 B.﹣2018 C.2018 D.2022
.如图是一个运算程序,能使输出结果m的值为6的是( )
A.x=1,y=2 B.x=﹣2,y=﹣2 C.x=2,y=1 D.x=3,y=﹣1
.当x=1时,代数式ax2﹣2bx+1的值为3,那么5﹣2a+4b的值是( )
A.1 B.2 C.3 D.4
.已知(x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,将x=0代入这个等式中可以求出a0=1.用这种方法可以求得a6+a5+a4+a3+a2+a1的值为( )
A.﹣16 B.16 C.﹣1 D.1
.下列关于代数式﹣m+1的值的结论:①﹣m+1的值可能是正数;②﹣m+1的值一定比﹣m大;③﹣m+1的值一定比1小;④﹣m+1的值随着m的增大而减小.其中所有正确结论的序号是( )
A.①②③ B.②③④ C.①②④ D.①③④
.已知关于x的多项式(m+3)x3﹣xn+x﹣mn为二次三项式,则当x=﹣1时,这个二次三项式的值是( )
A.7 B.6 C.4 D.3
.当x=1时,代数式px3+qx+1的值是﹣2020,则当x=﹣1时,代数式px3+qx+1的值是( )
A.2019 B.2020 C.2021 D.2022
二.填空题
.小王利用计算机设计了一个计算程序,输入和输出的数据如表:
输入 … 1 2 3 4 5 …
输出 … ﹣2 4 ﹣8 16 ﹣32 …
那么,当输入数据是8时,输出的数据是 ;当输入数据是n时,输出的数据是 .
12.如图,要使输出的y值大于75,则输入的最小正整数x是 .
13.若=,则2n﹣3m的值是 .
14.若x+y=6,则的值为 .
15.如M={1,2,x},我们叫集合M,其中1,2,x叫做集合M的元素.集合中的元素具有确定性(如x必然存在),互异性(如x≠1,x≠2),无序性(即改变元素的顺序,集合不变).若集合N={x,1,2},我们说M=N.已知集合A={1,0,a},集合B={,|a|,},若A=B,则b﹣a的值是 .
三.解答题
16.如图是一个长为a、宽为b的长方形,两个阴影图形都是一对底边长为1、且底边在长方形对边上的平行四边形.
(1)用含字母a,b的代数式表示长方形中空白部分的面积.
(2)当a=3,b=2时,求长方形中空白部分的面积.
17.已知a+b=1,ab=﹣3.求下列代数式的值:
(1);
(2).
18.某校数学社团设计了一个如图所示的数值转换程序.
(1)当输入x=﹣2时,输出M的值为 ;
(2)当输出M=15时,输入x的值为 .
19.如图是一个长方形游乐场,其宽是4a米,长是6a米.其中半圆形休息区和长方形游泳区以外的地方都是绿地.已知半圆形休息区的直径和长方形游泳区的宽是2a米,游泳区的长是3a米.
(1)该游乐场休息区的面积为 m2,游泳区的面积为 m2.(用含有a的式子表示)
(2)若长方形游乐场的宽为40米,绿化草地每平方米需要费用30元,求这个游乐场中绿化草地的费用.
20.某中学八年级(1)班5名老师决定带领本班x名学生去迁西景忠山旅游参观.该景区每张门票的票价为40元,现有A、B两种购票方案可供选择:方案A:教师全价,学生半价;方案B:不分教师与学生,全部六折优惠.
(1)请用含x的代数式分别表示选择A,B两种方案所需的费用;
(2)当学生人数x=50时,且只选择其中一种方案购票,请通过计算说明选择哪种方案更为优惠.
参考答案与试题解析
一.选择题
.【解答】解:2022﹣2a+4b2=2022﹣2(a﹣2b2),
∵a﹣2b2=3,
∴原式=2022﹣2×3=2016.
故选:A.
.【解答】解:∵x2﹣3x﹣2=0,
∴x2﹣3x=2,
∴2x2﹣6x+2018
=2(x2﹣3x)+2018
=2×2+2018
=4+2018
=2022,
故选:B.
.【解答】解:∵x2﹣2x=2y﹣y2,xy=
∴x2﹣2x+y2﹣2y=0,2xy=1.
∴x2+2xy+y2﹣2(x+y)+2020
=x2+2xy+y2﹣2x﹣2y+2020
=x2﹣2x+y2﹣2y+2xy+2020.
=0+1+2020
=2021.
故选:C.
.【解答】解:∵当x=2时,代数式ax3+bx+c的值为2022,
∴8a+2b=2022﹣c,
当x=﹣2时,
ax3﹣bx+3
=﹣8a﹣2b﹣c
=﹣(8a+2b)﹣c
=﹣2022+c﹣c
=﹣2022,
故选:A.
.【解答】解:∵选项A、C的y满足y≥0,把x、y的值代入m=x2﹣3y,
则选项A、C输出的值m分别为﹣5、1;
选项B、D的y满足y≤0,把x、y的值代入m=x2+3y,
则选项B、D输出的值m分别为10、6.
∴选项A、B、C都不满足输出m的值为6的条件,
选项D满足输出m的值为6的条件.
故选:D.
.【解答】解:根据题意,将x=1代入ax2﹣2bx+1=3,得:a﹣2b=2,
则5﹣2a+4b=﹣2(a﹣2b)+5=﹣2×2+5=﹣4+5=1.
故选:A.
.【解答】解:当x=1时,∵(x﹣1)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,
∴a6+a5+a4+a3+a2+a1+a0=0.
∴a6+a5+a4+a3+a2+a1=﹣a0=﹣1.
故选:C.
.【解答】解:当m=0时,﹣m+1=1>0,故①符合题意;
∵﹣m+1﹣(﹣m)=1>0,
∴﹣m+1>﹣m,故②符合题意;
当m=0时,﹣m+1=1,故③不符合题意;
m越大,﹣m越小,﹣m+1越小,故④符合题意;
故选:C.
.【解答】解:∵关于x的多项式(m+3)x3﹣xn+x﹣mn为二次三项式,
∴m+3=0,n=2,
解得:m=﹣3,
∴关于x的多项式为﹣x2+x+6,
当x=﹣1时,
原式=﹣(﹣1)2+(﹣1)+6
=﹣1﹣1+6
=4,
故选:C.
.【解答】解:∵x=1时,代数式px3+qx+1的值是﹣2020,
∴把x=1代入px3+qx+1得,
p+q+1=﹣2020,
∴p+q=﹣2021,
∴﹣p﹣q=2021,
把x=﹣1代入px3+qx+1得,
﹣p﹣q+1
=2021+1
=2022,
故选:D.
二.填空题
【解答】解:设输入数据为a,输出数据为b,
当a=1时,b=﹣2=(﹣2)1,
当a=2时,b=4=(﹣2)2,
当a=3时,b=﹣8=(﹣2)3,
,
∴b=(﹣2)a,
∴当输入数据是8时,输出的数据是(﹣2)8=256;
当输入数据是n时,输出的数据是 (﹣2)n.
故答案为:256;(﹣2)n.
【解答】解:若x为偶数,根据题意得:4x+13>75,
解得x>15.5,
所以此时x的最小整数值为16;
若x为奇数,根据题意得:5x>75,
解得x>15,
所以此时x的最小整数值为17,
综上,输入的最小正整数x是16.
故答案为:16.
【解答】解:∵27m=(33)m=33m,9n=(32)n=32n,=,
∴=,
∴33m﹣2n==3﹣1,
∴3m﹣2n=﹣1,
故答案为:﹣1.
【解答】解:
=(x2+2xy+y2)
=(x+y)2.
当x+y=6时,
原式=×62
=×36
=18.
故答案为:18.
.【解答】解:∵A=B,a≠0,≠0,
∴=0,=1,|a|=a或=0,=a,|a|=1,
∴b=0,a=1(舍去)或b=0,a=﹣1,
∴b﹣a=0﹣(﹣1)=1,
故答案为:1.
三.解答题
【解答】解:(1)由题意得,长方形中空白部分的面积为:
ab﹣1×a﹣1×b+1×1
=ab﹣a﹣b+1;
(2)当 a=3,b=2时,
ab﹣a﹣b+1
=3×2﹣3﹣2+1
=2,
则长方形中空白部分的面积为2.
【解答】解:∵a+b=1,ab=﹣3.
∴a2+b2=(a+b)2﹣2ab=1﹣2×(﹣3)=7,
(1)=;
(2)===.
【解答】解:(1)∵x=﹣2<3,
∴M=+1=1+1=2,
故答案为:2;
(2)∵M=15,
∴+1=15(x≤3)或x2﹣x+3=15(x>3),
解得x=﹣28或x=4,
∴输入的x的值为﹣28或4,
故答案为:﹣28或4.
【解答】解:(1)休息区的面积为:×π×a2=a2(m2);
游泳区的面积为:3a×2a=6a2(m2).
故答案为:a2,6a2;
(2)∵长方形游乐场的宽为40米,
∴a=10米.
所以(6a×4a﹣6a2﹣a2)×30
≈(24a2﹣6a2﹣1.57a2)×30
=16.43a2×30
=492.9a2.
当a=10时,
原式=49290(元).
答:游乐场中绿化草地的费用为49290元.
.【解答】解:(1)方案A:40×5+40×50%x=20x+200,
方案B:40×60%(5+x)=24x+120;
(2)当x=50时,
20x+200
=20×50+200
=1200(元),
24x+120
=24×50+120
=1320(元),
∵1200<1320,
∴选择A方案更为优惠.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
