5.3.1解方程(一)(教学设计)-五年级上册数学人教版
文档属性
| 名称 | 5.3.1解方程(一)(教学设计)-五年级上册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 218.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 00:00:00 | ||
图片预览




文档简介
《3.1-解方程(一)》教学设计
备课解决方案
备教材内容
1.本课时教学的是教材67~68页的内容。
2.例1通过天平保持平衡的原理来帮助解方程,并以x+3=9为例,讨论形如x±a=b的方程的解法。例2以3x=18为例,讨论形如ax=b(a≠0)的方程的解法。例3以20-x=9为例,讨论形如a±x=b的方程的解法。教材借助天平演示,引导学生根据天平保持平衡的原理,类推出解方程的方法。通过水果精灵的提示,引导学生进行检验、讨论和总结解方程的思路、解题步骤和注意事项。
3.例1以x十3=9为例,讨论了形如x士a=b的方程的解法。教学的重点是运用等式性质1解方程,并引入方程的解与解方程两个概念。为了便于给出解方程全过程的直观图示,例题中的数据比较小。教材借助三幅天平演示图,展现了解方程的完整思考过程,然后以此为例引入方程的解与解方程的概念。最后,提示还需要检验,并介绍验算过程。“方程的解”中的“解”是名词,指能使方程左右两边相等的未知数的值;“解方程”中的“解”是动词,指求方程的解的过程。对于学生来说,只要初步理解这两个概念的含义,能正确运用就行了,不必在概念叙述上过于咬文爵字。“做一做”安排了两题。第1题是解形如x士a=b的方程,
第2题是检验方程的解。
4.本课时学习的内容,既包括解方程的概念和解方程的依据,又包括方程的解法和应用,是进一步学习稍复杂方程的解法的基础。
备教法学法
学生已经掌握了方程的意义及等式的性质,教师可以在此基础上先复习等式的性质,再出示例题,并用天平表示,引导学生直接依据等式的性质进行转化,掌握解方程的方法,明确解题步骤和注意事项,提高学生的数学应用意识及自主探究的能力。引导学生运用等式性质。可采用思维定向的策略加以引导,即先复习等式性质1,出示例1并请学生口述方程后,再明确指出,从今天起我们将学习怎样根据等式性质来解方程。由于数据小,学生一眼就能看出x=6。为提高学习掌握新方法的积极性,教师还可强调这种思考方法以后到中学解更复杂的方程一直有用。为此,暂时避开算法多样化的讨论。注意培养学生的自学能力。得到x=6后,它叫什么?怎样检验它是否正确?请学生看书自学。然后通过交流,明确两个概念,并小结检验的思路:代人原方程,看左右两边是否相等,这样做的依据,就是“方程的解”的意义。引导小结“做一做”的收获。第1题的三小题,共同点是:依据相同,都是等式性质1;思路相同,为了得到x=?(这是解方程的目标),都在等式两边加上或减去相同的数。小结这两点有利于凸显用等式性质解方程的优点:不用再去区分未知的是加数,还是被减数,也不用再去回忆它们各自的关系式第2题的小结,主要是启发学生体会代入检验是辩别方程的解的好方法。
备教学目标
1.经历解方程的过程,理解方程的解和解方程的意义。
2.能根据等式的性质解形如x士a=b、ax=b(a≠0)、x÷a=b(a≠0)、a-x=和a÷x=b的方程,培养运算能力。
3.能运用所学知识解决简单的实际问题,感受数学与现实生活的密切联系。
备教学重难点
重点:根据等式的性质解方程。
难点:掌握减数或除数是未知数的方程的解法。
备已学知识
1.方程的意义。
含有未知数的等式就是方程。
2.等式的性质。
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
备知识讲解
知识点一 形如x±a=b的方程的解法及方程的解和解方程的意义
问题导入 看图列方程,并求出x的值。(教材67页例1)
过程讲解
1.根据图意列出方程
(1)看图、理解图意,并找出题中的等量关系。
从图中可知:盒子里面有x个球,盒子外面有3个球,一共有9个球。
由此可以得出题中的等量关系:盒子里面球的个数(x个)+盒子外面球的个数(3个)=球的总个数(9个)。
(2)列出方程。
x+3=9
2.探究x+3=9的解法
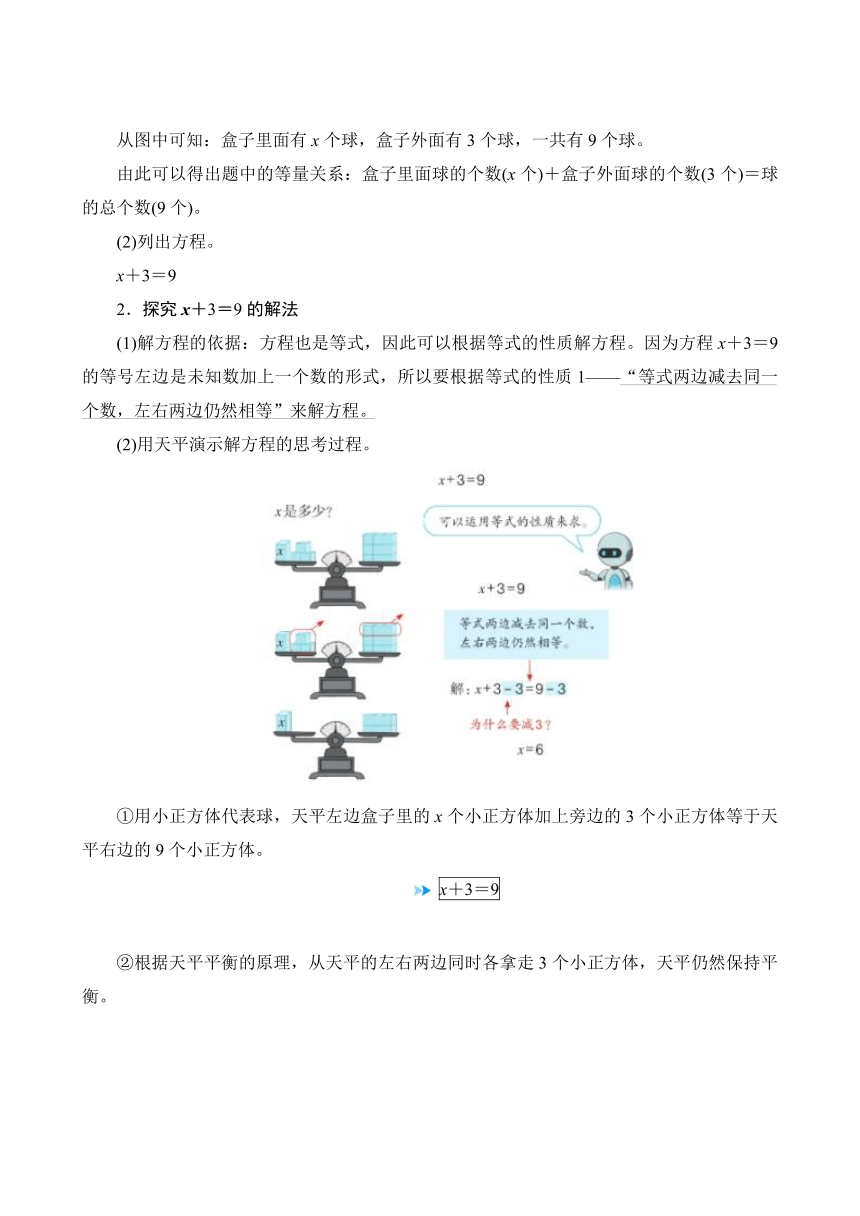
(1)解方程的依据:方程也是等式,因此可以根据等式的性质解方程。因为方程x+3=9的等号左边是未知数加上一个数的形式,所以要根据等式的性质1——“等式两边减去同一个数,左右两边仍然相等”来解方程。
(2)用天平演示解方程的思考过程。
①用小正方体代表球,天平左边盒子里的x个小正方体加上旁边的3个小正方体等于天平右边的9个小正方体。
x+3=9
②根据天平平衡的原理,从天平的左右两边同时各拿走3个小正方体,天平仍然保持平衡。
根据等式的性质1,方程左右两边同时减去3,左右两边仍然相等,即x+3-3=9-3。
③天平左边盒子里的小正方体的个数等于天平右边剩下的小正方体的个数。
x=6
3.书写格式
x+3=9
书写格式 在解方程之前必须先写“解”字。解方程时注意书写格式,等号上、下要对齐。
解: x+3-3=9-3
x=6
4.明确方程的解和解方程的意义
(1)使方程左右两边相等的未知数的值,叫做方程的解。
如x=6就是方程x+3=9的解。
(2)求方程的解的过程叫做解方程。
重点提示 “方程的解”中的“解”是名词,指使方程左右两边相等的未知数的值;“解方程”中的“解”是动词,指求方程的解的过程。
5.检验
判断x=6是不是方程x+3=9的解,可以检验。
把x=6代入方程。
方程左边=x+3
=6+3
=9
方法提示 在检验的过程中,如果方程左边=方程右边,那么这个解是方程的解,否则就不是方程的解。
=方程右边
所以,x=6是方程的解。
6.问题拓展:形如x-a=b的方程的解法
形如x-a=b的方程的解法与形如x+a=b的方程的解法基本相同。
根据等式的性质1,方程左右两边同时加上1.8,左右两边仍然相等。
例如:x-1.8=4
解:x-1.8+1.8=4+1.8
x=5.8
归纳总结
1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.根据等式的性质1可以解形如x±a=b的方程。
4.形如x±a=b的方程的解法:
x+a=b
解:x+a-a=b-a
x=b-a
x-a=b
解:x-a+a=b+a
x=b+a
5.判断一个方程解得是否正确,可以把未知数的值代入原方程中进行检验。
知识点二 形如ax=b(a≠0)和x÷a=b(a≠0)的方程的解法
问题导入 解方程3x=18。(教材68页例2)
过程讲解
1.探究3x=18的解法
(1)解方程的依据:因为方程3x=18的等号左边是未知数与一个数相乘的形式,所以要根据等式的性质2——“等式两边除以同一个不为0的数,左右两边仍然相等”来解方程。
(2)用天平演示解方程的思考过程。
①用一个大长方体代表x,天平左边的3个大长方体等于天平右边的18个小长方体。
3x=18
②把天平左右两边的长方体都平均分成3份,根据天平平衡的原理,天平的左右两边都留下其中的1份,天平仍然保持平衡。
根据等式的性质2,方程左右两边同时除以3,左右两边仍然相等,即3x÷3=18÷3,求得x=6。
2.书写格式
3x=18
解:3x÷3=18÷3
x=6
3.检验
把x=6代入方程,
方程左边=3x
=3×6
=18
=方程右边
所以,x=6是方程的解。
4.问题拓展:形如x÷a=b(a≠0)的方程的解法
形如x÷a=b(a≠0)的方程的解法与形如ax=b(a≠0)的方程的解法基本相同。
例如:
根据等式的性质2,方程左右两边同时乘7,左右两边仍然相等。
x÷7=0.3
解:x÷7×7=0.3×7
x=2.1
归纳总结
1.根据等式的性质2可以解形如ax=b(a≠0)和x÷a=b(a≠0)的方程。
2.形如ax=b(a≠0)和x÷a=b(a≠0)的方程的解法:
ax=b
解:ax÷a=b÷a
x=b÷a
x÷a=b
解:x÷a×a=b×a
x=b×a
知识点三 形如a-x=b的方程的解法
问题导入 解方程20-x=9。(教材68页例3)
过程讲解
1.解方程的依据
根据等式的性质1,先把原方程中的“-x”转化为“+x”,再解方程。
2.解方程20-x=9的过程及其书写格式
3.检验
把x=11代入方程,
重点提示 通过检验能判断方程的解是否正确,因此解完方程后要进行检验。
方程左边=20-x
=20-11
=9
=方程右边
所以,x=11是方程的解。
归纳总结
解形如a-x=b的方程时,可以根据等式的性质1,先在方程左右两边同时加上x,使其转化为形如a+x=b的方程,再求出x的值。
知识点四 形如a÷x=b的方程的解法
问题导入 解方程2.1÷x=3。(教材68页“做一做”)
过程讲解
1.解方程的依据
根据等式的性质2,先在方程左右两边同时乘x,使其转化为形如ax=b(a≠0)的方程,再求出x的值。
2.解方程2.1÷x=3的过程及其书写格式
归纳总结
解形如a÷x=b的方程时,可以根据等式的性质2,先在方程左右两边同时乘x,使其转化为形如ax=b(a≠0)的方程,再求出x的值。
备易错易混
误区一 判断:方程的解就是解方程。(√)
错解分析 方程的解是一个数值,解方程是一个计算过程。
错解改正 ×
温馨提示
“方程的解”和“解方程”是两个不同的概念。
误区二 解方程x-16=24。
x-16=24
解:x-16+16=24+24
x=48
错解分析 根据等式的性质1,方程左右两边应该同时加上16,而本题中方程左边加上16,右边却加上24,导致计算结果错误。
错解改正
x-16=24
解:x-16+16=24+16
x=40
温馨提示
运用等式的性质1解方程时,方程左右两边应该加上或减去同一个数,而不是加上或减去方程左右两边各自的数。
备综合能力
方法运用 运用代入法解决稍复杂的方程问题
典型例题 方程x+1.2=10.1与mx=21.36有相同的解,求m的值。
思路分析
两个方程的解相同,也就是x的值相同。
求出方程x+1.2=10.1的解。
把求出的x的值代入mx=21.36中,得到一个新方程。
求出新方程的解,即m的值。
正确解答
x+1.2=10.1
解:x+1.2-1.2=10.1-1.2
x=8.9
把x=8.9代入m x,=21.36中,可得:
8.9m=21.36
解:8.9m÷8.9=21.36÷8.9
m=2.4
答:m的值是2.4。
方法总结
解决此类方程问题时,可先求出其中一个隐含在已知条件中的未知数的值,再求出另一个未知数的值。
综合运用 运用等式各部分之间的关系比较方程中字母所代表数值的大小
典型例题 不计算,把下面每组方程中代表数值最大的字母圈出来。
(1) A+20=100 B+30=100
C+40=100 D+50=100
(2)A-20=100 B-30=100
C-40=100 D-50=100
(3)20A=100 30B=100
40C=100 50D=100
(4)A÷20=100 B÷30=100
C÷40=100 D÷50=100
思路分析 根据和、差、积、商相等时,加数与加数、被减数与减数、因数与因数、被除数与除数之间的关系解决问题。
(1)和相等时,已知加数越小,未知加数越大。
(2)差相等时,减数越大,被减数越大。
(3)积相等时,已知因数越小,未知因数越大。
(4)商相等时,除数越大,被除数越大。
正确解答
方法总结
在此类问题中,加法与乘法的变化规律类似,减法与除法的变化规律类似。
备教学资源
猜谜语
谜语:解方程,猜灯谜。(打一成语)
谜底:寻根究底。
趣味歌谣中的方程
古代的劳动人民创造了许多形式新颖、独特、朗朗上口、饶有兴趣的数学诗,下面列举一道能用一元一次方程求解的数学诗,供同学们赏析。
俺院里,有群鸡,加上七,减去七,
乘上七,除去七,其结果,仍是七,
你算算,多少鸡?
正确解答 解:设院里有x只鸡。
[(x+7)-7]×7÷7=7
x=7
答:院里有7只鸡。
备课解决方案
备教材内容
1.本课时教学的是教材67~68页的内容。
2.例1通过天平保持平衡的原理来帮助解方程,并以x+3=9为例,讨论形如x±a=b的方程的解法。例2以3x=18为例,讨论形如ax=b(a≠0)的方程的解法。例3以20-x=9为例,讨论形如a±x=b的方程的解法。教材借助天平演示,引导学生根据天平保持平衡的原理,类推出解方程的方法。通过水果精灵的提示,引导学生进行检验、讨论和总结解方程的思路、解题步骤和注意事项。
3.例1以x十3=9为例,讨论了形如x士a=b的方程的解法。教学的重点是运用等式性质1解方程,并引入方程的解与解方程两个概念。为了便于给出解方程全过程的直观图示,例题中的数据比较小。教材借助三幅天平演示图,展现了解方程的完整思考过程,然后以此为例引入方程的解与解方程的概念。最后,提示还需要检验,并介绍验算过程。“方程的解”中的“解”是名词,指能使方程左右两边相等的未知数的值;“解方程”中的“解”是动词,指求方程的解的过程。对于学生来说,只要初步理解这两个概念的含义,能正确运用就行了,不必在概念叙述上过于咬文爵字。“做一做”安排了两题。第1题是解形如x士a=b的方程,
第2题是检验方程的解。
4.本课时学习的内容,既包括解方程的概念和解方程的依据,又包括方程的解法和应用,是进一步学习稍复杂方程的解法的基础。
备教法学法
学生已经掌握了方程的意义及等式的性质,教师可以在此基础上先复习等式的性质,再出示例题,并用天平表示,引导学生直接依据等式的性质进行转化,掌握解方程的方法,明确解题步骤和注意事项,提高学生的数学应用意识及自主探究的能力。引导学生运用等式性质。可采用思维定向的策略加以引导,即先复习等式性质1,出示例1并请学生口述方程后,再明确指出,从今天起我们将学习怎样根据等式性质来解方程。由于数据小,学生一眼就能看出x=6。为提高学习掌握新方法的积极性,教师还可强调这种思考方法以后到中学解更复杂的方程一直有用。为此,暂时避开算法多样化的讨论。注意培养学生的自学能力。得到x=6后,它叫什么?怎样检验它是否正确?请学生看书自学。然后通过交流,明确两个概念,并小结检验的思路:代人原方程,看左右两边是否相等,这样做的依据,就是“方程的解”的意义。引导小结“做一做”的收获。第1题的三小题,共同点是:依据相同,都是等式性质1;思路相同,为了得到x=?(这是解方程的目标),都在等式两边加上或减去相同的数。小结这两点有利于凸显用等式性质解方程的优点:不用再去区分未知的是加数,还是被减数,也不用再去回忆它们各自的关系式第2题的小结,主要是启发学生体会代入检验是辩别方程的解的好方法。
备教学目标
1.经历解方程的过程,理解方程的解和解方程的意义。
2.能根据等式的性质解形如x士a=b、ax=b(a≠0)、x÷a=b(a≠0)、a-x=和a÷x=b的方程,培养运算能力。
3.能运用所学知识解决简单的实际问题,感受数学与现实生活的密切联系。
备教学重难点
重点:根据等式的性质解方程。
难点:掌握减数或除数是未知数的方程的解法。
备已学知识
1.方程的意义。
含有未知数的等式就是方程。
2.等式的性质。
等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
备知识讲解
知识点一 形如x±a=b的方程的解法及方程的解和解方程的意义
问题导入 看图列方程,并求出x的值。(教材67页例1)
过程讲解
1.根据图意列出方程
(1)看图、理解图意,并找出题中的等量关系。
从图中可知:盒子里面有x个球,盒子外面有3个球,一共有9个球。
由此可以得出题中的等量关系:盒子里面球的个数(x个)+盒子外面球的个数(3个)=球的总个数(9个)。
(2)列出方程。
x+3=9
2.探究x+3=9的解法
(1)解方程的依据:方程也是等式,因此可以根据等式的性质解方程。因为方程x+3=9的等号左边是未知数加上一个数的形式,所以要根据等式的性质1——“等式两边减去同一个数,左右两边仍然相等”来解方程。
(2)用天平演示解方程的思考过程。
①用小正方体代表球,天平左边盒子里的x个小正方体加上旁边的3个小正方体等于天平右边的9个小正方体。
x+3=9
②根据天平平衡的原理,从天平的左右两边同时各拿走3个小正方体,天平仍然保持平衡。
根据等式的性质1,方程左右两边同时减去3,左右两边仍然相等,即x+3-3=9-3。
③天平左边盒子里的小正方体的个数等于天平右边剩下的小正方体的个数。
x=6
3.书写格式
x+3=9
书写格式 在解方程之前必须先写“解”字。解方程时注意书写格式,等号上、下要对齐。
解: x+3-3=9-3
x=6
4.明确方程的解和解方程的意义
(1)使方程左右两边相等的未知数的值,叫做方程的解。
如x=6就是方程x+3=9的解。
(2)求方程的解的过程叫做解方程。
重点提示 “方程的解”中的“解”是名词,指使方程左右两边相等的未知数的值;“解方程”中的“解”是动词,指求方程的解的过程。
5.检验
判断x=6是不是方程x+3=9的解,可以检验。
把x=6代入方程。
方程左边=x+3
=6+3
=9
方法提示 在检验的过程中,如果方程左边=方程右边,那么这个解是方程的解,否则就不是方程的解。
=方程右边
所以,x=6是方程的解。
6.问题拓展:形如x-a=b的方程的解法
形如x-a=b的方程的解法与形如x+a=b的方程的解法基本相同。
根据等式的性质1,方程左右两边同时加上1.8,左右两边仍然相等。
例如:x-1.8=4
解:x-1.8+1.8=4+1.8
x=5.8
归纳总结
1.使方程左右两边相等的未知数的值,叫做方程的解。
2.求方程的解的过程叫做解方程。
3.根据等式的性质1可以解形如x±a=b的方程。
4.形如x±a=b的方程的解法:
x+a=b
解:x+a-a=b-a
x=b-a
x-a=b
解:x-a+a=b+a
x=b+a
5.判断一个方程解得是否正确,可以把未知数的值代入原方程中进行检验。
知识点二 形如ax=b(a≠0)和x÷a=b(a≠0)的方程的解法
问题导入 解方程3x=18。(教材68页例2)
过程讲解
1.探究3x=18的解法
(1)解方程的依据:因为方程3x=18的等号左边是未知数与一个数相乘的形式,所以要根据等式的性质2——“等式两边除以同一个不为0的数,左右两边仍然相等”来解方程。
(2)用天平演示解方程的思考过程。
①用一个大长方体代表x,天平左边的3个大长方体等于天平右边的18个小长方体。
3x=18
②把天平左右两边的长方体都平均分成3份,根据天平平衡的原理,天平的左右两边都留下其中的1份,天平仍然保持平衡。
根据等式的性质2,方程左右两边同时除以3,左右两边仍然相等,即3x÷3=18÷3,求得x=6。
2.书写格式
3x=18
解:3x÷3=18÷3
x=6
3.检验
把x=6代入方程,
方程左边=3x
=3×6
=18
=方程右边
所以,x=6是方程的解。
4.问题拓展:形如x÷a=b(a≠0)的方程的解法
形如x÷a=b(a≠0)的方程的解法与形如ax=b(a≠0)的方程的解法基本相同。
例如:
根据等式的性质2,方程左右两边同时乘7,左右两边仍然相等。
x÷7=0.3
解:x÷7×7=0.3×7
x=2.1
归纳总结
1.根据等式的性质2可以解形如ax=b(a≠0)和x÷a=b(a≠0)的方程。
2.形如ax=b(a≠0)和x÷a=b(a≠0)的方程的解法:
ax=b
解:ax÷a=b÷a
x=b÷a
x÷a=b
解:x÷a×a=b×a
x=b×a
知识点三 形如a-x=b的方程的解法
问题导入 解方程20-x=9。(教材68页例3)
过程讲解
1.解方程的依据
根据等式的性质1,先把原方程中的“-x”转化为“+x”,再解方程。
2.解方程20-x=9的过程及其书写格式
3.检验
把x=11代入方程,
重点提示 通过检验能判断方程的解是否正确,因此解完方程后要进行检验。
方程左边=20-x
=20-11
=9
=方程右边
所以,x=11是方程的解。
归纳总结
解形如a-x=b的方程时,可以根据等式的性质1,先在方程左右两边同时加上x,使其转化为形如a+x=b的方程,再求出x的值。
知识点四 形如a÷x=b的方程的解法
问题导入 解方程2.1÷x=3。(教材68页“做一做”)
过程讲解
1.解方程的依据
根据等式的性质2,先在方程左右两边同时乘x,使其转化为形如ax=b(a≠0)的方程,再求出x的值。
2.解方程2.1÷x=3的过程及其书写格式
归纳总结
解形如a÷x=b的方程时,可以根据等式的性质2,先在方程左右两边同时乘x,使其转化为形如ax=b(a≠0)的方程,再求出x的值。
备易错易混
误区一 判断:方程的解就是解方程。(√)
错解分析 方程的解是一个数值,解方程是一个计算过程。
错解改正 ×
温馨提示
“方程的解”和“解方程”是两个不同的概念。
误区二 解方程x-16=24。
x-16=24
解:x-16+16=24+24
x=48
错解分析 根据等式的性质1,方程左右两边应该同时加上16,而本题中方程左边加上16,右边却加上24,导致计算结果错误。
错解改正
x-16=24
解:x-16+16=24+16
x=40
温馨提示
运用等式的性质1解方程时,方程左右两边应该加上或减去同一个数,而不是加上或减去方程左右两边各自的数。
备综合能力
方法运用 运用代入法解决稍复杂的方程问题
典型例题 方程x+1.2=10.1与mx=21.36有相同的解,求m的值。
思路分析
两个方程的解相同,也就是x的值相同。
求出方程x+1.2=10.1的解。
把求出的x的值代入mx=21.36中,得到一个新方程。
求出新方程的解,即m的值。
正确解答
x+1.2=10.1
解:x+1.2-1.2=10.1-1.2
x=8.9
把x=8.9代入m x,=21.36中,可得:
8.9m=21.36
解:8.9m÷8.9=21.36÷8.9
m=2.4
答:m的值是2.4。
方法总结
解决此类方程问题时,可先求出其中一个隐含在已知条件中的未知数的值,再求出另一个未知数的值。
综合运用 运用等式各部分之间的关系比较方程中字母所代表数值的大小
典型例题 不计算,把下面每组方程中代表数值最大的字母圈出来。
(1) A+20=100 B+30=100
C+40=100 D+50=100
(2)A-20=100 B-30=100
C-40=100 D-50=100
(3)20A=100 30B=100
40C=100 50D=100
(4)A÷20=100 B÷30=100
C÷40=100 D÷50=100
思路分析 根据和、差、积、商相等时,加数与加数、被减数与减数、因数与因数、被除数与除数之间的关系解决问题。
(1)和相等时,已知加数越小,未知加数越大。
(2)差相等时,减数越大,被减数越大。
(3)积相等时,已知因数越小,未知因数越大。
(4)商相等时,除数越大,被除数越大。
正确解答
方法总结
在此类问题中,加法与乘法的变化规律类似,减法与除法的变化规律类似。
备教学资源
猜谜语
谜语:解方程,猜灯谜。(打一成语)
谜底:寻根究底。
趣味歌谣中的方程
古代的劳动人民创造了许多形式新颖、独特、朗朗上口、饶有兴趣的数学诗,下面列举一道能用一元一次方程求解的数学诗,供同学们赏析。
俺院里,有群鸡,加上七,减去七,
乘上七,除去七,其结果,仍是七,
你算算,多少鸡?
正确解答 解:设院里有x只鸡。
[(x+7)-7]×7÷7=7
x=7
答:院里有7只鸡。
