冀教版数学九年级上册 28.1 圆的概念及性质教案(表格式)
文档属性
| 名称 | 冀教版数学九年级上册 28.1 圆的概念及性质教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 14:14:39 | ||
图片预览


文档简介
28.1 圆的概念及性质
┃教学整体设计┃
【教学目标】
1.能在图形中准确识别圆、圆心、半径、直径、圆弧、半圆、等圆、等弧等;认识圆的对称性,知道圆既是轴对称图形,又是中心对称图形.
2.经历观察、动手操作;抽象和建立圆的概念、探究圆的对称性及相关性质的过程,熟记圆及有关概念.
3.培养学生动手意识,体会数学与生活实际的联系,体验成功的乐趣.体会在解决问题的过程中与他人合作的重要性,培养合作精神.
【重点难点】
重点:圆的概念及应用,揭示与圆有关的本质属性对称性.
难点:圆的概念及其表示方法.
┃教学过程设计┃
教学过程 设计意图
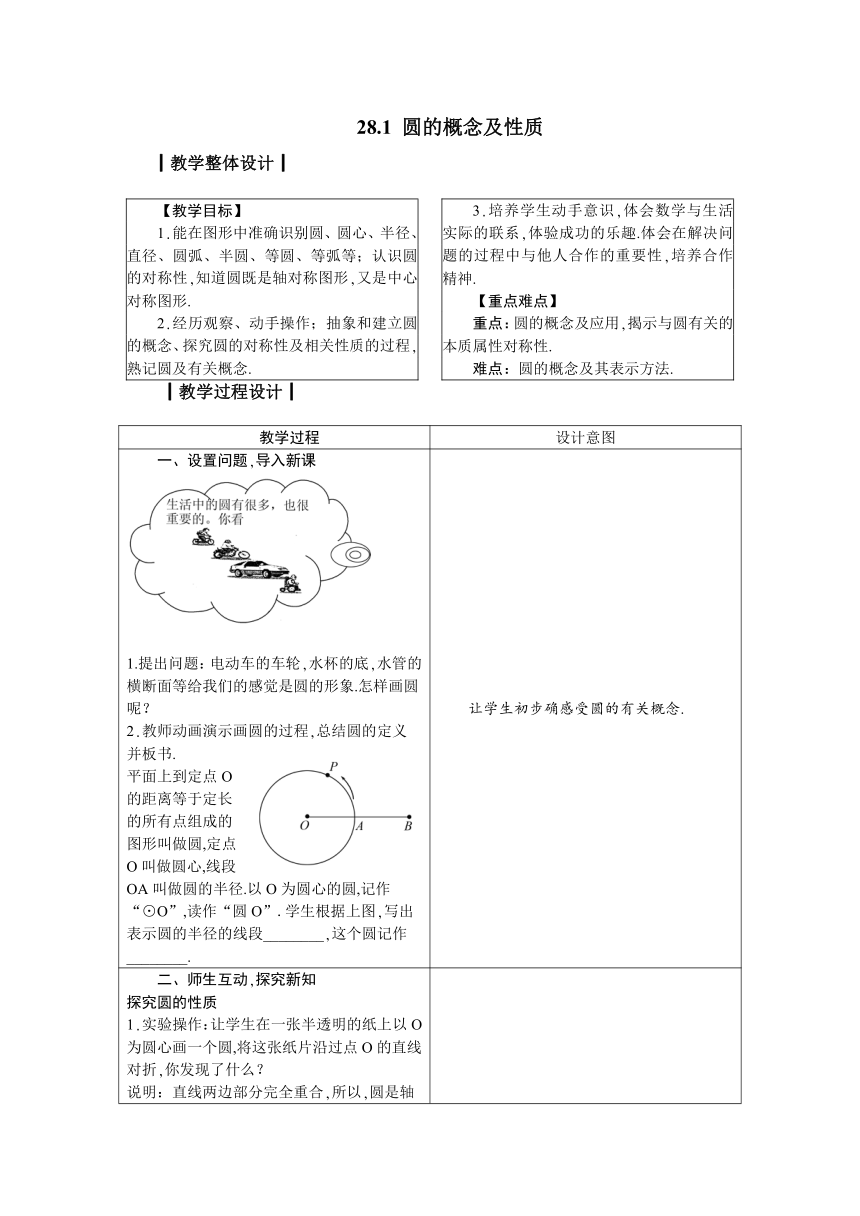
一、设置问题,导入新课 1.提出问题:电动车的车轮,水杯的底,水管的横断面等给我们的感觉是圆的形象.怎样画圆呢? 2.教师动画演示画圆的过程,总结圆的定义并板书. 平面上到定点O的距离等于定长的所有点组成的图形叫做圆,定点O叫做圆心,线段OA叫做圆的半径.以O为圆心的圆,记作“⊙O”,读作“圆O”.学生根据上图,写出表示圆的半径的线段________,这个圆记作________. 让学生初步确感受圆的有关概念.
二、师生互动,探究新知 探究圆的性质 1.实验操作:让学生在一张半透明的纸上以O为圆心画一个圆,将这张纸片沿过点O的直线对折,你发现了什么? 说明:直线两边部分完全重合,所以,圆是轴对称图形,过圆心的直线是它的一条对称轴. 2.提问:圆有多少条对称轴?这些对称轴的共同特征是什么? 说明:圆有无数条对称轴,这些对称轴的共同特征是都过圆心. 3.提问:将一个圆绕圆心旋转180°后,是否与原图形重合?这能说明什么事实? 说明:圆是中心对称图形. 结论:圆是轴对称图形,过圆心的每一条直线都是对称轴.圆也是中心对称图形,圆心是它的对称中心. 师生活动:学生动手操作,在动手中感受图的对称,教师巡回指导. 探究圆相关概念 1.弦和直径. 指出:连接圆上任意两点的线段叫做弦. 如图,线段BC叫做⊙O的弦. 进一步指出:图中弦AB经过圆心O,我们把经过圆心的弦叫做这个圆的直径.最后让学生观察,得出:直径等于半径的2倍. 2.弧的概念. 继续观察图,发现,连接圆上任意两个点可以得到一条弦同时,这两个点还将圆分成两部分,我们把每一部分叫做圆弧,即圆上任意两点间的部分叫做圆弧,简称弧.用符号“⌒”表示,如以B,C为端点的弧,记作__________.继续引导学生观察会发现,圆的任意一条直径的两个端点分圆成两条弧,每一条弧我们把它叫做半圆;大于半圆的弧叫做优弧,如图中______,______等,小于半圆的弧叫做劣弧,如图中______,______等. 3.等圆. 能够完全重合的两个圆叫做等圆,半径相等的两个圆是等圆.(用投影或电脑演示圆重合的过程) 4.等弧. 电脑或投影演示两段弧重合的过程,指出:在同圆或等圆中,能够互相重合的弧叫做等弧. 师生活动:师生一起观察图形,认知概念. 精讲解疑 概念辨析: 1.直径是弦,弦是直径.这句话正确吗?(学生口答,并说明理由) 教师强调:直径是弦,但在一般情况下弦不是直径,只有在弦经过圆心时,弦才叫做直径. 2.半圆是弧吗?弧是不是半圆?(学生口答,并说明理由) 教师强调:半圆是弧,但在一般情况下弧不是半圆,只有直径的两个端点分圆成的两条弧才是半圆. 3.长度相等的两条弧是等弧吗?为什么?(学生口答) 教师强调:长度相等的弧不一定是等弧,等弧必须是在同圆或等圆中的弧.(教师用两要根长度相等的铁丝,变成弧度不同的两条弧加以比较,此难点很容易被突破) 师生活动:通过师生共同探究,辨析圆的概念间的联系与区别. 让学生通过动手自己体会圆的对称性,在获取知识和经验. 能过师生共同探究,进一步明晰概念,让学生分析概念间的联系与区别.
三、运用新知,解决问题 1.以点O为圆心,可以作几个圆( ) A.只能1个 B.2个 C.3个 D.无数个 2.在同一平面内与已知点O的距离等于3cm的所有点组成的图形是______. 3.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF. 求证:AF=BE.
四、课堂小结,提炼观点 1.本节课学习了什么内容? 2.从数学方法上主要学习了什么?
五、布置作业,巩固提升 必做:教材第148页A组第1,2题. 选做:教材第149页B组第1,2题.
┃教学小结┃
【板书设计】
圆的概念及性质
1.圆的概念
2.圆的性质
3.圆的相关概念
【教学反思】
本节课概念较多,学生学习结合图形记忆更好,数形结合思想一定要求学生应用.
┃教学整体设计┃
【教学目标】
1.能在图形中准确识别圆、圆心、半径、直径、圆弧、半圆、等圆、等弧等;认识圆的对称性,知道圆既是轴对称图形,又是中心对称图形.
2.经历观察、动手操作;抽象和建立圆的概念、探究圆的对称性及相关性质的过程,熟记圆及有关概念.
3.培养学生动手意识,体会数学与生活实际的联系,体验成功的乐趣.体会在解决问题的过程中与他人合作的重要性,培养合作精神.
【重点难点】
重点:圆的概念及应用,揭示与圆有关的本质属性对称性.
难点:圆的概念及其表示方法.
┃教学过程设计┃
教学过程 设计意图
一、设置问题,导入新课 1.提出问题:电动车的车轮,水杯的底,水管的横断面等给我们的感觉是圆的形象.怎样画圆呢? 2.教师动画演示画圆的过程,总结圆的定义并板书. 平面上到定点O的距离等于定长的所有点组成的图形叫做圆,定点O叫做圆心,线段OA叫做圆的半径.以O为圆心的圆,记作“⊙O”,读作“圆O”.学生根据上图,写出表示圆的半径的线段________,这个圆记作________. 让学生初步确感受圆的有关概念.
二、师生互动,探究新知 探究圆的性质 1.实验操作:让学生在一张半透明的纸上以O为圆心画一个圆,将这张纸片沿过点O的直线对折,你发现了什么? 说明:直线两边部分完全重合,所以,圆是轴对称图形,过圆心的直线是它的一条对称轴. 2.提问:圆有多少条对称轴?这些对称轴的共同特征是什么? 说明:圆有无数条对称轴,这些对称轴的共同特征是都过圆心. 3.提问:将一个圆绕圆心旋转180°后,是否与原图形重合?这能说明什么事实? 说明:圆是中心对称图形. 结论:圆是轴对称图形,过圆心的每一条直线都是对称轴.圆也是中心对称图形,圆心是它的对称中心. 师生活动:学生动手操作,在动手中感受图的对称,教师巡回指导. 探究圆相关概念 1.弦和直径. 指出:连接圆上任意两点的线段叫做弦. 如图,线段BC叫做⊙O的弦. 进一步指出:图中弦AB经过圆心O,我们把经过圆心的弦叫做这个圆的直径.最后让学生观察,得出:直径等于半径的2倍. 2.弧的概念. 继续观察图,发现,连接圆上任意两个点可以得到一条弦同时,这两个点还将圆分成两部分,我们把每一部分叫做圆弧,即圆上任意两点间的部分叫做圆弧,简称弧.用符号“⌒”表示,如以B,C为端点的弧,记作__________.继续引导学生观察会发现,圆的任意一条直径的两个端点分圆成两条弧,每一条弧我们把它叫做半圆;大于半圆的弧叫做优弧,如图中______,______等,小于半圆的弧叫做劣弧,如图中______,______等. 3.等圆. 能够完全重合的两个圆叫做等圆,半径相等的两个圆是等圆.(用投影或电脑演示圆重合的过程) 4.等弧. 电脑或投影演示两段弧重合的过程,指出:在同圆或等圆中,能够互相重合的弧叫做等弧. 师生活动:师生一起观察图形,认知概念. 精讲解疑 概念辨析: 1.直径是弦,弦是直径.这句话正确吗?(学生口答,并说明理由) 教师强调:直径是弦,但在一般情况下弦不是直径,只有在弦经过圆心时,弦才叫做直径. 2.半圆是弧吗?弧是不是半圆?(学生口答,并说明理由) 教师强调:半圆是弧,但在一般情况下弧不是半圆,只有直径的两个端点分圆成的两条弧才是半圆. 3.长度相等的两条弧是等弧吗?为什么?(学生口答) 教师强调:长度相等的弧不一定是等弧,等弧必须是在同圆或等圆中的弧.(教师用两要根长度相等的铁丝,变成弧度不同的两条弧加以比较,此难点很容易被突破) 师生活动:通过师生共同探究,辨析圆的概念间的联系与区别. 让学生通过动手自己体会圆的对称性,在获取知识和经验. 能过师生共同探究,进一步明晰概念,让学生分析概念间的联系与区别.
三、运用新知,解决问题 1.以点O为圆心,可以作几个圆( ) A.只能1个 B.2个 C.3个 D.无数个 2.在同一平面内与已知点O的距离等于3cm的所有点组成的图形是______. 3.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF. 求证:AF=BE.
四、课堂小结,提炼观点 1.本节课学习了什么内容? 2.从数学方法上主要学习了什么?
五、布置作业,巩固提升 必做:教材第148页A组第1,2题. 选做:教材第149页B组第1,2题.
┃教学小结┃
【板书设计】
圆的概念及性质
1.圆的概念
2.圆的性质
3.圆的相关概念
【教学反思】
本节课概念较多,学生学习结合图形记忆更好,数形结合思想一定要求学生应用.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
