1.3.2三角形全等的条件ASA与AAS 课件(共16张PPT) 2023—2024学年鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 1.3.2三角形全等的条件ASA与AAS 课件(共16张PPT) 2023—2024学年鲁教版(五四制)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 16:15:05 | ||
图片预览





文档简介
(共16张PPT)
1.3.2探索三角形全等的条件(2)
回顾与思考:
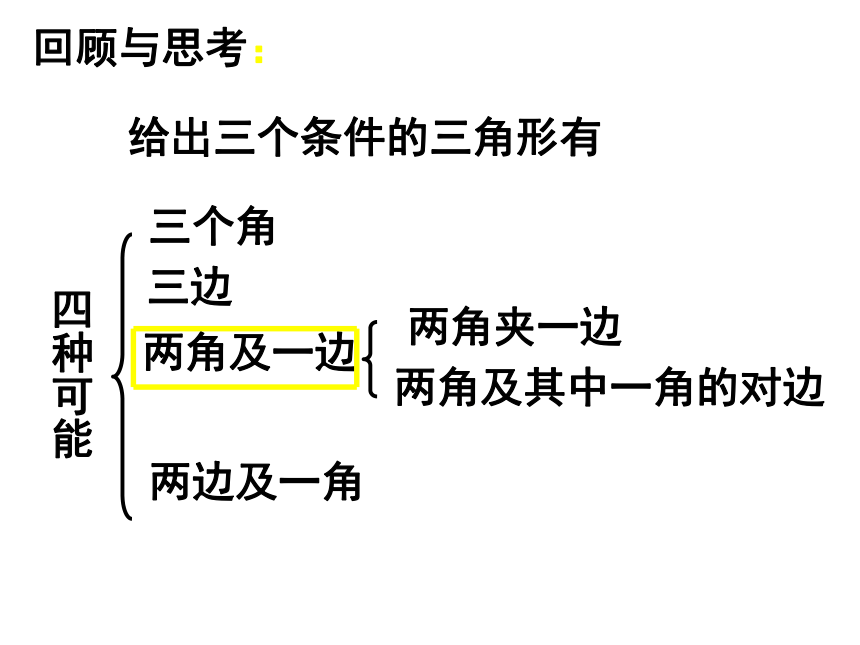
给出三个条件的三角形有
四种可能
三个角
两边及一角
两角及一边
三边
两角夹一边
两角及其中一角的对边
一、提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
A
B
C
D
E
F
两角和它们的夹边对应相等的两个三角形全等.简写成“角边角”或“ASA”
练一练
观察下面三个三角形,哪两个三角形是全等三角形?
R
P
3
60
Q
40
A
B
C
3
40
60
F
E
D
3
40
60
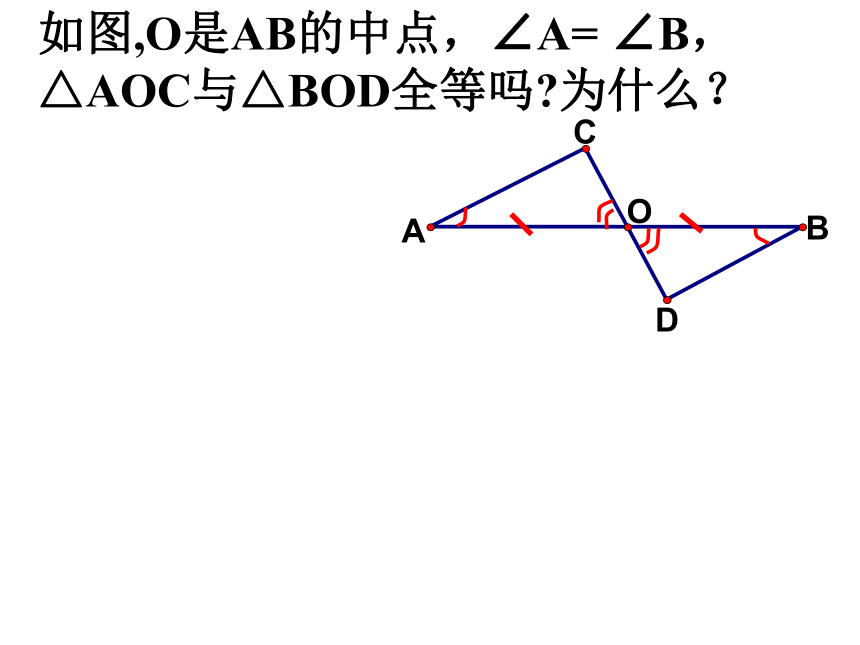
如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗 为什么?
O
A
B
C
D
【跟踪练习】1、如右图,D在AC上,E在AB上,AB=AC,∠B=∠C.求证:AD=AE,BE=CD
A
B
C
M
N
P
如图,在△ABC和△MNP中,∠A=∠M ,∠B=∠N,BC=NP.△ABC与△MNP全等吗?为什么?
两角和其中一个角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”
1、 图中的两个三角形全等吗 请说明理由.
35°
35°
110°
110°
A
B
C
D
DBC
ABC
D
≌
D
\
练一练:
(已知)
(已知)
(公共边)
2、已知:如图,∠1=∠2,∠C=∠D。求证:AC=AD。
不全等,因为BC虽然是公共边,但不是对应边。
1.已知:∠ABC= ∠CDB
∠ACB= ∠CDB 那么△ABC≌ △CDB吗?为什么
(3) 如图,D是线段BE的中点,∠C=∠A,∠B=∠E,请在图中找出一对全等三角形.
并说明理由。
B
A
C
D
E
拓展提高
如图,海岸上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么点A到海岛C的距离与点B到海岛D的距离相等,为什么?
3、点E、F在线段BF上,BE=CF,AB∥DE,∠ACB=∠F。求证:△ABC≌△DEF
A
B
C
D
E
F
练习:
练习1 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证: △ABE≌△ACD
(ASA)
∴ △ABE ≌△ACD
(已知)
AB=AC
∠B=∠C
∠A= ∠A
(公共角)
证明:∵在△ABE与△ACD中
(已知)
AE=AD
目标检测:
1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF
2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
A
B
C
D
E
F
∠B=∠E或∠A=∠D
C
A
B
1
2
E
D
1.3.2探索三角形全等的条件(2)
回顾与思考:
给出三个条件的三角形有
四种可能
三个角
两边及一角
两角及一边
三边
两角夹一边
两角及其中一角的对边
一、提出问题:小明不小心将一块三角形模具打碎了,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具呢?如果可以,带哪块去合适?
A
B
C
D
E
F
两角和它们的夹边对应相等的两个三角形全等.简写成“角边角”或“ASA”
练一练
观察下面三个三角形,哪两个三角形是全等三角形?
R
P
3
60
Q
40
A
B
C
3
40
60
F
E
D
3
40
60
如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗 为什么?
O
A
B
C
D
【跟踪练习】1、如右图,D在AC上,E在AB上,AB=AC,∠B=∠C.求证:AD=AE,BE=CD
A
B
C
M
N
P
如图,在△ABC和△MNP中,∠A=∠M ,∠B=∠N,BC=NP.△ABC与△MNP全等吗?为什么?
两角和其中一个角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”
1、 图中的两个三角形全等吗 请说明理由.
35°
35°
110°
110°
A
B
C
D
DBC
ABC
D
≌
D
\
练一练:
(已知)
(已知)
(公共边)
2、已知:如图,∠1=∠2,∠C=∠D。求证:AC=AD。
不全等,因为BC虽然是公共边,但不是对应边。
1.已知:∠ABC= ∠CDB
∠ACB= ∠CDB 那么△ABC≌ △CDB吗?为什么
(3) 如图,D是线段BE的中点,∠C=∠A,∠B=∠E,请在图中找出一对全等三角形.
并说明理由。
B
A
C
D
E
拓展提高
如图,海岸上有A、B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么点A到海岛C的距离与点B到海岛D的距离相等,为什么?
3、点E、F在线段BF上,BE=CF,AB∥DE,∠ACB=∠F。求证:△ABC≌△DEF
A
B
C
D
E
F
练习:
练习1 已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC,∠B=∠C。
求证: △ABE≌△ACD
(ASA)
∴ △ABE ≌△ACD
(已知)
AB=AC
∠B=∠C
∠A= ∠A
(公共角)
证明:∵在△ABE与△ACD中
(已知)
AE=AD
目标检测:
1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF
2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
A
B
C
D
E
F
∠B=∠E或∠A=∠D
C
A
B
1
2
E
D
