1.3.1探索三角形全等的条件(SSS)课件(共33张PPT) 2023—2024学年鲁教版(五四制)数学七年级上册
文档属性
| 名称 | 1.3.1探索三角形全等的条件(SSS)课件(共33张PPT) 2023—2024学年鲁教版(五四制)数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 885.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 16:13:40 | ||
图片预览









文档简介
(共33张PPT)
1.3.1探索三角形全等的条件
A
B
C
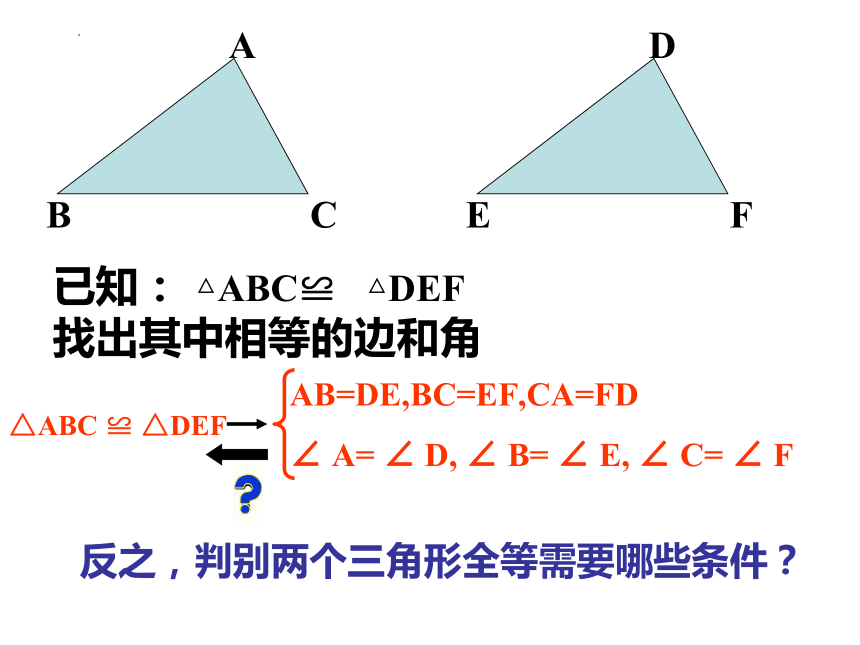
已知: △ABC≌ △DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
D
E
F
AB=DE,BC=EF,CA=FD
∠ A= ∠ D, ∠ B= ∠ E, ∠ C= ∠ F
△ABC ≌ △DEF
学习目标
1.经历探索三角形全等“边边边”的条件过程,掌握并会应用“边边边”说明两个三角形全等;
2.了解三角形的稳定性.
一、只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
只给一个角时
如:
45°
45°
45°
二、只给一个条件(一条边或一个角)
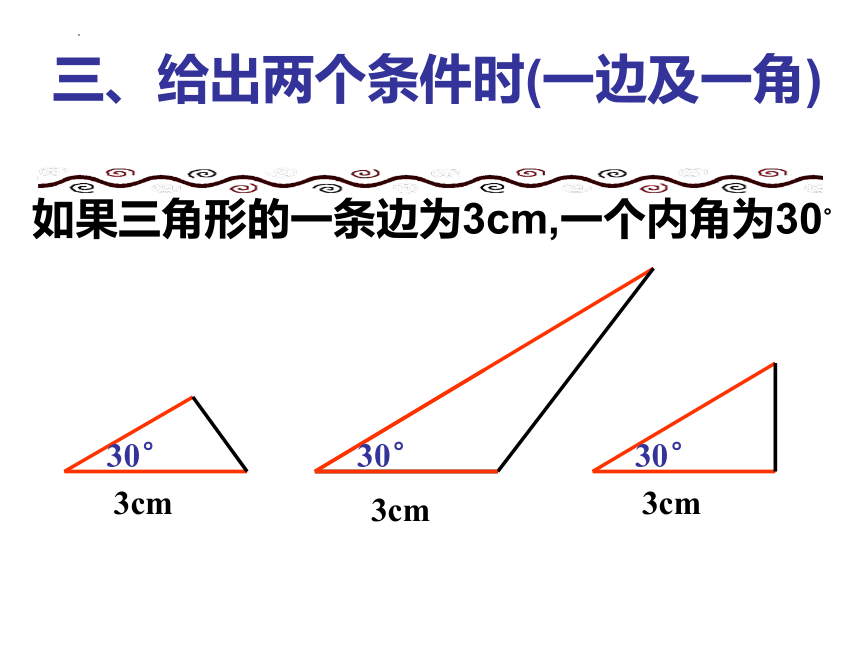
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
三、给出两个条件时(一边及一角)
四、给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
五、给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm 时
6cm
4cm
4cm
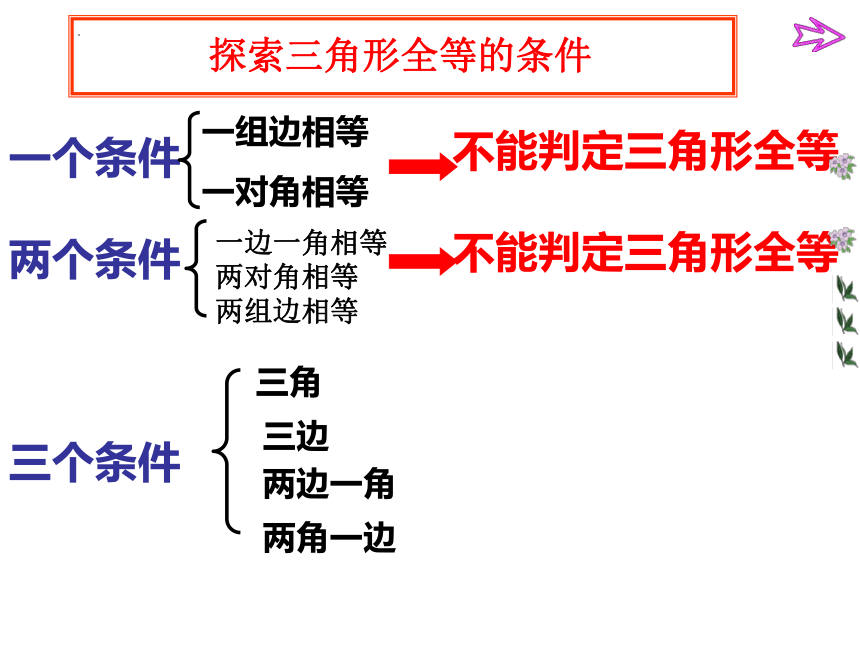
一个条件
不能判定三角形全等
三个条件
三边
三角
两角一边
两边一角
两个条件
一组边相等
一对角相等
不能判定三角形全等
一边一角相等
两对角相等
两组边相等
探索三角形全等的条件
如果三角形两个内角分别为30°,45°时,
第三角是多少度?
30°
45°
30°
45°
三个内角分别相等的两个三角形不一定全等。
六、给出三个条件时(已知三角)
105°
105°
七、给出三个条件时(已知三边)
(2)用三根长度分别为4cm,5cm,7cm的木棒摆一个三角形,把你摆出的三角形与同伴摆出的进行比较,它们一定全等吗
三边分别相等的两个三角形全等。
简写为“边边边”或“SSS”
知识点一:
由上面的结论可知:只要三角形的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性.这种性质表现为判定三角形全等的条件SSS,与角无关
三角形的稳定性
三角形具有稳定性
四边形不具有
生活中有许多利用用三角形的稳定性制成的东西
请看下面几组图片
工人师傅造门时,常用木条EF固定矩形门框ABCD如图,使其不变形,这种做法的根据是 ﹙ ﹚
A 两点之间线段最短 B 矩形的对称性
C 矩形的四个角都是直角 D 三角形的稳定性
A
D
F
E
B
--
D
c
学以致用
A
B
C
A
B
C
三边分别相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
例1.如图,△ABC中 AB=AC, D为BC中点
求证:①△ABD≌△ACD. ②∠BAD=∠CAD ③AD⊥BC
例2 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC
A
B
C
D
AC
AC
AB=AD
BC=CD
∴ △ABC ≌ △ADC(SSS)
证明:在△ABC和△ADC中
=
(已知)
(已知)
(公共边)
例2 已知:如图,AB=AD,BC=CD,
求证:AC平分∠BAD
A
B
C
D
AC
AC
AB=AD
BC=CD
∴ △ABC≌△ADC(SSS)
证明:在△ABC和△ADC中
=
(已知)
(已知)
(公共边)
∴∠BAC=∠DAC,∴AC平分∠BAD
你还能得出其它结论吗?
例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A= ∠ C (全等三角形的对应角相等)
变式:已知AB=CD,AD=CB,求证:∠B=∠D
证明:连接AC,
AB=CD(已知)
AC=AC(公共边)
BC=AD(已知)
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
在△ABC和△ ADC中
归纳:
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤:
先写出在哪两个三角形中;
摆出三个条件用大括号括起来;
写出全等结论。
证明全等的书写步骤:
这节课你学到了什么?
三边对应相等的两个三角形全等,简写成“边边边”或“SSS”
三角形的稳定性
注意:要充分利用图形中“对顶角相等,公共角,公共边”这些条件.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
课堂感悟
练习1.如图:B、D、C、F四点在同一直线上,AB=EF,AC=ED,BD=FC, ①△ABC与△EFD是否全等?为什么?②AB∥EF吗?
A
B
C
D
E
F
解:①∵BD=CF
∴BD+DC=CF+DC
即BC=DF
在△ABC和△DEF中
AB=EF
AC=DE ② 由①得△ABC≌△DEF
BC=DF ∴∠B=∠F
∴ △ABC≌△DEF ∴AB∥EF
当堂检测:
1.如图,已知AC=DB,要使△ABC≌△DCB,由“SSS” 可知只需再补充条件( )
A、BC=CB B、OB=OC
C、AB=DC D、AB=BD
2.如图,ΔABC中,AB=AC,BE=EC,则由“SSS”可判定( )
A.ΔABD≌ΔACD
B、ΔABE≌ΔACE
C.ΔBED≌ΔCED
D、以上答案都不对
1.3.1探索三角形全等的条件
A
B
C
已知: △ABC≌ △DEF
找出其中相等的边和角
反之,判别两个三角形全等需要哪些条件?
D
E
F
AB=DE,BC=EF,CA=FD
∠ A= ∠ D, ∠ B= ∠ E, ∠ C= ∠ F
△ABC ≌ △DEF
学习目标
1.经历探索三角形全等“边边边”的条件过程,掌握并会应用“边边边”说明两个三角形全等;
2.了解三角形的稳定性.
一、只给一个条件(一条边或一个角)
只给一条边时
如:
3cm
3cm
3cm
只给一个角时
如:
45°
45°
45°
二、只给一个条件(一条边或一个角)
如果三角形的一条边为3cm,一个内角为30°
3cm
3cm
3cm
30°
30°
30°
三、给出两个条件时(一边及一角)
四、给出两个条件时(已知两角)
如果三角形两个内角分别为30°,45°时
30°
45°
30°
45°
30°
45°
五、给出两个条件时(已知两边)
如果三角形的两边分别为4cm,6cm 时
6cm
4cm
4cm
一个条件
不能判定三角形全等
三个条件
三边
三角
两角一边
两边一角
两个条件
一组边相等
一对角相等
不能判定三角形全等
一边一角相等
两对角相等
两组边相等
探索三角形全等的条件
如果三角形两个内角分别为30°,45°时,
第三角是多少度?
30°
45°
30°
45°
三个内角分别相等的两个三角形不一定全等。
六、给出三个条件时(已知三角)
105°
105°
七、给出三个条件时(已知三边)
(2)用三根长度分别为4cm,5cm,7cm的木棒摆一个三角形,把你摆出的三角形与同伴摆出的进行比较,它们一定全等吗
三边分别相等的两个三角形全等。
简写为“边边边”或“SSS”
知识点一:
由上面的结论可知:只要三角形的长度确定了,这个三角形的形状和大小就完全确定了,三角形的这个性质叫做三角形的稳定性.这种性质表现为判定三角形全等的条件SSS,与角无关
三角形的稳定性
三角形具有稳定性
四边形不具有
生活中有许多利用用三角形的稳定性制成的东西
请看下面几组图片
工人师傅造门时,常用木条EF固定矩形门框ABCD如图,使其不变形,这种做法的根据是 ﹙ ﹚
A 两点之间线段最短 B 矩形的对称性
C 矩形的四个角都是直角 D 三角形的稳定性
A
D
F
E
B
--
D
c
学以致用
A
B
C
A
B
C
三边分别相等的两个三角形全等.
(简写成“边边边”或“SSS”)
如何用符号语言来表达呢
≌
结论
例1.如图,△ABC中 AB=AC, D为BC中点
求证:①△ABD≌△ACD. ②∠BAD=∠CAD ③AD⊥BC
例2 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC
A
B
C
D
AC
AC
AB=AD
BC=CD
∴ △ABC ≌ △ADC(SSS)
证明:在△ABC和△ADC中
=
(已知)
(已知)
(公共边)
例2 已知:如图,AB=AD,BC=CD,
求证:AC平分∠BAD
A
B
C
D
AC
AC
AB=AD
BC=CD
∴ △ABC≌△ADC(SSS)
证明:在△ABC和△ADC中
=
(已知)
(已知)
(公共边)
∴∠BAC=∠DAC,∴AC平分∠BAD
你还能得出其它结论吗?
例3:如图,在四边形ABCD中,AB=CD,AD=CB,求证:∠ A= ∠ C.
D
A
B
C
证明:在△ABD和△CDB中
AB=CD
AD=CB
BD=DB
∴△ABD≌△ACD(SSS)
(已知)
(已知)
(公共边)
∴ ∠ A= ∠ C (全等三角形的对应角相等)
变式:已知AB=CD,AD=CB,求证:∠B=∠D
证明:连接AC,
AB=CD(已知)
AC=AC(公共边)
BC=AD(已知)
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
A
B
C
D
A
B
C
D
在△ABC和△ ADC中
归纳:
①准备条件:证全等时要用的条件要先证好;
②三角形全等书写三步骤:
先写出在哪两个三角形中;
摆出三个条件用大括号括起来;
写出全等结论。
证明全等的书写步骤:
这节课你学到了什么?
三边对应相等的两个三角形全等,简写成“边边边”或“SSS”
三角形的稳定性
注意:要充分利用图形中“对顶角相等,公共角,公共边”这些条件.
判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。
课堂感悟
练习1.如图:B、D、C、F四点在同一直线上,AB=EF,AC=ED,BD=FC, ①△ABC与△EFD是否全等?为什么?②AB∥EF吗?
A
B
C
D
E
F
解:①∵BD=CF
∴BD+DC=CF+DC
即BC=DF
在△ABC和△DEF中
AB=EF
AC=DE ② 由①得△ABC≌△DEF
BC=DF ∴∠B=∠F
∴ △ABC≌△DEF ∴AB∥EF
当堂检测:
1.如图,已知AC=DB,要使△ABC≌△DCB,由“SSS” 可知只需再补充条件( )
A、BC=CB B、OB=OC
C、AB=DC D、AB=BD
2.如图,ΔABC中,AB=AC,BE=EC,则由“SSS”可判定( )
A.ΔABD≌ΔACD
B、ΔABE≌ΔACE
C.ΔBED≌ΔCED
D、以上答案都不对
