12.1 全等三角形 课件(共26张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 12.1 全等三角形 课件(共26张PPT)【2023秋人教八上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 20:38:30 | ||
图片预览








文档简介
(共26张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十二章 全等三角形
12.1 全等三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形的性质并会运用.
学习目标
重点
重点
下图所示的例子中都有形状、大小相同的图形.你能再举出一些类似的例子吗?
新课引入
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗 把三角尺和裁得的纸板放在一起能够完全重合吗
探究
一 全等三角形的相关概念
形状、大小完全一样.
能够完全重合.
新知学习
从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗
能够完全重合.
可以看到,形状、大小相同的图形放在一起能够完全重合,能够完全重合的两个图形叫做全等形.
归纳
能够完全重合的两个三角形叫做全等三角形.
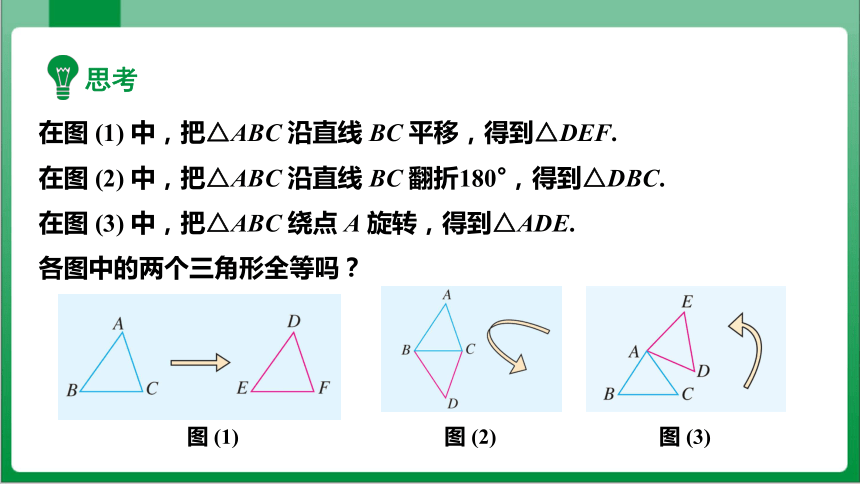
思考
在图 (1) 中,把△ABC 沿直线 BC 平移,得到△DEF.
在图 (2) 中,把△ABC 沿直线 BC 翻折180°,得到△DBC.
在图 (3) 中,把△ABC 绕点 A 旋转,得到△ADE.
各图中的两个三角形全等吗?
图 (1)
图 (3)
图 (2)
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
图 (1)
图 (3)
图 (2)
D
E
F
A
B
C
把两个全等的三角形重合到一起,
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角.
如图,△ABC 和△DEF 全等,
对应顶点:点 A 和点 D,点 B 和点 E,点 C 和点 F ;
对应边:AB 和 DE,BC 和 EF,AC 和 DF;
对应角:∠A 和∠D,∠B 和∠E,∠C 和∠F .
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
D
E
F
A
B
C
△ABC 和△DEF 全等,记做△ABC ≌△DEF .
全等用符号“≌”表示,读作“全等于”.
例1 说出图 (2)(3) 中两个全等三角形的对应顶点、对应边和对应角,并写成△***≌△***的形式.
图 (2)
△ABC≌△DBC.
对应顶点:点 A 和点 D,点 B 和点 B,点 C 和点 C ;
对应边:AB 和 DB,BC 和 BC,AC 和 DC;
对应角:∠A 和∠D,∠ABC 和∠DBC,∠ACB 和∠DCB .
图 (3)
△ABC≌△ADE
对应顶点:点 A 和点 A,点 B 和点 D,点 C 和点 E ;
对应边:AB 和 AD,BC 和 DE,AC 和 AE;
对应角:∠A 和∠A,∠B 和∠D,∠C 和∠E .
二 全等三角形的性质
思考
如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
D
E
F
A
B
C
完全重合
全等三角形的对应边相等,
全等三角形的对应角相等 .
全等三角形的对应边相等,全等三角形的对应角相等 .
全等三角形的性质
符号语言:
∵△ABC≌△DEF,
∴AB=DE,BC=EF,CA=FD,
∠A=∠D,∠B=∠E,∠C=∠F.
归纳
A
B
C
F
D
E
例1 如图,△ABC≌△CDA,AB 和 CD,BC 和 DA 是对应边,写出其他对应边及对应角.
C
A
B
D
其他对应边:AC 与 CA ( 注意字母的顺序 )
对应角:∠BAC 与∠DCA,∠BCA 与∠DAC, ∠B 与∠D.
即使是同一条线段,对应端点不同,结果也是不同的含义.
归纳
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;最大角对最大角,最小角对最小角.
例2 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1 等于多少度?
利用全等三角形的性质求解
a
b
c
b
c
60°
54°
1
∠1 = 180°-54°-60°=66°.
针对训练
1. 如图,△ABN≌△ACM,∠B 和∠C 是对应角,AB 和 AC 是对应边.写出其他对应边及对应角.
C
B
A
M
N
对应边还有:AM 与 AN,BN 与 CM.
对应角:∠BAN 与∠CAM,∠AMC 与∠ANB.
解:对应边有: EF 和 NM,EG 和 NH;
对应角有:∠E 和∠N,∠F 和∠M,∠EGF 和∠NHM.
1.如图,△EFG≌△NMH,∠F 和∠M 是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.EF = 2.1 cm,EH = 1.1 cm,NH = 3.3 cm.
(1)写出其他对应边和对应角;
随堂练习
(2)求线段 NM 及 HG 的长度;
解:∵ △EFG≌△NMH,
∴ EF = NM = 2.1 cm,
EG = NH = 3.3 cm.
∴ HG = EG - EH = 3.3 - 1.1 = 2.2 (cm).
分析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
2. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.
46
全等
三角形
定义
能够完全重合的两个三角形
叫做全等三角形
基本性质
全等三角形对应边相等
全等三角形对应角相等
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十二章 全等三角形
12.1 全等三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.
3.掌握全等三角形的性质并会运用.
学习目标
重点
重点
下图所示的例子中都有形状、大小相同的图形.你能再举出一些类似的例子吗?
新课引入
把一块三角尺按在纸板上,画下图形,照图形裁下来的纸板和三角尺的形状、大小完全一样吗 把三角尺和裁得的纸板放在一起能够完全重合吗
探究
一 全等三角形的相关概念
形状、大小完全一样.
能够完全重合.
新知学习
从同一张底片冲洗出来的两张尺寸相同的照片上的图形,放在一起也能够完全重合吗
能够完全重合.
可以看到,形状、大小相同的图形放在一起能够完全重合,能够完全重合的两个图形叫做全等形.
归纳
能够完全重合的两个三角形叫做全等三角形.
思考
在图 (1) 中,把△ABC 沿直线 BC 平移,得到△DEF.
在图 (2) 中,把△ABC 沿直线 BC 翻折180°,得到△DBC.
在图 (3) 中,把△ABC 绕点 A 旋转,得到△ADE.
各图中的两个三角形全等吗?
图 (1)
图 (3)
图 (2)
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.
图 (1)
图 (3)
图 (2)
D
E
F
A
B
C
把两个全等的三角形重合到一起,
重合的顶点叫做对应顶点,
重合的边叫做对应边,
重合的角叫做对应角.
如图,△ABC 和△DEF 全等,
对应顶点:点 A 和点 D,点 B 和点 E,点 C 和点 F ;
对应边:AB 和 DE,BC 和 EF,AC 和 DF;
对应角:∠A 和∠D,∠B 和∠E,∠C 和∠F .
注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上.
D
E
F
A
B
C
△ABC 和△DEF 全等,记做△ABC ≌△DEF .
全等用符号“≌”表示,读作“全等于”.
例1 说出图 (2)(3) 中两个全等三角形的对应顶点、对应边和对应角,并写成△***≌△***的形式.
图 (2)
△ABC≌△DBC.
对应顶点:点 A 和点 D,点 B 和点 B,点 C 和点 C ;
对应边:AB 和 DB,BC 和 BC,AC 和 DC;
对应角:∠A 和∠D,∠ABC 和∠DBC,∠ACB 和∠DCB .
图 (3)
△ABC≌△ADE
对应顶点:点 A 和点 A,点 B 和点 D,点 C 和点 E ;
对应边:AB 和 AD,BC 和 DE,AC 和 AE;
对应角:∠A 和∠A,∠B 和∠D,∠C 和∠E .
二 全等三角形的性质
思考
如图,△ABC≌△DEF,对应边有什么关系?对应角呢?
D
E
F
A
B
C
完全重合
全等三角形的对应边相等,
全等三角形的对应角相等 .
全等三角形的对应边相等,全等三角形的对应角相等 .
全等三角形的性质
符号语言:
∵△ABC≌△DEF,
∴AB=DE,BC=EF,CA=FD,
∠A=∠D,∠B=∠E,∠C=∠F.
归纳
A
B
C
F
D
E
例1 如图,△ABC≌△CDA,AB 和 CD,BC 和 DA 是对应边,写出其他对应边及对应角.
C
A
B
D
其他对应边:AC 与 CA ( 注意字母的顺序 )
对应角:∠BAC 与∠DCA,∠BCA 与∠DAC, ∠B 与∠D.
即使是同一条线段,对应端点不同,结果也是不同的含义.
归纳
寻找全等三角形对应边、对应角的三种方法:
字母顺序法 根据书写规范,按照对应顶点确定对应边、对应角.
位置关系法 公共角(对顶角)为对应角,公共边为对应边;对应角的对边为对应边,对应边的对角为对应角.
图形特征法 最长边对最长边,最短边对最短边;最大角对最大角,最小角对最小角.
例2 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1 等于多少度?
利用全等三角形的性质求解
a
b
c
b
c
60°
54°
1
∠1 = 180°-54°-60°=66°.
针对训练
1. 如图,△ABN≌△ACM,∠B 和∠C 是对应角,AB 和 AC 是对应边.写出其他对应边及对应角.
C
B
A
M
N
对应边还有:AM 与 AN,BN 与 CM.
对应角:∠BAN 与∠CAM,∠AMC 与∠ANB.
解:对应边有: EF 和 NM,EG 和 NH;
对应角有:∠E 和∠N,∠F 和∠M,∠EGF 和∠NHM.
1.如图,△EFG≌△NMH,∠F 和∠M 是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.EF = 2.1 cm,EH = 1.1 cm,NH = 3.3 cm.
(1)写出其他对应边和对应角;
随堂练习
(2)求线段 NM 及 HG 的长度;
解:∵ △EFG≌△NMH,
∴ EF = NM = 2.1 cm,
EG = NH = 3.3 cm.
∴ HG = EG - EH = 3.3 - 1.1 = 2.2 (cm).
分析:先根据三角形外角的性质求出
∠ ACA'=∠A+∠B=27°+40°=67°.
再由△ABC绕点C按顺时针方向旋转至△A'B'C,得到△ABC≌△A'B'C,
∴∠ACB=∠A'CB'.
∴∠ACB–∠B'CA=∠A'CB'–∠B'CA, 即∠BCB'=∠ACA'=67°.
∴∠ACB'=180°–∠ACA'–∠BCB'=180°–67°–67°=46°.
2. 如图所示,将△ABC绕点C按顺时针方向旋转至△A'B'C,使点A'落在BC的延长线上.已知∠A=27°,∠B=40°,则∠ACB'为_______度.
46
全等
三角形
定义
能够完全重合的两个三角形
叫做全等三角形
基本性质
全等三角形对应边相等
全等三角形对应角相等
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
