12.2 三角形全等的判定第3课时用“ASA”或“AAS”判定三角形全等 课件(共28张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 12.2 三角形全等的判定第3课时用“ASA”或“AAS”判定三角形全等 课件(共28张PPT)【2023秋人教八上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 20:55:05 | ||
图片预览







文档简介
(共28张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十二章 全等三角形
第3课时 用“ASA”或“AAS”判定三角形全等
第2节 三角形全等的判定
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
学习目标
重点
重点
我们已经学习了哪些判定两个三角形全等的方法?
三个条件
④两角一边
③两边一角
②三边
①三角
不行
“边边边”或“SSS”
?
“边角边”或“SAS”
新课引入
思考
A
C
B
A'
C'
B'
A
C
B
A'
C'
B'
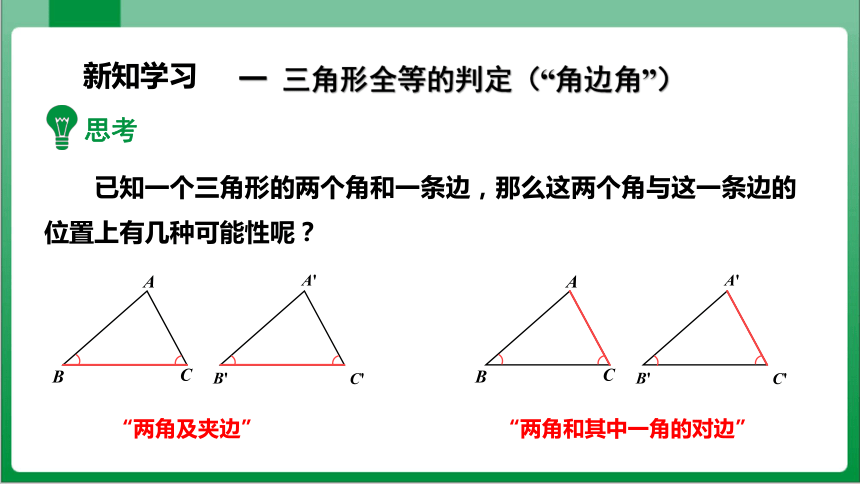
已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置上有几种可能性呢?
“两角及夹边”
“两角和其中一角的对边”
一 三角形全等的判定(“角边角”)
新知学习
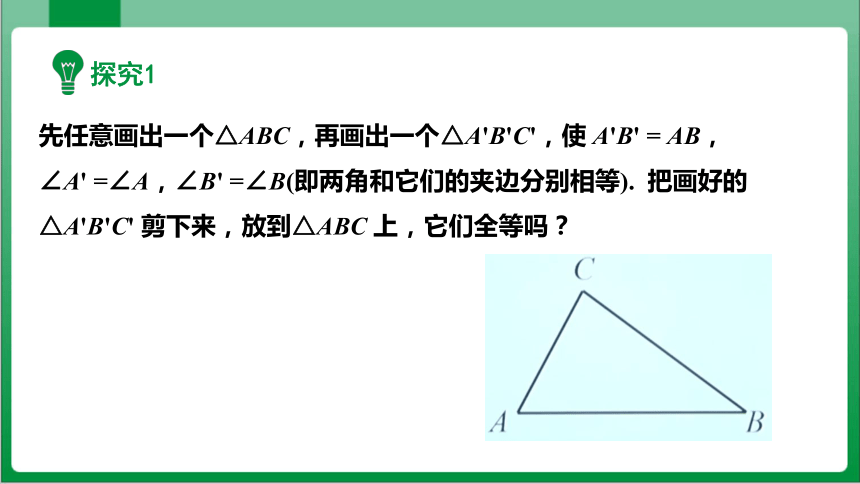
先任意画出一个△ABC,再画出一个△A'B'C',使 A'B' = AB,
∠A' =∠A,∠B' =∠B(即两角和它们的夹边分别相等). 把画好的△A'B'C' 剪下来,放到△ABC 上,它们全等吗?
探究1
画法:(1) 画 A'B' = AB;
(2) 在 A'B' 的同旁画∠DA'B' =∠A,∠EB'A' =∠B,A'D, B'E 相交于点 C'.
A
B
C
A'
B'
C'
E'
D'
如图,已知△ABC. 画一个△A'B'C',使A'B' = AB,∠A' =∠A,∠B' =∠B .
现象:两个三角形能完全重合.
说明:这两个三角形全等.
两角和它们的夹边分别相等的两个三角形全等. ( 可简写成“角边角”或“ASA”)
由探究1可以得到以下基本事实,用它可以判定两个三角形全等:
归纳
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
A'B' = AB
∴ △ABC ≌ △A'B'C' ( ASA )
A
B
C
A'
B'
C'
例1 如图,点 D 在 AB 上,点 E 在 AC 上,BA = AC,∠B =∠C.
求证:AE = AD.
目标: AE = AD
△ABE≌△ACD
A
D
B
E
C
证明:在△ABE 和△ACD 中,
∠B =∠C
AB = AC
∠A =∠A ( 公共角 )
∵△ABE ≌△ACD ( ASA )
∴AE = AD
A
D
B
E
C
例2 如图,在△ABC 和△A'B'C' 中,∠A' =∠A,∠B' =∠B,B'C' = BC. 求证:△A'B'C' ≌△ABC .
A
C
B
A'
C'
B'
分析:如果能证明∠C' =∠C,就可以利用“角边角”证明△ABC和△A'B'C' 全等.由三角形内角和定理可以证明∠C' =∠C.
二 三角形全等的判定(“角角边”)
证明:在△ABC 中,∠A +∠B +∠C = 180°,
∴∠C =180°- ∠A -∠B.
同理,∠C' = 180°-∠A' -∠B'.
∵∠A =∠A',∠B =∠B', ∴∠C =∠C'.
在△ ABC 与△A'B'C' 中,
∠C =∠C'
∵ BC = B'C',
∠B =∠B',
∴△ABC≌△A'B'C' (ASA)
A
C
B
A'
C'
B'
因此,我们可以得到下面的结论:
两角和其中一角的对边分别相等的两个三角形全等. ( 可简写成“角角边”或“AAS”)
也就是说、三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
BC = B'C'
∴ △ABC ≌ △A'B'C' ( AAS )
A
C
B
A'
C'
B'
针对训练
1. 如图,AB⊥BC, AD⊥DC,垂足分别为 B,D,∠l =∠2.
求证:AB = AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC,
∴ ∠B =∠D = 90°.
在△ABC 和△ADC 中
∠B =∠D = 90°
∠1 =∠2
AC = AC
∴△ABC≌△ADC ( AAS ).
∴ AB = AD
A
B
C
D
1
2
2.如图,要测量池塘两岸相对的两点 A,B 的距离,可以在池塘外取 AB 的垂线 BF 上的两点 C、D,使 BC = CD,再画出 BF 的垂线 DE,使 E 与A,C 在一条直线上,这时测得 DE 的长度就是 AB 的长,为什么
A
B
C
D
F
E
证明:∵AB⊥BF,DE⊥BF,
∴∠B =∠CDE = 90°.
在△ABC 和△EDC 中
∠B =∠CDE = 90°
BC = CD
∠ACB =∠ECD ( 对顶角相等 )
∴△ABC≌△EDC (ASA)
∴AB = DE
A
B
C
D
F
E
随堂练习
1.已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED,AC∥EF. 求证:△ABC≌△EDF.
证明:∵ AB∥ED,AC∥EF,
∴ ∠B=∠D,∠ACB=∠EFD.
在△ABC与△EDF中,
∵
∴△ ABC ≌△ EDF. (AAS)
2.△ABC是等腰三角形,AD、BE 分别是∠CAB、∠CBA 的平分线,△ABD和△BAE 全等吗?试说明理由.
∴ ∠BAD =∠ABE
解:∵ △ABC是等腰三角形
∴ AC=BC ∠CAB=∠CBA
又∵ AD、BE 分别是∠CAB、∠CBA 的角平分线
∴ ∠BAD= ∠CAB
∠ABE= ∠CBA
∵
∠BAD =∠ABE
AB=AB
∠EAB=∠DBA
∴△ABD≌△BAE (ASA)
在△ABD和△BAE中,
注意
角边角
图形中的隐藏条件. ( 如:公共边、公共角、对顶角等 )
两角及其夹边分别相等的两个三角形全等( “角边角”或“ASA”).
两角分别相等且其中一组等角的对边相等的两个三角形全等(“角角边”或“AAS”).
角角边
课堂小结
用“ASA”或“AAS”
判定三角形全等
对应相等的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一 定
(SSS)
不一定
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十二章 全等三角形
第3课时 用“ASA”或“AAS”判定三角形全等
第2节 三角形全等的判定
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握基本事实:两角及其夹边分别相等的两个三角形全等.
2. 证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等.
学习目标
重点
重点
我们已经学习了哪些判定两个三角形全等的方法?
三个条件
④两角一边
③两边一角
②三边
①三角
不行
“边边边”或“SSS”
?
“边角边”或“SAS”
新课引入
思考
A
C
B
A'
C'
B'
A
C
B
A'
C'
B'
已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置上有几种可能性呢?
“两角及夹边”
“两角和其中一角的对边”
一 三角形全等的判定(“角边角”)
新知学习
先任意画出一个△ABC,再画出一个△A'B'C',使 A'B' = AB,
∠A' =∠A,∠B' =∠B(即两角和它们的夹边分别相等). 把画好的△A'B'C' 剪下来,放到△ABC 上,它们全等吗?
探究1
画法:(1) 画 A'B' = AB;
(2) 在 A'B' 的同旁画∠DA'B' =∠A,∠EB'A' =∠B,A'D, B'E 相交于点 C'.
A
B
C
A'
B'
C'
E'
D'
如图,已知△ABC. 画一个△A'B'C',使A'B' = AB,∠A' =∠A,∠B' =∠B .
现象:两个三角形能完全重合.
说明:这两个三角形全等.
两角和它们的夹边分别相等的两个三角形全等. ( 可简写成“角边角”或“ASA”)
由探究1可以得到以下基本事实,用它可以判定两个三角形全等:
归纳
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
A'B' = AB
∴ △ABC ≌ △A'B'C' ( ASA )
A
B
C
A'
B'
C'
例1 如图,点 D 在 AB 上,点 E 在 AC 上,BA = AC,∠B =∠C.
求证:AE = AD.
目标: AE = AD
△ABE≌△ACD
A
D
B
E
C
证明:在△ABE 和△ACD 中,
∠B =∠C
AB = AC
∠A =∠A ( 公共角 )
∵△ABE ≌△ACD ( ASA )
∴AE = AD
A
D
B
E
C
例2 如图,在△ABC 和△A'B'C' 中,∠A' =∠A,∠B' =∠B,B'C' = BC. 求证:△A'B'C' ≌△ABC .
A
C
B
A'
C'
B'
分析:如果能证明∠C' =∠C,就可以利用“角边角”证明△ABC和△A'B'C' 全等.由三角形内角和定理可以证明∠C' =∠C.
二 三角形全等的判定(“角角边”)
证明:在△ABC 中,∠A +∠B +∠C = 180°,
∴∠C =180°- ∠A -∠B.
同理,∠C' = 180°-∠A' -∠B'.
∵∠A =∠A',∠B =∠B', ∴∠C =∠C'.
在△ ABC 与△A'B'C' 中,
∠C =∠C'
∵ BC = B'C',
∠B =∠B',
∴△ABC≌△A'B'C' (ASA)
A
C
B
A'
C'
B'
因此,我们可以得到下面的结论:
两角和其中一角的对边分别相等的两个三角形全等. ( 可简写成“角角边”或“AAS”)
也就是说、三角形的两个角的大小和其中一个角的对边的长度确定了,这个三角形的形状、大小就确定了.
用符号语言表达:
在△ABC 与 △A'B'C' 中
∵
∠A' = ∠A
∠B' =∠B
BC = B'C'
∴ △ABC ≌ △A'B'C' ( AAS )
A
C
B
A'
C'
B'
针对训练
1. 如图,AB⊥BC, AD⊥DC,垂足分别为 B,D,∠l =∠2.
求证:AB = AD.
A
B
C
D
1
2
证明:∵AB⊥BC,AD⊥DC,
∴ ∠B =∠D = 90°.
在△ABC 和△ADC 中
∠B =∠D = 90°
∠1 =∠2
AC = AC
∴△ABC≌△ADC ( AAS ).
∴ AB = AD
A
B
C
D
1
2
2.如图,要测量池塘两岸相对的两点 A,B 的距离,可以在池塘外取 AB 的垂线 BF 上的两点 C、D,使 BC = CD,再画出 BF 的垂线 DE,使 E 与A,C 在一条直线上,这时测得 DE 的长度就是 AB 的长,为什么
A
B
C
D
F
E
证明:∵AB⊥BF,DE⊥BF,
∴∠B =∠CDE = 90°.
在△ABC 和△EDC 中
∠B =∠CDE = 90°
BC = CD
∠ACB =∠ECD ( 对顶角相等 )
∴△ABC≌△EDC (ASA)
∴AB = DE
A
B
C
D
F
E
随堂练习
1.已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED,AC∥EF. 求证:△ABC≌△EDF.
证明:∵ AB∥ED,AC∥EF,
∴ ∠B=∠D,∠ACB=∠EFD.
在△ABC与△EDF中,
∵
∴△ ABC ≌△ EDF. (AAS)
2.△ABC是等腰三角形,AD、BE 分别是∠CAB、∠CBA 的平分线,△ABD和△BAE 全等吗?试说明理由.
∴ ∠BAD =∠ABE
解:∵ △ABC是等腰三角形
∴ AC=BC ∠CAB=∠CBA
又∵ AD、BE 分别是∠CAB、∠CBA 的角平分线
∴ ∠BAD= ∠CAB
∠ABE= ∠CBA
∵
∠BAD =∠ABE
AB=AB
∠EAB=∠DBA
∴△ABD≌△BAE (ASA)
在△ABD和△BAE中,
注意
角边角
图形中的隐藏条件. ( 如:公共边、公共角、对顶角等 )
两角及其夹边分别相等的两个三角形全等( “角边角”或“ASA”).
两角分别相等且其中一组等角的对边相等的两个三角形全等(“角角边”或“AAS”).
角角边
课堂小结
用“ASA”或“AAS”
判定三角形全等
对应相等的元素 两边一角 两角一边 三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一 定
(SSS)
不一定
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
