13.1.2 第1课时 线段垂直平分线的性质与判定 课件(共28张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 13.1.2 第1课时 线段垂直平分线的性质与判定 课件(共28张PPT)【2023秋人教八上数学高效实用备课】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 线段垂直平分线的性质与判定
第1节 轴对称
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 能用尺规作图:过一点作已知直线的垂线.
2. 探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上.
学习目标
重点
重点
线段的垂直平分线的定义是什么?
l
C
B
A
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线 .
符号语言:
点 C 是线段 AB 的中点,且 l⊥AB 于 C,直线 l 是线段 AB 的垂直平分线.
新课引入
如图,直线 l 垂直平分线段 AB ,P1,P2,P3,…是 l 上的点, 分别量一量点P1,P2,P3, ... 到点 A 与点 B 的距离,你有什么发现?
探究
P1A = P1B,P2A = P2B, P3A = P3B.
一 线段垂直平分线的性质
新知学习
可以发现,点P1,P2,P3, ... 到点A的距离与它们到点B的距离分别相等.如果把线段AB沿直线 l 对折,线段P1A与P1B、线段P2A与P2B、线段P3A与P3B……都是重合的,因此它们也分别相等.
由此我们可以得出线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
试着证明这个性质.
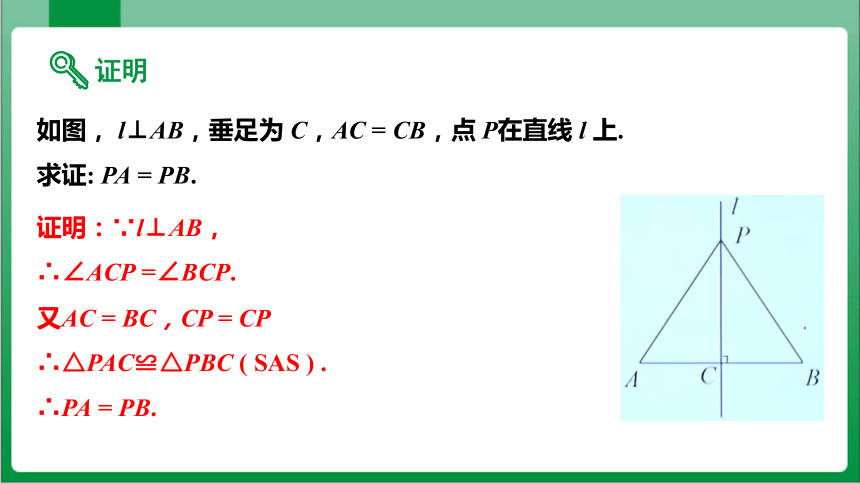
如图, l⊥AB,垂足为 C,AC = CB,点 P在直线 l 上.
求证: PA = PB.
证明
证明:∵l⊥AB,
∴∠ACP =∠BCP.
又AC = BC,CP = CP
∴△PAC≌△PBC ( SAS ) .
∴PA = PB.
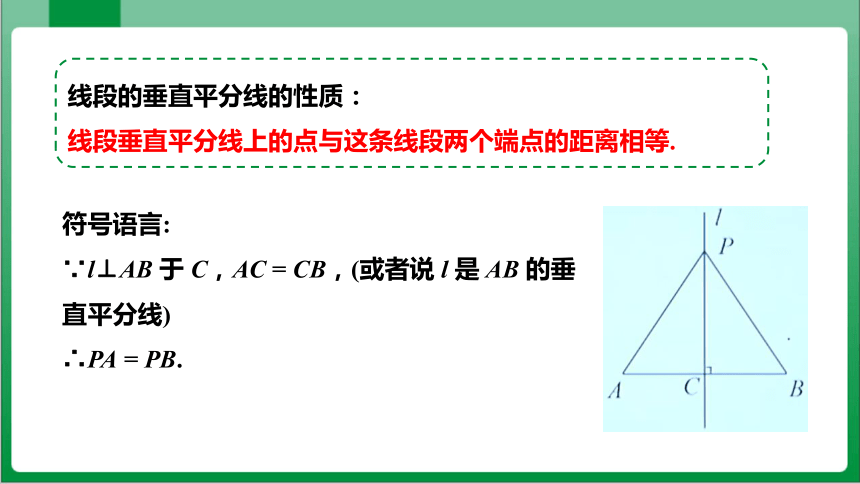
线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵l⊥AB 于 C,AC = CB,(或者说 l 是 AB 的垂直平分线)
∴PA = PB.
反过来,如果 PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
思考
A
B
P
二 线段垂直平分线的判定
分析:过点P作直线l,使得l⊥AB,垂足为O.
只要证明Rt△PAO≌Rt△PBO,就可求证.
如图,线段AB外任意一点P到点A,点B的距离相等.
求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为O.
∵l⊥AB, ∴∠POA=∠POB=90°.
在Rt△PAO和Rt△PBO中,
PA=PB,
PO=PO,
∴Rt△PAO≌Rt△PBO(HL).
∴AO=BO.
∵AO=BO,∠POA=∠POB=90°,
∴点P在线段AB的垂直平分线上.
A
B
P
l
O
归纳
通过证明可以得到:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
P
l
O
符号语言:
已知线段AB,∵PA=PB,
∴点P在线段AB的垂直平分线上.
从线段垂直平分线的性质和判定两个结论可以看出:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在 l 上,所以直线 l 可以看成与两点A,B的距离相等的所有点的集合.
A
B
P
l
O
例1 如图,AD⊥BC,BD = DC,点 C 在 AE 的垂直平分线上.
(1) AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
解:(1) ∵AD⊥BC,BD = DC,
∴AB = AC.
∵点 C 在 AE 的垂直平分线上,
∴AC = CE.
∴AB = AC = CE.
∴AB + BD = CE + DC = DE.
(2) 由 (1) 知 DE = AB + BD,
∵△ABC 的周长是 AB + BC+ AC = AB + BC+ CE = 13.
∴△ABE的周长为 AB + BC+ CE + AE
= 13+6= 19.
(2) 若 AE = 6,△ABC 的周长是 13,求△ABE 的周长.
例2 如图,四边形ABCD中,AB=AD,BC=DC,E是AC上一点,连接DE,BE,求证:∠ABE=∠ADE.
A
D
E
B
C
证明:连接DB.
∵AB=AD,BC=DC,
∴点A和点C都在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
∵E是AC上的一点, ∴BE=DE.
在△ABE和△ADE中,
AB=AD,
BE=DE,
AE=AE,
∴ △ABE≌△ADE(SSS). ∴∠ABE=∠ADE.
A
D
E
B
C
三 尺规作图:经过已知直线外一点作这条直线的垂线.
例3 已知:直线AB和AB外一点C(如图).
求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使点K和点C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
A
B
C
D
E
K
F
A
B
C
D
E
K
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
1. 如图,在△ABC 中,AB = AC,DE 是 AB 的垂直平分线,△BCE 的周长为 24,BC = 10,则 AB = _______ .
分析:由 DE 是 AB 的垂直平分线可知:AE = BE.
△BCE 的周长为 BE + CE + BC
= AE + CE + BC = AC + BC = 24.
而 BC = 10,
∴AB = AC = 14.
14
随堂练习
2.已知,如图,AM 是△ABC 的角平分线,MF 是线段 BC 的垂直平分线,MD⊥AB 于 D,ME⊥AE 于 E,求证: BD = CE.
分析:由 AM 是△ABC 的角平分线 MD⊥AB 于 D,ME⊥AE 于 E 可知,MD = ME.
连接 MB,MC,
由 MF 是线段 BC 的垂直平分线,
有 MB = MC.
进而可证 Rt△BDM≌Rt△CEM (HL)
证明:连接 MB,MC,
∵AM 是△ABC 的角平分线,MD⊥AB,ME⊥AE,
∴MD = ME .
∵MF 是线段 BC 的垂直平分线,
∴MB = MC.
在 Rt△BDM 和 Rt△CEM 中
MD = ME,
MB = MC,
∴Rt△BDM≌Rt△CEM ( HL )
∴BD = CE.
遇到线段的垂直平分线上的点时,通常会连接这个点和线段两个端点,得到相应的两条线段相等.
3. 如图所示,在△ABC 中,AD 平分∠BAC,DE⊥AB 于点 E,DF⊥AC 于点 F,试说明 AD 与 EF 的关系.
解:∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵ AD=AD,
∴△ADE≌△ADF(AAS).
∴ AE=AF,DE=DF.
∴ A、D 均在线段 EF 的垂直平分线上,
即直线 AD 垂直平分线段 EF.
A
B
C
D
E
F
4.如图,某乳业公司要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站M应建在什么地方,才能使A,B到它的距离相等
可以先作线段AB的垂直平分线,与街道的交点就是奶站M的位置.
居民区A
·
居民区B
·
街道
·
M
线段垂直平分线上的点与这条线段两个端点的距离相等.
线段垂直平分线
尺规作图
线段垂直平
分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平
分线的性质
经过已知直线外一点作这条直线的垂线.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 线段垂直平分线的性质与判定
第1节 轴对称
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 能用尺规作图:过一点作已知直线的垂线.
2. 探索并证明线段垂直平分线的性质定理:线段垂直平分线上的点与这条线段两个端点的距离相等;反之,到线段两端距离相等的点在线段的垂直平分线上.
学习目标
重点
重点
线段的垂直平分线的定义是什么?
l
C
B
A
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线 .
符号语言:
点 C 是线段 AB 的中点,且 l⊥AB 于 C,直线 l 是线段 AB 的垂直平分线.
新课引入
如图,直线 l 垂直平分线段 AB ,P1,P2,P3,…是 l 上的点, 分别量一量点P1,P2,P3, ... 到点 A 与点 B 的距离,你有什么发现?
探究
P1A = P1B,P2A = P2B, P3A = P3B.
一 线段垂直平分线的性质
新知学习
可以发现,点P1,P2,P3, ... 到点A的距离与它们到点B的距离分别相等.如果把线段AB沿直线 l 对折,线段P1A与P1B、线段P2A与P2B、线段P3A与P3B……都是重合的,因此它们也分别相等.
由此我们可以得出线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
试着证明这个性质.
如图, l⊥AB,垂足为 C,AC = CB,点 P在直线 l 上.
求证: PA = PB.
证明
证明:∵l⊥AB,
∴∠ACP =∠BCP.
又AC = BC,CP = CP
∴△PAC≌△PBC ( SAS ) .
∴PA = PB.
线段的垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵l⊥AB 于 C,AC = CB,(或者说 l 是 AB 的垂直平分线)
∴PA = PB.
反过来,如果 PA = PB,那么点 P 是否在线段 AB 的垂直平分线上呢?
思考
A
B
P
二 线段垂直平分线的判定
分析:过点P作直线l,使得l⊥AB,垂足为O.
只要证明Rt△PAO≌Rt△PBO,就可求证.
如图,线段AB外任意一点P到点A,点B的距离相等.
求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为O.
∵l⊥AB, ∴∠POA=∠POB=90°.
在Rt△PAO和Rt△PBO中,
PA=PB,
PO=PO,
∴Rt△PAO≌Rt△PBO(HL).
∴AO=BO.
∵AO=BO,∠POA=∠POB=90°,
∴点P在线段AB的垂直平分线上.
A
B
P
l
O
归纳
通过证明可以得到:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
A
B
P
l
O
符号语言:
已知线段AB,∵PA=PB,
∴点P在线段AB的垂直平分线上.
从线段垂直平分线的性质和判定两个结论可以看出:在线段AB的垂直平分线l上的点与A,B的距离都相等;反过来,与A,B的距离相等的点都在 l 上,所以直线 l 可以看成与两点A,B的距离相等的所有点的集合.
A
B
P
l
O
例1 如图,AD⊥BC,BD = DC,点 C 在 AE 的垂直平分线上.
(1) AB,AC,CE 的长度有什么关系?AB + BD 与 DE 有什么关系?
解:(1) ∵AD⊥BC,BD = DC,
∴AB = AC.
∵点 C 在 AE 的垂直平分线上,
∴AC = CE.
∴AB = AC = CE.
∴AB + BD = CE + DC = DE.
(2) 由 (1) 知 DE = AB + BD,
∵△ABC 的周长是 AB + BC+ AC = AB + BC+ CE = 13.
∴△ABE的周长为 AB + BC+ CE + AE
= 13+6= 19.
(2) 若 AE = 6,△ABC 的周长是 13,求△ABE 的周长.
例2 如图,四边形ABCD中,AB=AD,BC=DC,E是AC上一点,连接DE,BE,求证:∠ABE=∠ADE.
A
D
E
B
C
证明:连接DB.
∵AB=AD,BC=DC,
∴点A和点C都在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线.
∵E是AC上的一点, ∴BE=DE.
在△ABE和△ADE中,
AB=AD,
BE=DE,
AE=AE,
∴ △ABE≌△ADE(SSS). ∴∠ABE=∠ADE.
A
D
E
B
C
三 尺规作图:经过已知直线外一点作这条直线的垂线.
例3 已知:直线AB和AB外一点C(如图).
求作:AB的垂线,使它经过点C.
作法:(1)任意取一点K,使点K和点C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
A
B
C
D
E
K
F
A
B
C
D
E
K
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
直线CF就是所求作的垂线.
1. 如图,在△ABC 中,AB = AC,DE 是 AB 的垂直平分线,△BCE 的周长为 24,BC = 10,则 AB = _______ .
分析:由 DE 是 AB 的垂直平分线可知:AE = BE.
△BCE 的周长为 BE + CE + BC
= AE + CE + BC = AC + BC = 24.
而 BC = 10,
∴AB = AC = 14.
14
随堂练习
2.已知,如图,AM 是△ABC 的角平分线,MF 是线段 BC 的垂直平分线,MD⊥AB 于 D,ME⊥AE 于 E,求证: BD = CE.
分析:由 AM 是△ABC 的角平分线 MD⊥AB 于 D,ME⊥AE 于 E 可知,MD = ME.
连接 MB,MC,
由 MF 是线段 BC 的垂直平分线,
有 MB = MC.
进而可证 Rt△BDM≌Rt△CEM (HL)
证明:连接 MB,MC,
∵AM 是△ABC 的角平分线,MD⊥AB,ME⊥AE,
∴MD = ME .
∵MF 是线段 BC 的垂直平分线,
∴MB = MC.
在 Rt△BDM 和 Rt△CEM 中
MD = ME,
MB = MC,
∴Rt△BDM≌Rt△CEM ( HL )
∴BD = CE.
遇到线段的垂直平分线上的点时,通常会连接这个点和线段两个端点,得到相应的两条线段相等.
3. 如图所示,在△ABC 中,AD 平分∠BAC,DE⊥AB 于点 E,DF⊥AC 于点 F,试说明 AD 与 EF 的关系.
解:∵ AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵ AD=AD,
∴△ADE≌△ADF(AAS).
∴ AE=AF,DE=DF.
∴ A、D 均在线段 EF 的垂直平分线上,
即直线 AD 垂直平分线段 EF.
A
B
C
D
E
F
4.如图,某乳业公司要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站M应建在什么地方,才能使A,B到它的距离相等
可以先作线段AB的垂直平分线,与街道的交点就是奶站M的位置.
居民区A
·
居民区B
·
街道
·
M
线段垂直平分线上的点与这条线段两个端点的距离相等.
线段垂直平分线
尺规作图
线段垂直平
分线的判定
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平
分线的性质
经过已知直线外一点作这条直线的垂线.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
