13.3.1 等腰三角形第1课时等腰三角形的性质 课件(共26张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 13.3.1 等腰三角形第1课时等腰三角形的性质 课件(共26张PPT)【2023秋人教八上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 17:37:00 | ||
图片预览







文档简介
(共26张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 等腰三角形的性质
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 理解等腰三角形的概念.
2. 探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;等腰三角形顶角平分线、底边上的中线及底边上的高线重合.
学习目标
重点
难点
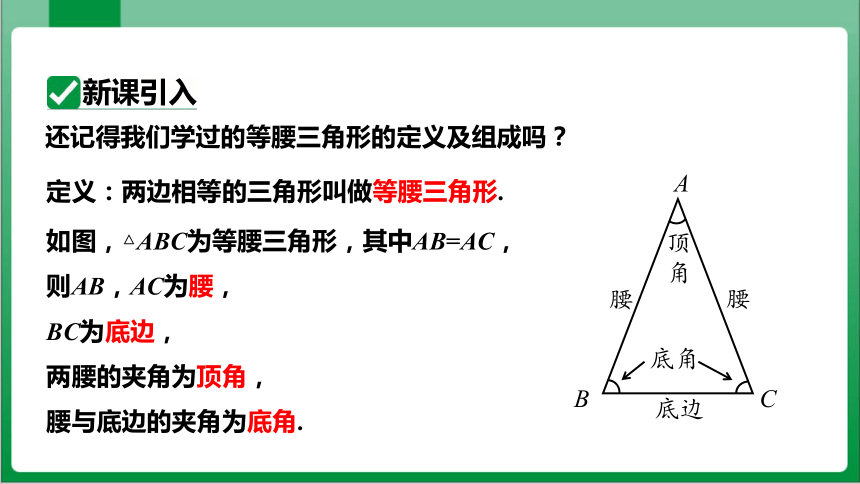
定义:两边相等的三角形叫做等腰三角形.
A
B
C
腰
腰
底边
顶
角
底角
还记得我们学过的等腰三角形的定义及组成吗?
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,
BC为底边,
两腰的夹角为顶角,
腰与底边的夹角为底角.
新课引入
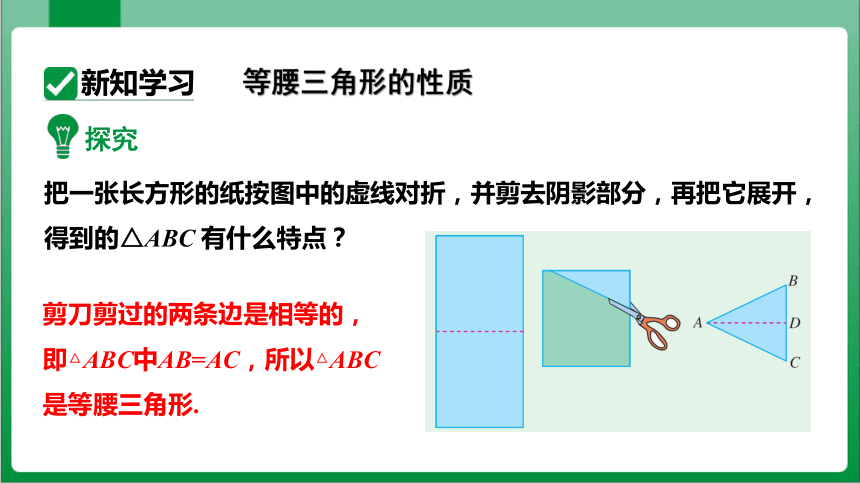
探究
把一张长方形的纸按图中的虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
等腰三角形的性质
剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.
新知学习
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
由这些重合的线段和角,你能发现等腰三角形的性质吗?说出你的猜想.
AB 与 AC
BD 与 CD
AD 与 AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜想 1:等腰三角形的两个底角相等.
猜想 2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
试着证明这2个猜想.
已知:△ABC 中,AB = AC,求证:∠B =∠C.
证明
A
B
C
证明:作底边BC的中线 AD,
AB = AC,
BD = CD,
AD = AD,
∴△BAD≌△CAD (SSS)
∴∠B =∠C.
D
方法一:作底边上的中线
方法二:作顶角的平分线
证明:作顶角∠BAC的平分线 AD,
AB = AC
∠BAD =∠CAD
AD = AD
∴△BAD ≌△CAD (SAS)
∴∠B =∠C.
A
B
C
D
方法三:作底边上的高线
证明:作 BC 边上的高线 AD.
在 Rt△BAD 和 Rt△CAD 中
AB = AC
AD = AD
∴△BAD≌△CAD (HL)
∴∠B =∠C .
A
B
C
D
性质 1:等腰三角形的两个底角相等 ( 简写成:等边对等角 ) .
归纳
符号语言:
如图,在△ABC中,
∵AB = AC
∴∠B =∠C (等边对等角)
A
B
C
性质 2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 ( 简写成:三线合一 ).
A
B
C
D
符号语言 1:
如图,在△ABC中,
∵AB = AC,AD⊥BC
∴BD = CD,∠BAD =∠CAD ( 三线合一 )
符号语言 3:
如图,在△ABC中,
∵AB = AC,∠BAD=∠CAD
∴AD⊥BC,BD = CD ( 三线合一 )
符号语言2:
如图,在△ABC中,
∵AB = AC,BD = CD,
∴AD⊥BC,∠BAD = ∠CAD( 三线合一 )
A
B
C
D
从以上证明也可以得出,等腰三角形底边上的中线的左右两部分经翻折可以重合,等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴
A
B
C
D
例1 如图,在△ABC 中 ,AB = AC,点 D 在 AC 上,且 BD = BC = AD,求△ABC 各角的度数.
解:∵AB = AC,BD = BC = AD,
∴∠ABC =∠C =∠BDC,
∠A =∠ABD(等边对等角).
设∠A = x,
则∠BDC =∠A +∠ABD = 2x,
从而∠ABC =∠C =∠BDC = 2x,
于是在△ABC 中,有
∠A +∠ABC +∠C = x + 2x + 2x = 180°
解得 x = 36°,
在△ABC 中,
∠A = 36°,∠ABC =∠C = 72°.
针对训练
1. (1) 等腰三角形一个底角为75°,它的另外两个角为__________;
(2) 等腰三角形一个角为36°,它的另外两个角为____________________;
(3) 等腰三角形一个角为120°,它的另外两个角为__________.
75°,30°
72°,72° 或 36° ,108°
30°,30°
1. 在△ABC 中,AB = AC,AB 的垂直平分线与 AC 所在的直线相交得的锐角为 50°,则底角的大小为 .
A
B
C
A
B
C
70° 或 20°
分析:当题目未给定三角形的形状时,一般需考虑锐角三角形、钝角三角形、直角三角形三种情况.
随堂练习
2.已知等腰三角形一边长为4,周长为10,则另两边长分别为( )
A.4,2 B.3,3
C.4,2或3,3 D.以上都不对
C
未指明边是腰或底,需分类讨论.
3.如图,△ABC 中,AB = AC,AD 和 BE 是高,它们相交于点 H,且AE = BE,求证:AH = 2BD.
分析:
运用等腰三角形“三线合一”,得
2BD = BC,只需证明△AHE≌△BCE .
证明:∵AB = AC,AD 是高,BE 是高,
∴BC = 2BD.
∠ADC = 90°,∠AEH =∠BEC = 90°
∴∠HAE +∠C = 90°,∠CBE +∠C = 90°
∴∠HAE =∠CBE .
在△AHE 和△BCE 中,
∠HAE =∠CBE,
AE = BE,
∠AEH =∠BEC,
∴△AHE≌△BCE(ASA).
∴AH = BC.
又∵BC = 2BD,
∴AH = 2BD.
等腰三角形的两个底角相等 ( 简写成:等边对等角 ) .
等腰三角形
的性质
性质1
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 ( 简写成:三线合一 ).
性质2
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 等腰三角形的性质
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 理解等腰三角形的概念.
2. 探索并证明等腰三角形的性质定理:等腰三角形的两个底角相等;等腰三角形顶角平分线、底边上的中线及底边上的高线重合.
学习目标
重点
难点
定义:两边相等的三角形叫做等腰三角形.
A
B
C
腰
腰
底边
顶
角
底角
还记得我们学过的等腰三角形的定义及组成吗?
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,
BC为底边,
两腰的夹角为顶角,
腰与底边的夹角为底角.
新课引入
探究
把一张长方形的纸按图中的虚线对折,并剪去阴影部分,再把它展开,得到的△ABC 有什么特点?
等腰三角形的性质
剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.
新知学习
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段 重合的角
由这些重合的线段和角,你能发现等腰三角形的性质吗?说出你的猜想.
AB 与 AC
BD 与 CD
AD 与 AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜想 1:等腰三角形的两个底角相等.
猜想 2:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合.
试着证明这2个猜想.
已知:△ABC 中,AB = AC,求证:∠B =∠C.
证明
A
B
C
证明:作底边BC的中线 AD,
AB = AC,
BD = CD,
AD = AD,
∴△BAD≌△CAD (SSS)
∴∠B =∠C.
D
方法一:作底边上的中线
方法二:作顶角的平分线
证明:作顶角∠BAC的平分线 AD,
AB = AC
∠BAD =∠CAD
AD = AD
∴△BAD ≌△CAD (SAS)
∴∠B =∠C.
A
B
C
D
方法三:作底边上的高线
证明:作 BC 边上的高线 AD.
在 Rt△BAD 和 Rt△CAD 中
AB = AC
AD = AD
∴△BAD≌△CAD (HL)
∴∠B =∠C .
A
B
C
D
性质 1:等腰三角形的两个底角相等 ( 简写成:等边对等角 ) .
归纳
符号语言:
如图,在△ABC中,
∵AB = AC
∴∠B =∠C (等边对等角)
A
B
C
性质 2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 ( 简写成:三线合一 ).
A
B
C
D
符号语言 1:
如图,在△ABC中,
∵AB = AC,AD⊥BC
∴BD = CD,∠BAD =∠CAD ( 三线合一 )
符号语言 3:
如图,在△ABC中,
∵AB = AC,∠BAD=∠CAD
∴AD⊥BC,BD = CD ( 三线合一 )
符号语言2:
如图,在△ABC中,
∵AB = AC,BD = CD,
∴AD⊥BC,∠BAD = ∠CAD( 三线合一 )
A
B
C
D
从以上证明也可以得出,等腰三角形底边上的中线的左右两部分经翻折可以重合,等腰三角形是轴对称图形,底边上的中线(顶角平分线、底边上的高)所在直线就是它的对称轴
A
B
C
D
例1 如图,在△ABC 中 ,AB = AC,点 D 在 AC 上,且 BD = BC = AD,求△ABC 各角的度数.
解:∵AB = AC,BD = BC = AD,
∴∠ABC =∠C =∠BDC,
∠A =∠ABD(等边对等角).
设∠A = x,
则∠BDC =∠A +∠ABD = 2x,
从而∠ABC =∠C =∠BDC = 2x,
于是在△ABC 中,有
∠A +∠ABC +∠C = x + 2x + 2x = 180°
解得 x = 36°,
在△ABC 中,
∠A = 36°,∠ABC =∠C = 72°.
针对训练
1. (1) 等腰三角形一个底角为75°,它的另外两个角为__________;
(2) 等腰三角形一个角为36°,它的另外两个角为____________________;
(3) 等腰三角形一个角为120°,它的另外两个角为__________.
75°,30°
72°,72° 或 36° ,108°
30°,30°
1. 在△ABC 中,AB = AC,AB 的垂直平分线与 AC 所在的直线相交得的锐角为 50°,则底角的大小为 .
A
B
C
A
B
C
70° 或 20°
分析:当题目未给定三角形的形状时,一般需考虑锐角三角形、钝角三角形、直角三角形三种情况.
随堂练习
2.已知等腰三角形一边长为4,周长为10,则另两边长分别为( )
A.4,2 B.3,3
C.4,2或3,3 D.以上都不对
C
未指明边是腰或底,需分类讨论.
3.如图,△ABC 中,AB = AC,AD 和 BE 是高,它们相交于点 H,且AE = BE,求证:AH = 2BD.
分析:
运用等腰三角形“三线合一”,得
2BD = BC,只需证明△AHE≌△BCE .
证明:∵AB = AC,AD 是高,BE 是高,
∴BC = 2BD.
∠ADC = 90°,∠AEH =∠BEC = 90°
∴∠HAE +∠C = 90°,∠CBE +∠C = 90°
∴∠HAE =∠CBE .
在△AHE 和△BCE 中,
∠HAE =∠CBE,
AE = BE,
∠AEH =∠BEC,
∴△AHE≌△BCE(ASA).
∴AH = BC.
又∵BC = 2BD,
∴AH = 2BD.
等腰三角形的两个底角相等 ( 简写成:等边对等角 ) .
等腰三角形
的性质
性质1
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合 ( 简写成:三线合一 ).
性质2
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
