13.3.2 等边三角形第1课时等边三角形的性质与判定 课件(共30张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 13.3.2 等边三角形第1课时等边三角形的性质与判定 课件(共30张PPT)【2023秋人教八上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 17:35:37 | ||
图片预览





文档简介
(共30张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 等边三角形的
性质与判定
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索等边三角形的性质定理:等边三角形的各角都等于60°.
2. 探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形.
学习目标
重点
重点
三角形按边分类
三角形
三边都不相等的三角形
等腰三角形
底与腰不等的等腰三角形
底与腰相等的等腰三角形(等边三角形)
等边三角形是三边都相等的特殊的等腰三角形.
新课引入
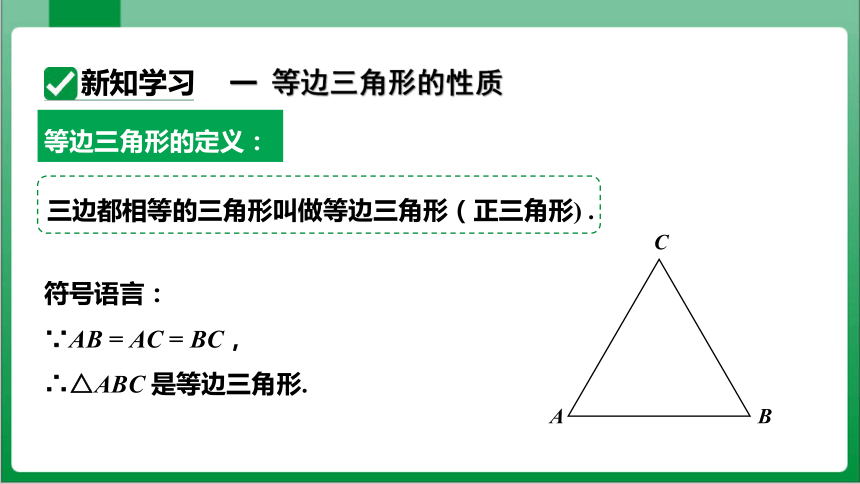
等边三角形的定义:
三边都相等的三角形叫做等边三角形(正三角形) .
C
A
B
符号语言:
∵AB = AC = BC,
∴△ABC 是等边三角形.
一 等边三角形的性质
新知学习
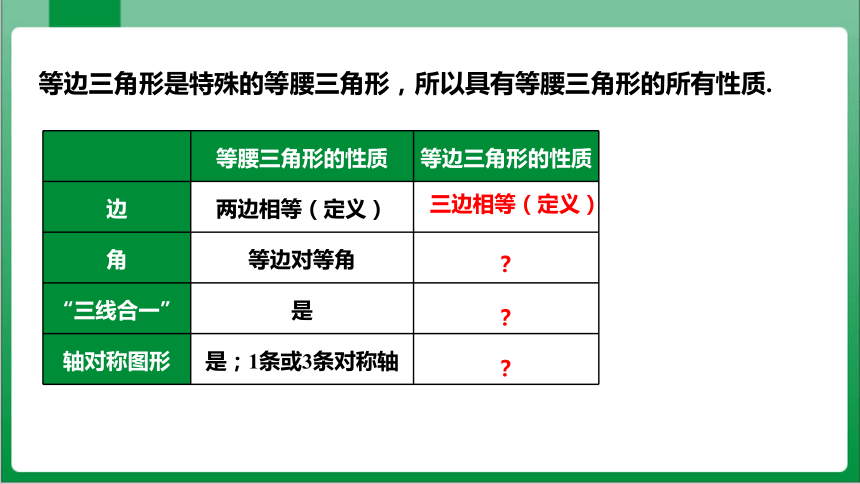
等边三角形是特殊的等腰三角形,所以具有等腰三角形的所有性质.
等腰三角形的性质 等边三角形的性质
边 两边相等(定义)
角 等边对等角
“三线合一” 是
轴对称图形 是;1条或3条对称轴
三边相等(定义)
?
?
?
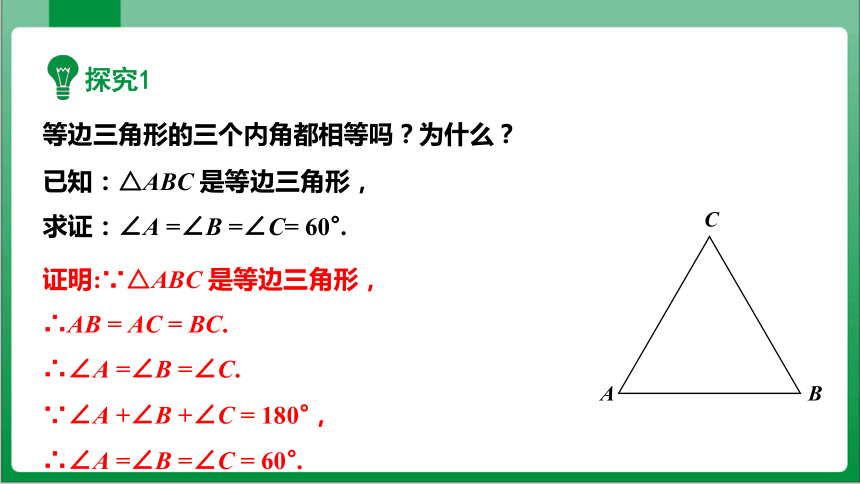
探究1
等边三角形的三个内角都相等吗?为什么?
C
A
B
已知:△ABC 是等边三角形,
求证:∠A =∠B =∠C= 60°.
证明:∵△ABC 是等边三角形,
∴AB = AC = BC.
∴∠A =∠B =∠C.
∵∠A +∠B +∠C = 180°,
∴∠A =∠B =∠C = 60°.
C
A
B
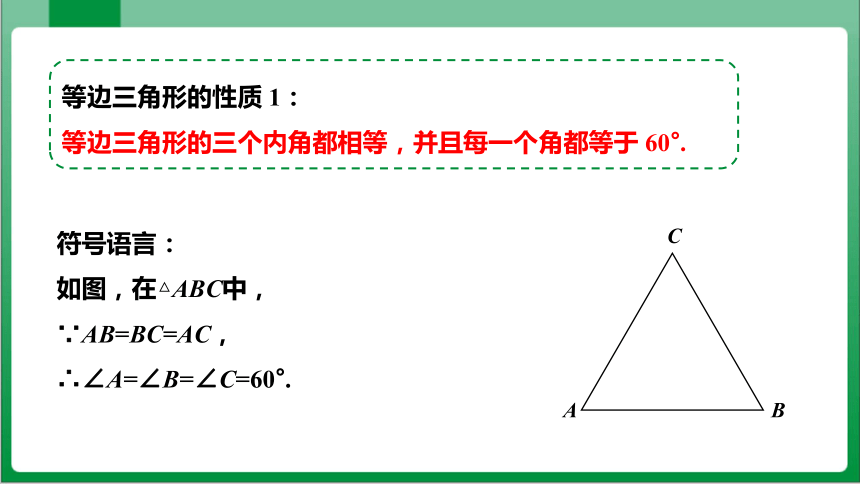
等边三角形的性质 1:
等边三角形的三个内角都相等,并且每一个角都等于 60°.
符号语言:
如图,在△ABC中,
∵AB=BC=AC,
∴∠A=∠B=∠C=60°.
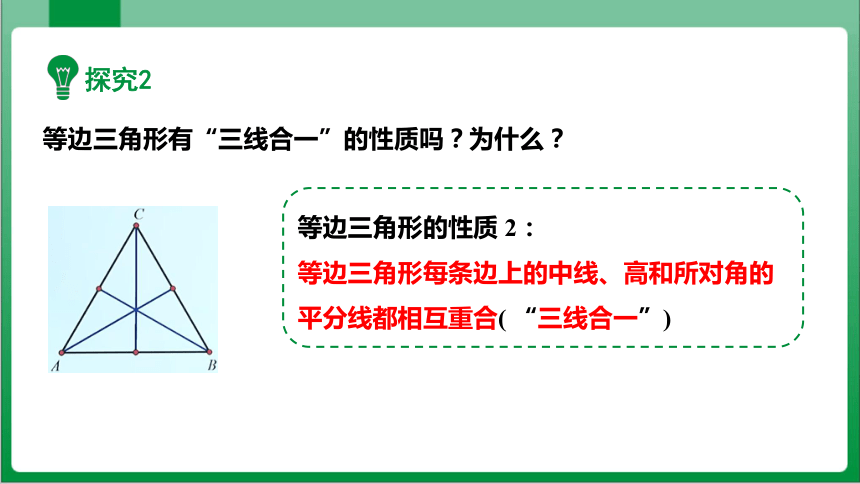
等边三角形有“三线合一”的性质吗?为什么?
等边三角形的性质 2:
等边三角形每条边上的中线、高和所对角的平分线都相互重合( “三线合一”)
探究2
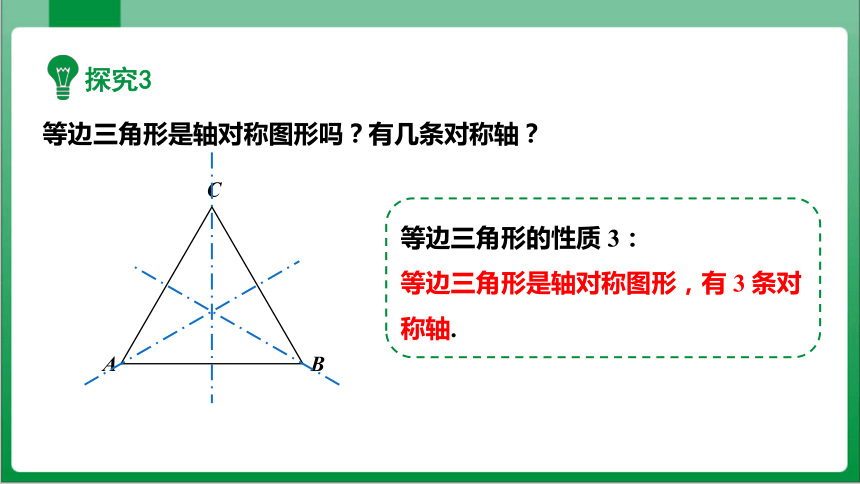
等边三角形是轴对称图形吗?有几条对称轴?
C
A
B
等边三角形的性质 3:
等边三角形是轴对称图形,有 3 条对称轴.
探究3
归纳
等腰三角形 等边三角形
边 两边相等(定义)
角 等边对等角
“三线合一” 是
轴对称图形 是;1条或3条对称轴
三边相等(定义)
三个内角都相等,都为60°
是
是;3条对称轴
例1 如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
A
B
C
D
E
解:∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,
∴∠DBE= ∠ABC=30°.
∵DE=DB, ∴∠E=∠DBE=30°.
∴∠CDE=∠ACB-∠E=60°-30°=30°.
∴CD=CE= AC= .
思考1
二 等边三角形的判定方法
一个三角形满足什么条件是等边三角形?
一般三角形
等边三角形
满足什么条件的三角形是等腰三角形?
方法一:从边看
有两边相等的三角形是等腰三角形(定义).
方法二:从角看
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
方法一:
三边都相等的三角形是等边三角形(定义).
方法二:
三个角都相等的三角形是等边三角形.
已知:在△ABC 中,∠A =∠B =∠C.
求证:△ABC 是等边三角形.
证明:
∵∠A =∠B,∠B =∠C,
∴BC = AC,AC = AB (等角对等边).
∴AB = BC = AC.
∴△ABC 是等边三角形.
C
A
B
证明
三个角都相等的三角形是等边三角形.
一个等腰三角形满足什么条件是等边三角形
分类讨论:
(1) 腰和底边相等的等腰三角形是等边三角形;
(2) 有一个角是60°的等腰三角形是等边三角形 .
等边三角形
思考2
等腰三角形
三边相等(定义)
证明
有一个角是60°的等腰三角形是等边三角形 .
如图:已知在△ABC中,AB=AC,∠A=60°.
证明:△ABC是等边三角形.
证明:∵AB=AC, ∴∠C=∠B .
∵∠A=60°,
∴∠B+∠C=180°-∠A=120° .
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
证明:∵AB=AC,∠B=60°,
∴∠C=∠B=60° .
∴∠A=180°-(∠B+∠C)=60°,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
A
B
C
如图:已知在△ABC中,AB=AC,∠B=60°.
证明:△ABC是等边三角形.
归纳
等边三角形的判定方法
名称 图形 判定方法
等边三角形
C
A
B
三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形
有一个角是 60° 的等腰三角形
是等边三角形
例2 如图,△ABC 是等边三角形,DE // BC,分别交 AB,AC 于点 D,E. 求证:△ADE 是等边三角形.
分析:
△ABC 是等边三角形
∠A = 60°
60°
△ADE 是等边三角形
思路1:三个角都相等.
思路 2:有一个角是 60° 的等腰三角形.
思路 3:三条边都相等.
思路 1:三个角都相等.
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED .
∴∠A =∠ADE =∠AED .
∴△ADE 是等边三角形.
思路 2:有一个角是 60° 的等腰三角形.
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C=60°
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠ADE =∠AED . ∴AD = AE.
∴△ADE 是等腰三角形.
∵∠A = 60°,∴△ADE 是等边三角形 .
思路 3:三条边都相等.
证明:∵△ ABC 是等边三角形,
∴∠A =∠B =∠C.
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠A=∠ADE,∠ADE =∠AED .
∴DE = AE,AD = AE.
即 AD = AE = DE.
∴△ADE 是等边三角形 .
1. 如图,等边三角形 ABC 的三条角平分线交于点 O,过点 O 作 DE∥BC,则这个图形中的等腰三角形共有 ( )
A. 4 个 B. 5 个
C. 6 个 D. 7 个
D
A
C
B
D
E
O
随堂练习
2.如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
解:∵△ABC是等边三角形,
∴∠ACB=∠A=60°,且AC=BC.
AC=CB,
∠A=∠BCE,
AD=CE,
∴△ADC≌△CEB(SAS), ∴∠CBE=∠ACD.
∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°.
E
D
B
C
A
证明:∵∠A=60°,OA=OB,
∴△AOB是等边三角形,
∴∠B=∠A=60°.
∵AB//CD, ∴∠C=∠A=60°,∠D=∠B=60°.
∴∠COD=60°, ∴∠C=∠D=∠COD=60°,
∴△OCD是等边三角形.
3.如图,AC和BD相交于点O,若OA=OB,∠A=60 ,且AB//CD.
求证:△OCD是等边三角形.
A
B
C
D
O
等边
三角形
定义
底=腰
特殊性
特殊性
边
三边相等
角
三个角都等于60°
轴对称性
轴对称图形,
每条边上都具有
“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
性质
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第1课时 等边三角形的
性质与判定
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索等边三角形的性质定理:等边三角形的各角都等于60°.
2. 探索等边三角形的判定定理:三个角都相等的三角形(或有一个角是60°的等腰三角形)是等边三角形.
学习目标
重点
重点
三角形按边分类
三角形
三边都不相等的三角形
等腰三角形
底与腰不等的等腰三角形
底与腰相等的等腰三角形(等边三角形)
等边三角形是三边都相等的特殊的等腰三角形.
新课引入
等边三角形的定义:
三边都相等的三角形叫做等边三角形(正三角形) .
C
A
B
符号语言:
∵AB = AC = BC,
∴△ABC 是等边三角形.
一 等边三角形的性质
新知学习
等边三角形是特殊的等腰三角形,所以具有等腰三角形的所有性质.
等腰三角形的性质 等边三角形的性质
边 两边相等(定义)
角 等边对等角
“三线合一” 是
轴对称图形 是;1条或3条对称轴
三边相等(定义)
?
?
?
探究1
等边三角形的三个内角都相等吗?为什么?
C
A
B
已知:△ABC 是等边三角形,
求证:∠A =∠B =∠C= 60°.
证明:∵△ABC 是等边三角形,
∴AB = AC = BC.
∴∠A =∠B =∠C.
∵∠A +∠B +∠C = 180°,
∴∠A =∠B =∠C = 60°.
C
A
B
等边三角形的性质 1:
等边三角形的三个内角都相等,并且每一个角都等于 60°.
符号语言:
如图,在△ABC中,
∵AB=BC=AC,
∴∠A=∠B=∠C=60°.
等边三角形有“三线合一”的性质吗?为什么?
等边三角形的性质 2:
等边三角形每条边上的中线、高和所对角的平分线都相互重合( “三线合一”)
探究2
等边三角形是轴对称图形吗?有几条对称轴?
C
A
B
等边三角形的性质 3:
等边三角形是轴对称图形,有 3 条对称轴.
探究3
归纳
等腰三角形 等边三角形
边 两边相等(定义)
角 等边对等角
“三线合一” 是
轴对称图形 是;1条或3条对称轴
三边相等(定义)
三个内角都相等,都为60°
是
是;3条对称轴
例1 如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
A
B
C
D
E
解:∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,
∴∠DBE= ∠ABC=30°.
∵DE=DB, ∴∠E=∠DBE=30°.
∴∠CDE=∠ACB-∠E=60°-30°=30°.
∴CD=CE= AC= .
思考1
二 等边三角形的判定方法
一个三角形满足什么条件是等边三角形?
一般三角形
等边三角形
满足什么条件的三角形是等腰三角形?
方法一:从边看
有两边相等的三角形是等腰三角形(定义).
方法二:从角看
有两个角相等的三角形是等腰三角形.
满足什么条件的三角形是等边三角形?
方法一:
三边都相等的三角形是等边三角形(定义).
方法二:
三个角都相等的三角形是等边三角形.
已知:在△ABC 中,∠A =∠B =∠C.
求证:△ABC 是等边三角形.
证明:
∵∠A =∠B,∠B =∠C,
∴BC = AC,AC = AB (等角对等边).
∴AB = BC = AC.
∴△ABC 是等边三角形.
C
A
B
证明
三个角都相等的三角形是等边三角形.
一个等腰三角形满足什么条件是等边三角形
分类讨论:
(1) 腰和底边相等的等腰三角形是等边三角形;
(2) 有一个角是60°的等腰三角形是等边三角形 .
等边三角形
思考2
等腰三角形
三边相等(定义)
证明
有一个角是60°的等腰三角形是等边三角形 .
如图:已知在△ABC中,AB=AC,∠A=60°.
证明:△ABC是等边三角形.
证明:∵AB=AC, ∴∠C=∠B .
∵∠A=60°,
∴∠B+∠C=180°-∠A=120° .
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
证明:∵AB=AC,∠B=60°,
∴∠C=∠B=60° .
∴∠A=180°-(∠B+∠C)=60°,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
A
B
C
如图:已知在△ABC中,AB=AC,∠B=60°.
证明:△ABC是等边三角形.
归纳
等边三角形的判定方法
名称 图形 判定方法
等边三角形
C
A
B
三条边都相等的三角形是等边三角形
三个角都相等的三角形是等边三角形
有一个角是 60° 的等腰三角形
是等边三角形
例2 如图,△ABC 是等边三角形,DE // BC,分别交 AB,AC 于点 D,E. 求证:△ADE 是等边三角形.
分析:
△ABC 是等边三角形
∠A = 60°
60°
△ADE 是等边三角形
思路1:三个角都相等.
思路 2:有一个角是 60° 的等腰三角形.
思路 3:三条边都相等.
思路 1:三个角都相等.
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C.
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED .
∴∠A =∠ADE =∠AED .
∴△ADE 是等边三角形.
思路 2:有一个角是 60° 的等腰三角形.
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C=60°
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠ADE =∠AED . ∴AD = AE.
∴△ADE 是等腰三角形.
∵∠A = 60°,∴△ADE 是等边三角形 .
思路 3:三条边都相等.
证明:∵△ ABC 是等边三角形,
∴∠A =∠B =∠C.
∵DE//BC,
∴∠B =∠ADE,∠C =∠AED.
∴∠A=∠ADE,∠ADE =∠AED .
∴DE = AE,AD = AE.
即 AD = AE = DE.
∴△ADE 是等边三角形 .
1. 如图,等边三角形 ABC 的三条角平分线交于点 O,过点 O 作 DE∥BC,则这个图形中的等腰三角形共有 ( )
A. 4 个 B. 5 个
C. 6 个 D. 7 个
D
A
C
B
D
E
O
随堂练习
2.如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
解:∵△ABC是等边三角形,
∴∠ACB=∠A=60°,且AC=BC.
AC=CB,
∠A=∠BCE,
AD=CE,
∴△ADC≌△CEB(SAS), ∴∠CBE=∠ACD.
∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°.
E
D
B
C
A
证明:∵∠A=60°,OA=OB,
∴△AOB是等边三角形,
∴∠B=∠A=60°.
∵AB//CD, ∴∠C=∠A=60°,∠D=∠B=60°.
∴∠COD=60°, ∴∠C=∠D=∠COD=60°,
∴△OCD是等边三角形.
3.如图,AC和BD相交于点O,若OA=OB,∠A=60 ,且AB//CD.
求证:△OCD是等边三角形.
A
B
C
D
O
等边
三角形
定义
底=腰
特殊性
特殊性
边
三边相等
角
三个角都等于60°
轴对称性
轴对称图形,
每条边上都具有
“三线合一”性质
判定
特殊性
三边法
三角法
等腰三角形法
性质
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
