13.3.2 等边三角形第2课时含30°角的直角三角形的性质 课件(共23张PPT)【2023秋人教八上数学高效实用备课】
文档属性
| 名称 | 13.3.2 等边三角形第2课时含30°角的直角三角形的性质 课件(共23张PPT)【2023秋人教八上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 17:34:10 | ||
图片预览






文档简介
(共23张PPT)
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第2课时 含 30°角的
直角三角形的性质
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索并证明含30° 角的直角三角形的性质:在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
2.会应用含30° 角的直角三角形的性质进行有关的证明和计算.
学习目标
重点
难点
回顾等边三角形的性质和判定.
等边三角形
性质 1. 三条边相等
2. 三个内角都相等,都为60°
3. “三线合一”
4. 轴对称图形 ( 3条对称轴 )
判定 1. 定义 ( 三条边相等 )
2. 三个角相等
3. 有一个角是 60° 的等腰三角形
新课引入
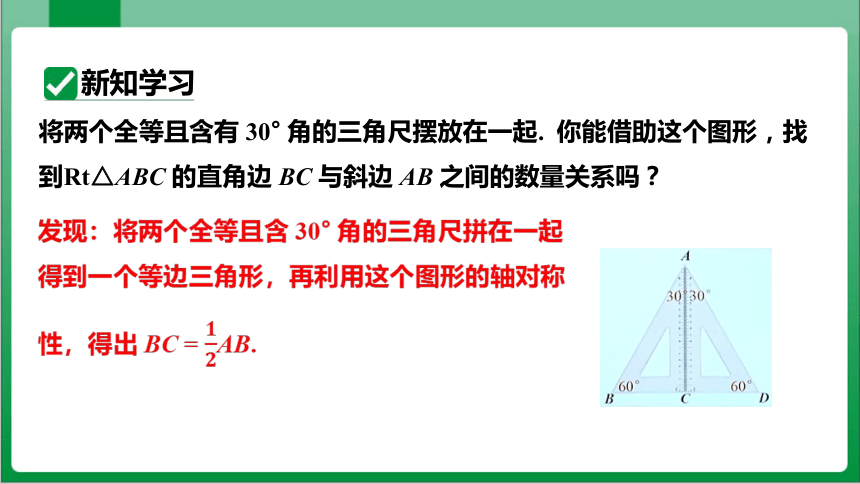
将两个全等且含有 30° 角的三角尺摆放在一起. 你能借助这个图形,找到Rt△ABC 的直角边 BC 与斜边 AB 之间的数量关系吗?
发现:将两个全等且含 30° 角的三角尺拼在一起得到一个等边三角形,再利用这个图形的轴对称性,得出 BC = AB.
新知学习
证明:∵△ADC 是△ABC 的轴对称图形
∴AB = AD,∠BAD = 2 × 30° = 60°.
∴△ABD 是等边三角形.
∵AC⊥BD.
你还能用其他方法证明吗?
∴BC = CD = AB.
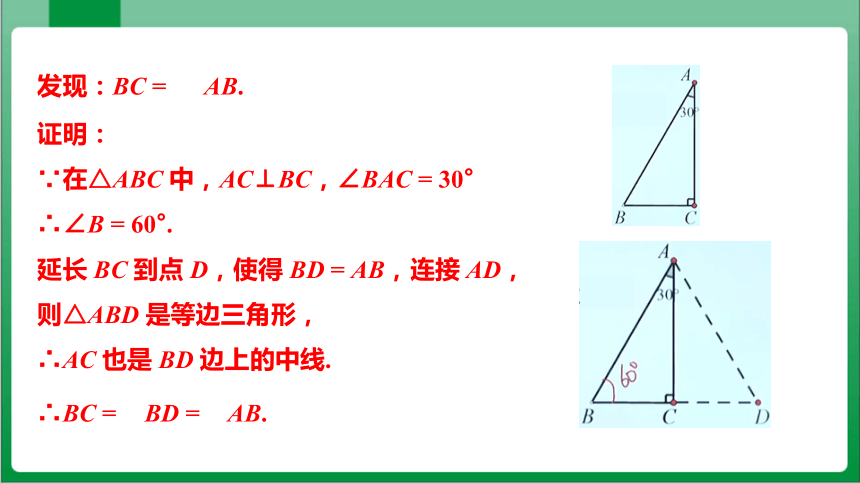
发现:BC = AB.
证明:
∵在△ABC 中,AC⊥BC,∠BAC = 30°
∴∠B = 60°.
延长 BC 到点 D,使得 BD = AB,连接 AD,
则△ABD 是等边三角形,
∴AC 也是 BD 边上的中线.
发现:BC = AB.
∴BC = BD = AB.
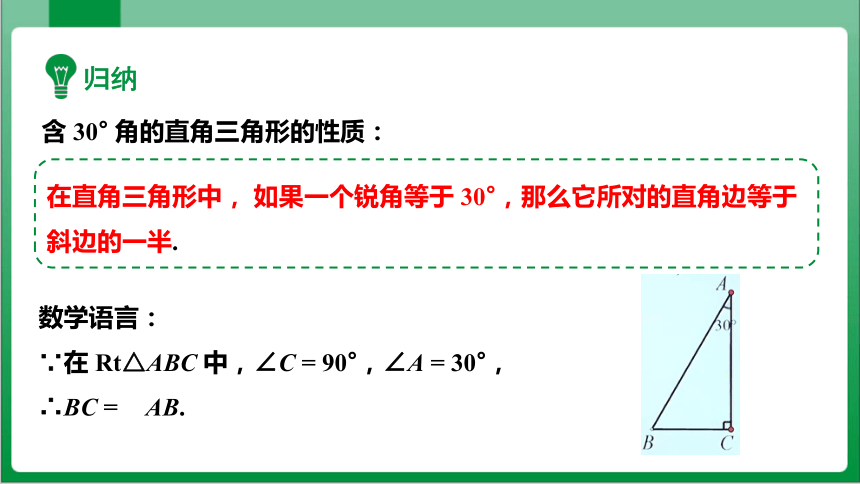
含 30° 角的直角三角形的性质:
归纳
在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
数学语言:
∵在 Rt△ABC 中,∠C = 90°,∠A = 30°,
∴BC = AB.
例1 下图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4m,∠A = 30°,立柱 BC,DE 要多长
解:∵DE⊥AC,BC⊥AC,∠A = 30°,
∴BC = AB,DE = AD.
∴BC = ×7.4 = 3.7(m) .
又 AD = AB,
∴DE = ×AD = ×3.7 = l.85(m).
答:立柱 BC 的长是 3.7 m,DE 的长是1.85 m.
1.三角形三个角的度数之 比为 1:2:3,它的最大边长等于 16 cm,则最小边长是 _______cm .
分析:设三角形三个角的度数分别为 k,2k,3k.
根据三角形内角和定理得,k + 2k + 3k = 180°,
解得 k = 30°, ∴3k = 90°.
由含 30° 角的直角三角形的性质,
8
∴最小边长等于 ×16 = 8 cm.
针对训练
分析:连接 AD,
∵AB = AC,D 是 BC 的中点,∴AD⊥BC.
∵∠BAC = 120°,∴∠B =∠C = 30°.
∵DE⊥AC,∴∠ADE = 30°.
在Rt△ADE 中,AD = 2AE,
在Rt△ABD 中,AB = 2AD = 4AE,
∴AB : AE = 4 : 1.
2.如图,在△ABC 中,AB = AC,∠BAC = 120°,D 是 BC 的中点,DE⊥AC. 则 AB : AE = __________.
4:1
1.如图,∠AOP=∠BOP=15°,PC∥OA 交 OB 于 C,PD⊥OA 于 D,若 PC=3,则 PD 等于 ( )
A.3 B.2
C.1.5 D.1
随堂练习
解析:如图,过点 P 作 PE⊥OB 于 E.
∵ PC∥OA,
∴∠PCE=∠AOB=∠AOP+∠BOP=30°.
又∵ PC=3,∴ PE=1.5.
∵∠AOP=∠BOP,PD⊥OA,
∴ PD=PE=1.5.
E
答案:C
2.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
A
B
C
M
N
分析:∵CM平分∠ACB,MN平分∠AMC,
∴∠NCM=∠BCM,∠AMN=∠CMN
∵MN//BC,
∴∠NMC=∠BCM,即∠NCM=∠BCM=∠AMN=∠CMN,
∵∠AMN=90°,
∴∠AMN=∠CMN =∠NCM=30°.
∴∠B=60°,
∵AN=1,
∴ NM=NC=2.
∴AC=AN+NC=3.
∴BC=2AC=6.
A
B
C
M
N
3. 在△ABC 中,∠C = 90°,∠B = 15°,DE 是 AB 的垂直平分线,
BE = 5,求 AC 的长.
解:连接 AE.
∵ DE 是 AB 的垂直平分线,
∴ BE = AE.
∴∠B = ∠EAB = 15°.
∴∠AEC = 30°.
∵∠C = 90°,
∴ AC = AE = BE = 2.5.
4. 如图,已知△ABC 是等边三角形,D,E 分别为 BC、AC 上的点,且 CD = AE,AD、BE 相交于点 P,BQ⊥AD 于点 Q, 求证:BP = 2PQ.
证明:∵△ABC 为等边三角形,
∴ AC = BC = AB,∠C =∠BAC = 60°.
∵ CD = AE,
∴△ADC≌△BEA (SAS).
∴∠CAD =∠ABE.
∵∠BAP +∠CAD = 60°,
∴∠BAP +∠ABE = 60°,即∠BPQ = 60°.
又∵ BQ⊥AD,
∴∠BQP = 90°.
∴∠PBQ = 30°.
∴ BP = 2PQ.
说出含 30° 角的直角三角形的性质.
你答对了吗?
在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八上数学同步精品课件
人教版八年级上册
第十三章 轴对称
第2课时 含 30°角的
直角三角形的性质
第三节 等腰三角形
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 探索并证明含30° 角的直角三角形的性质:在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
2.会应用含30° 角的直角三角形的性质进行有关的证明和计算.
学习目标
重点
难点
回顾等边三角形的性质和判定.
等边三角形
性质 1. 三条边相等
2. 三个内角都相等,都为60°
3. “三线合一”
4. 轴对称图形 ( 3条对称轴 )
判定 1. 定义 ( 三条边相等 )
2. 三个角相等
3. 有一个角是 60° 的等腰三角形
新课引入
将两个全等且含有 30° 角的三角尺摆放在一起. 你能借助这个图形,找到Rt△ABC 的直角边 BC 与斜边 AB 之间的数量关系吗?
发现:将两个全等且含 30° 角的三角尺拼在一起得到一个等边三角形,再利用这个图形的轴对称性,得出 BC = AB.
新知学习
证明:∵△ADC 是△ABC 的轴对称图形
∴AB = AD,∠BAD = 2 × 30° = 60°.
∴△ABD 是等边三角形.
∵AC⊥BD.
你还能用其他方法证明吗?
∴BC = CD = AB.
发现:BC = AB.
证明:
∵在△ABC 中,AC⊥BC,∠BAC = 30°
∴∠B = 60°.
延长 BC 到点 D,使得 BD = AB,连接 AD,
则△ABD 是等边三角形,
∴AC 也是 BD 边上的中线.
发现:BC = AB.
∴BC = BD = AB.
含 30° 角的直角三角形的性质:
归纳
在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
数学语言:
∵在 Rt△ABC 中,∠C = 90°,∠A = 30°,
∴BC = AB.
例1 下图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4m,∠A = 30°,立柱 BC,DE 要多长
解:∵DE⊥AC,BC⊥AC,∠A = 30°,
∴BC = AB,DE = AD.
∴BC = ×7.4 = 3.7(m) .
又 AD = AB,
∴DE = ×AD = ×3.7 = l.85(m).
答:立柱 BC 的长是 3.7 m,DE 的长是1.85 m.
1.三角形三个角的度数之 比为 1:2:3,它的最大边长等于 16 cm,则最小边长是 _______cm .
分析:设三角形三个角的度数分别为 k,2k,3k.
根据三角形内角和定理得,k + 2k + 3k = 180°,
解得 k = 30°, ∴3k = 90°.
由含 30° 角的直角三角形的性质,
8
∴最小边长等于 ×16 = 8 cm.
针对训练
分析:连接 AD,
∵AB = AC,D 是 BC 的中点,∴AD⊥BC.
∵∠BAC = 120°,∴∠B =∠C = 30°.
∵DE⊥AC,∴∠ADE = 30°.
在Rt△ADE 中,AD = 2AE,
在Rt△ABD 中,AB = 2AD = 4AE,
∴AB : AE = 4 : 1.
2.如图,在△ABC 中,AB = AC,∠BAC = 120°,D 是 BC 的中点,DE⊥AC. 则 AB : AE = __________.
4:1
1.如图,∠AOP=∠BOP=15°,PC∥OA 交 OB 于 C,PD⊥OA 于 D,若 PC=3,则 PD 等于 ( )
A.3 B.2
C.1.5 D.1
随堂练习
解析:如图,过点 P 作 PE⊥OB 于 E.
∵ PC∥OA,
∴∠PCE=∠AOB=∠AOP+∠BOP=30°.
又∵ PC=3,∴ PE=1.5.
∵∠AOP=∠BOP,PD⊥OA,
∴ PD=PE=1.5.
E
答案:C
2.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN//BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )
A.4 B.6 C. D.8
A
B
C
M
N
分析:∵CM平分∠ACB,MN平分∠AMC,
∴∠NCM=∠BCM,∠AMN=∠CMN
∵MN//BC,
∴∠NMC=∠BCM,即∠NCM=∠BCM=∠AMN=∠CMN,
∵∠AMN=90°,
∴∠AMN=∠CMN =∠NCM=30°.
∴∠B=60°,
∵AN=1,
∴ NM=NC=2.
∴AC=AN+NC=3.
∴BC=2AC=6.
A
B
C
M
N
3. 在△ABC 中,∠C = 90°,∠B = 15°,DE 是 AB 的垂直平分线,
BE = 5,求 AC 的长.
解:连接 AE.
∵ DE 是 AB 的垂直平分线,
∴ BE = AE.
∴∠B = ∠EAB = 15°.
∴∠AEC = 30°.
∵∠C = 90°,
∴ AC = AE = BE = 2.5.
4. 如图,已知△ABC 是等边三角形,D,E 分别为 BC、AC 上的点,且 CD = AE,AD、BE 相交于点 P,BQ⊥AD 于点 Q, 求证:BP = 2PQ.
证明:∵△ABC 为等边三角形,
∴ AC = BC = AB,∠C =∠BAC = 60°.
∵ CD = AE,
∴△ADC≌△BEA (SAS).
∴∠CAD =∠ABE.
∵∠BAP +∠CAD = 60°,
∴∠BAP +∠ABE = 60°,即∠BPQ = 60°.
又∵ BQ⊥AD,
∴∠BQP = 90°.
∴∠PBQ = 30°.
∴ BP = 2PQ.
说出含 30° 角的直角三角形的性质.
你答对了吗?
在直角三角形中, 如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
