2023-2024学年北师大版数学九年级上册 1.3 正方形的性质与判定 同步练习 (含解析)
文档属性
| 名称 | 2023-2024学年北师大版数学九年级上册 1.3 正方形的性质与判定 同步练习 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 442.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 20:01:49 | ||
图片预览



文档简介
1.3 正方形的性质与判定
基础
1.如图,四边形ABCD的对角线AC、BD互相平分,要使它成为正方形,需要添加的条件是( )
A.AB=CD B.AC=BD
C.AC⊥BD D.AC=BD且AC⊥BD
2.如图,在学习“四边形”一章时,小明的书上有一图因不小心被滴上墨水,看不清所印的字,请问被墨迹遮盖了的文字应是( )
A.四边形 B.梯形 C.矩形 D.筝形
3.下列命题错误的是( )
A.有一组邻边相等的平行四边形叫做正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
D.有一个角是直角的菱形是正方形
4.如图,要使平行四边形ABCD是正方形,需增加条件.在条件①AB=BC,②∠ABC=90 ,③AC=BD,④AC⊥BD中选取两个作为条件,不正确的是( )
A.①和② B.②和③ C.①和③ D.②和④
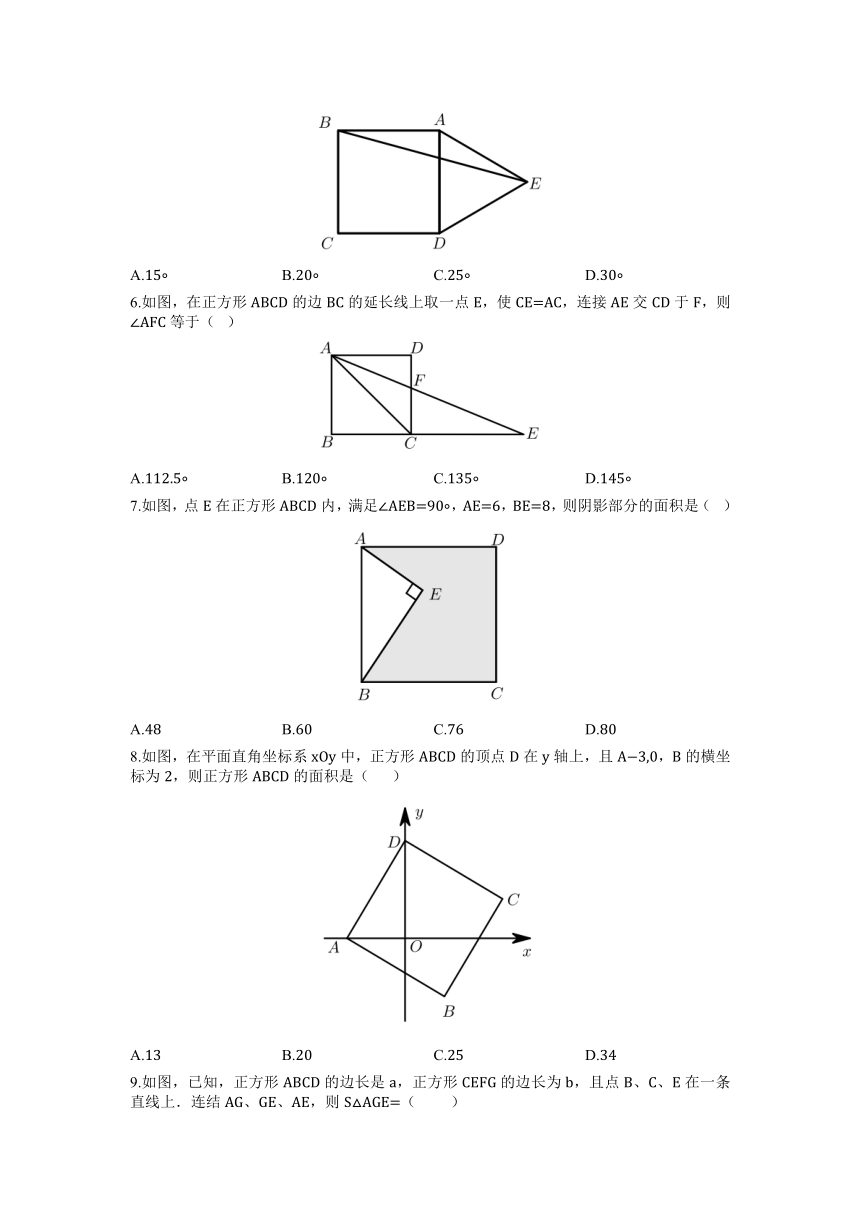
5.如图,在正方形ABCD的外侧,以AD为边作等边△ADE,连接BE,则∠AEB的度数为( )
A.15 B.20 C.25 D.30
6.如图,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连接AE交CD于F,则∠AFC等于( )
A.112.5 B.120 C.135 D.145
7.如图,点E在正方形ABCD内,满足∠AEB=90 ,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
8.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A 3,0,B的横坐标为2,则正方形ABCD的面积是( )
A.13 B.20 C.25 D.34
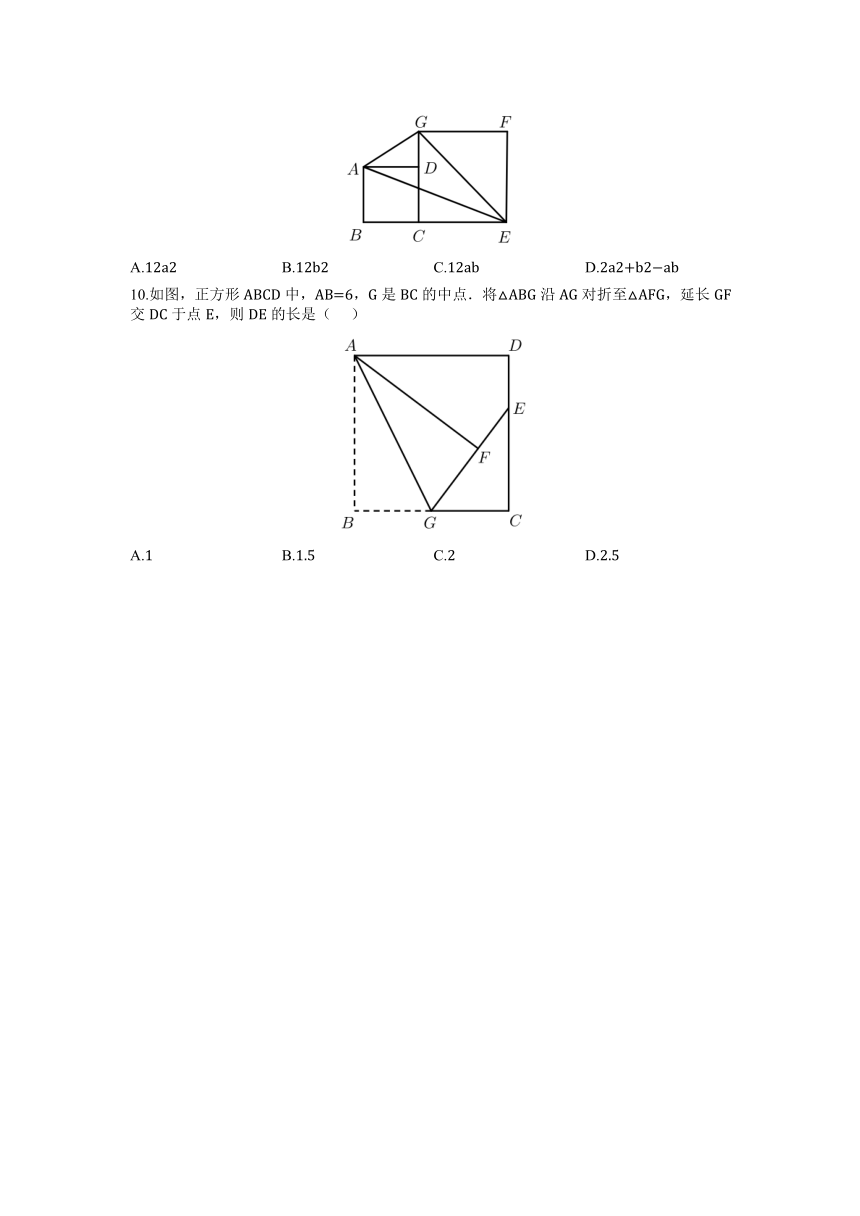
9.如图,已知,正方形ABCD的边长是a,正方形CEFG的边长为b,且点B、C、E在一条直线上.连结AG、GE、AE,则S△AGE=( )
A.12a2 B.12b2 C.12ab D.2a2+b2 ab
10.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
答案与解析
1.D
解析: 可添加AC=BD且AC⊥BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,
∵AC⊥BD,
∴矩形ABCD是正方形.
2.C
解析: 由四边形的性质与关系可知,四个角均为直角的菱形是正方形,长宽比为1:1的矩形是正方形,而矩形也是属于平行四边形的一种特殊四边形;同时,既是矩形,又是菱形的平行四边形是正方形,符合题意,所以被墨迹遮盖了的文字应是矩形.
故选C.
3.A
解析: ∵有一组邻边相等的平行四边形叫做菱形,∴A错误;
∵有一组邻边相等的矩形是正方形,∴B正确;
∵有一组邻边相等并且有一个角是直角的平行四边形叫做正方形,∴C正确;
∵有一个角是直角的菱形是正方形,∴D正确.
4.B
5.A
解析: 由题意易知AB=AE,∠BAE=∠BAD+∠DAE=90 +60 =150 ,
∴∠AEB=12180 ∠BAE=15 .
6.A
解析: ∵四边形ABCD为正方形,
∴∠ACD=90 ,
∴∠DCE=90 ,
又∵AC是正方形ABCD的对角线,
∴∠ACF=45 ,
∴∠ACE=∠DCE+∠ACF=135 ,
∵CE=CA,
∴∠FAC=∠E=12180 135 =22.5 .
∴∠AFD=∠FAC+∠ACF=22.5 +45 =67.5 ,
∴∠AFC=180 67.5 =112.5 .
故选:A.
7.C
解析: ∵∠AEB=90 ,AE=6,BE=8,
∴在Rt△ABE中,AB2=AE2+BE2=100,
∴S阴影=S正方形ABCD S△ABE=AB2 12×AE×BE=100 12×6×8=76.
8.D
解析: 过B作BH⊥x轴交于H点,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90 ,
∴∠DAO+∠BAH=90 ,
∠BAH+∠ABH=90 ,
∴∠DAO=∠ABH,
∵∠AOD=∠AHB=90 ,
∴△DAO≌△ABH,
∴OA=BH,AH=OD,
又∵A 3,0,B横坐标为2,
∴OA=3,OH=2,
∴OD=AH=5,
∴AD=OA2+OD2=32+52=34,
∴正方形ABCD的面积=34.
故选D.
9.B
解析: 用“等积变换”方法,如图,连结AC,易证AC//GE,
根据“平行线间的距离处处相等”,
可知△AGE和△CGE同底GE等高,
∴S△AGE=S△CEG=12b2,
故选B.
10.C
解析: 如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90 ,
在Rt△AFE和Rt△ADE中,∵AE=AEAF=AD,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6 x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:6 x2+9=x+32,
解得x=2.
则DE=2.
进阶
1.如图,D、E、F分别是△ABC的边BC、CA、AB上的点,且DE//BA,DF//CA.要使四边形AFDE是正方形,可增加条件( )
A.AF=AE B.∠A=90 C.AD⊥EF D.AF=AE且∠A=90
2.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:(1)∠E=22.5 ;(2)∠AFC=112.5 ;(3)∠ACE=135 ;(4)AC=CE;(5)AD:CE=1:2,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
3.在正方形ABCD中,E、F两点分别是BC、CD边上的点,若△AEF是边长为2的等边三角形,则正方形ABCD的边长是( )
A.3+12 B.2+32 C.2 D.3 12
4.如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF//BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为( )
A.3 B.23 C.13 D.4
5.如图,在边长为4的正方形ABCD内取一点E,使得BE=CE,连接ED、BD.BD与CE相交于点O,若∠EOD=75 ,则△BED的面积为( )
A.342 B.43 4 C.3+1 D.16 83
6.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为4,则线段DH长度的最小值是 .
A.25 2 B.25 C.25+2 D.4
7.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
A.5 B.4 C.3 D.2
8.如图,正方形ABCD的三个顶点A、B、D分别在长方形EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为5,10,则正方形ABCD的面积为 .
9.如图,面积为1的正方形ABCD中,M,N分别为AD,BC的中点,将C折至MN上,落在P点处,BQ为折痕,则以PQ为边长的正方形面积为 .
10.如图:CA=CB,CD=CE,∠ACB=∠DCE=90 ,M、N、G、H分别为AE、AB、BD、DE的中点.求证:四边形MNGH为正方形.
答案与解析
1.D
解析: ∵DE//BA,DF//CA,∴四边形AFDE是平行四边形,
故当平行四边形邻边相等且有一个角为直角时,四边形AFDE是正方形.
2.A
解析: ∵正方形ABCD,
∴AD=DC,AD//BC且∠DAC=∠ACD=45 ,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5 ,
∴∠E=22.5 ,(1)正确,
∵∠D=90 ,
∴∠AFC=90 +22.5 =112.5 ,(2)正确,
∵∠ACB=∠ACD=45 ,
∴∠ACE=135 (3)正确,
∵∠CAE=∠E=22.5 ,
∴AC=CE,(4)正确,
在Rt△ADC中,AD2+CD2=AC2,
∴2AD2=AC2,∴ADAC=12,∵AC=CE,
∴ADCE=12,(5)正确,
∴综上,正确的有5个,
选A.
3.A
解析: ∵由题意AE=AF,AB=AD,∠B=∠D,
∴△ADF≌△ABE,
∴BE=DF,
∴EC=FC,
由题意知∠C=90 ,
∴∠CFE=∠CEF=45 ,
∵EF=2,
∴EC=FC=1,
则在直角△AFD中得: AD2+AD 12=22,
解得AD=1+32.
4.C
解析: 解:连接FM、EM、CM,
∵四边形ABCD为正方形,
∴∠ABC=∠BCD=∠ADC=90 ,BC=CD,
∵EF//BC,
∴∠GFD=∠BCD=90 ,EF=BC,
∴EF=BC=DC,
∵∠BDC=12∠ADC=45 ,
∴△GFD是等腰直角三角形,
∵M是DG的中点,
∴FM=DM=MG,FM⊥DG,
∴∠GFM=∠CDM=45 ,
∴△EMF △CMDSAS,
∴EM=CM,
过M作MH⊥CD于点H,
由勾股定理得:BD=62+62=62,
EC=42+62=213,
∵∠EBG=45 ,
∴△EBG是等腰直角三角形,
∴EG=BE=4,
∴BG=42,
∴DM=2,
∴MH=DH=1,
∴CH=6 1=5,
∴CM=EM=12+52=26,
∵CE2=EM2+CM2,
∴∠EMC=90 ,
∵N是EC的中点,
∴MN=12EC=13;
故选C.
5.B
解析: 过点E作EF⊥CD于点F,
∵四边形ABCD是正方形,
∴∠DBC=45 ,∠BCD=90 ,BC=CD.
∵∠BOC+∠OBC+∠OCB=180 ,∠EOD=75 ,
∴∠OCB=180 75 45 =60 .
∵BE=CE,
∴△BCE是等边三角形,
∴EC=BC=4,
∴∠ECD=90 60 =30 .
∵EF⊥CD,
∴∠EFC=90 ,
∴EF=12EC=12×4=2,
∴S四边形BCDE=34 42+12×4×2=43+4,
∴S△BED=S四边形BCDE S△BCD=43+4 12×4×4=43 4.
故选B.
6.A
解析: 在正方形ABCD中,AB=AD=CD,
∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,AB=DC∠BAD=∠CDAAE=DF,
∴△ABE≌△DCFSAS,
∴∠ABE=∠DCF,
在△ADG和△CDG中,AD=CD∠ADG=∠CDGDG=DG,
∴△ADG≌△CDGSAS,
∴∠DCF=∠DAG,
∴∠ABE=∠DAG,
∵∠BAH+∠DAG=∠BAD=90 ,
∴∠ABE+∠BAH=90 ,
∴∠AHB=180 90 =90 ,
取AB的中点O,连接OH、OD(图略),
则OH=AO=12AB=2,
在Rt△AOD中,OD=AO2+AD2=25,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值为OD OH=25 2.
故选A.
7.B
解析: ①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=2PF=2CE;
⑤正确,PB2+PD2=2PA2.
故选B.
8.13
解析: 过点C作CP⊥HG于P,CM⊥EH于M,CN⊥FG于N,
连接CH,CG.
∵C到HG距离为1,CH=5,CG=10,
∴在Rt△CPH中,HP=52 12=2,
在Rt△CPG中,GP=102 12=3,
∴MC=2,CN=3,
∵四边形ABCD为正方形,
∴∠DCB=90 ,∠DCM+∠BCN=90 ,DC=BC,
又∵∠MDC+∠DCM=90 ,
∴∠MDC=∠BCN,
又∵∠DMC=∠CNB=90 ,
∴△DMC≌△CNB(AAS),
∴DM=CN=3,
在Rt△DMC中,DC=DM2+MC2=32+22=13,
∴S正ABCD=132=13.
故答案为13.
9.13
解析: ∵N为BC的中点,
∴BN=NC=12BC=12,
∴PB=PC,
∴PN⊥BC,
∴∠PNC=90 ,
∵折叠,
∴△PQB≌△CQB,
∴PB=CB=1,
∴PC=1,
∵在△PCN中,∠PNC=90 ,
∴PN2+NC2=PC2,
∴PN2+14=1,
∴PN=34即32,
∵四边形ABCD是正方形 ,
∴∠D=∠DCB=90 ,AD//BC,
∴∠MNC+∠NMD=180 ,
∴∠NMD=90 ,
∴四边形NMDC是矩形,
∴NM=DC=1,
∴MP=1 32,
∵CQ=PQ,作QH⊥PN,
∴QH=12,NH=CQ=PQ,
又∵PN=32,设PQ=CQ=NH=x,
∴x2 122=32 x2,
解得x=33,
∴S=332=13.
10.证明见解析.
解析: 连接AD、BF,
∵M、N分别为AE、AB中点,
∴MN为△ABE的中位线,则MN//BE,且MN=12BE,
同理可得:GH//BE,且GH=12BE,
NG=MH=12AD,NG//MH//AD,
∴四边形MNGH为平行四边形,
∵AC=BC,CD=CE,∠ACD=∠BCE=90 ,
∴△ACD≌△BCE,
∴AD=AE,
∴NG=MH=GH=MN,
∴四边形MNGH为菱形,
∵MH//AD,
∴∠EMH=∠EAD=∠EBC,
∵MN//BE,
∴∠BEC=∠NMC,
∵∠BEC+∠EBC=90 ,
∴∠NMC+∠EMH=90 ,
∴∠NMH=90 ,
∴四边形MNGH为正方形.
基础
1.如图,四边形ABCD的对角线AC、BD互相平分,要使它成为正方形,需要添加的条件是( )
A.AB=CD B.AC=BD
C.AC⊥BD D.AC=BD且AC⊥BD
2.如图,在学习“四边形”一章时,小明的书上有一图因不小心被滴上墨水,看不清所印的字,请问被墨迹遮盖了的文字应是( )
A.四边形 B.梯形 C.矩形 D.筝形
3.下列命题错误的是( )
A.有一组邻边相等的平行四边形叫做正方形
B.有一组邻边相等的矩形是正方形
C.有一组邻边相等并且有一个角是直角的平行四边形叫做正方形
D.有一个角是直角的菱形是正方形
4.如图,要使平行四边形ABCD是正方形,需增加条件.在条件①AB=BC,②∠ABC=90 ,③AC=BD,④AC⊥BD中选取两个作为条件,不正确的是( )
A.①和② B.②和③ C.①和③ D.②和④
5.如图,在正方形ABCD的外侧,以AD为边作等边△ADE,连接BE,则∠AEB的度数为( )
A.15 B.20 C.25 D.30
6.如图,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连接AE交CD于F,则∠AFC等于( )
A.112.5 B.120 C.135 D.145
7.如图,点E在正方形ABCD内,满足∠AEB=90 ,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
8.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A 3,0,B的横坐标为2,则正方形ABCD的面积是( )
A.13 B.20 C.25 D.34
9.如图,已知,正方形ABCD的边长是a,正方形CEFG的边长为b,且点B、C、E在一条直线上.连结AG、GE、AE,则S△AGE=( )
A.12a2 B.12b2 C.12ab D.2a2+b2 ab
10.如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
答案与解析
1.D
解析: 可添加AC=BD且AC⊥BD,理由如下:
∵四边形ABCD的对角线互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴平行四边形ABCD是矩形,
∵AC⊥BD,
∴矩形ABCD是正方形.
2.C
解析: 由四边形的性质与关系可知,四个角均为直角的菱形是正方形,长宽比为1:1的矩形是正方形,而矩形也是属于平行四边形的一种特殊四边形;同时,既是矩形,又是菱形的平行四边形是正方形,符合题意,所以被墨迹遮盖了的文字应是矩形.
故选C.
3.A
解析: ∵有一组邻边相等的平行四边形叫做菱形,∴A错误;
∵有一组邻边相等的矩形是正方形,∴B正确;
∵有一组邻边相等并且有一个角是直角的平行四边形叫做正方形,∴C正确;
∵有一个角是直角的菱形是正方形,∴D正确.
4.B
5.A
解析: 由题意易知AB=AE,∠BAE=∠BAD+∠DAE=90 +60 =150 ,
∴∠AEB=12180 ∠BAE=15 .
6.A
解析: ∵四边形ABCD为正方形,
∴∠ACD=90 ,
∴∠DCE=90 ,
又∵AC是正方形ABCD的对角线,
∴∠ACF=45 ,
∴∠ACE=∠DCE+∠ACF=135 ,
∵CE=CA,
∴∠FAC=∠E=12180 135 =22.5 .
∴∠AFD=∠FAC+∠ACF=22.5 +45 =67.5 ,
∴∠AFC=180 67.5 =112.5 .
故选:A.
7.C
解析: ∵∠AEB=90 ,AE=6,BE=8,
∴在Rt△ABE中,AB2=AE2+BE2=100,
∴S阴影=S正方形ABCD S△ABE=AB2 12×AE×BE=100 12×6×8=76.
8.D
解析: 过B作BH⊥x轴交于H点,
∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90 ,
∴∠DAO+∠BAH=90 ,
∠BAH+∠ABH=90 ,
∴∠DAO=∠ABH,
∵∠AOD=∠AHB=90 ,
∴△DAO≌△ABH,
∴OA=BH,AH=OD,
又∵A 3,0,B横坐标为2,
∴OA=3,OH=2,
∴OD=AH=5,
∴AD=OA2+OD2=32+52=34,
∴正方形ABCD的面积=34.
故选D.
9.B
解析: 用“等积变换”方法,如图,连结AC,易证AC//GE,
根据“平行线间的距离处处相等”,
可知△AGE和△CGE同底GE等高,
∴S△AGE=S△CEG=12b2,
故选B.
10.C
解析: 如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90 ,
在Rt△AFE和Rt△ADE中,∵AE=AEAF=AD,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6 x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:6 x2+9=x+32,
解得x=2.
则DE=2.
进阶
1.如图,D、E、F分别是△ABC的边BC、CA、AB上的点,且DE//BA,DF//CA.要使四边形AFDE是正方形,可增加条件( )
A.AF=AE B.∠A=90 C.AD⊥EF D.AF=AE且∠A=90
2.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:(1)∠E=22.5 ;(2)∠AFC=112.5 ;(3)∠ACE=135 ;(4)AC=CE;(5)AD:CE=1:2,其中正确的有( )
A.5个 B.4个 C.3个 D.2个
3.在正方形ABCD中,E、F两点分别是BC、CD边上的点,若△AEF是边长为2的等边三角形,则正方形ABCD的边长是( )
A.3+12 B.2+32 C.2 D.3 12
4.如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF//BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为( )
A.3 B.23 C.13 D.4
5.如图,在边长为4的正方形ABCD内取一点E,使得BE=CE,连接ED、BD.BD与CE相交于点O,若∠EOD=75 ,则△BED的面积为( )
A.342 B.43 4 C.3+1 D.16 83
6.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于点H.若正方形的边长为4,则线段DH长度的最小值是 .
A.25 2 B.25 C.25+2 D.4
7.如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
A.5 B.4 C.3 D.2
8.如图,正方形ABCD的三个顶点A、B、D分别在长方形EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为5,10,则正方形ABCD的面积为 .
9.如图,面积为1的正方形ABCD中,M,N分别为AD,BC的中点,将C折至MN上,落在P点处,BQ为折痕,则以PQ为边长的正方形面积为 .
10.如图:CA=CB,CD=CE,∠ACB=∠DCE=90 ,M、N、G、H分别为AE、AB、BD、DE的中点.求证:四边形MNGH为正方形.
答案与解析
1.D
解析: ∵DE//BA,DF//CA,∴四边形AFDE是平行四边形,
故当平行四边形邻边相等且有一个角为直角时,四边形AFDE是正方形.
2.A
解析: ∵正方形ABCD,
∴AD=DC,AD//BC且∠DAC=∠ACD=45 ,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5 ,
∴∠E=22.5 ,(1)正确,
∵∠D=90 ,
∴∠AFC=90 +22.5 =112.5 ,(2)正确,
∵∠ACB=∠ACD=45 ,
∴∠ACE=135 (3)正确,
∵∠CAE=∠E=22.5 ,
∴AC=CE,(4)正确,
在Rt△ADC中,AD2+CD2=AC2,
∴2AD2=AC2,∴ADAC=12,∵AC=CE,
∴ADCE=12,(5)正确,
∴综上,正确的有5个,
选A.
3.A
解析: ∵由题意AE=AF,AB=AD,∠B=∠D,
∴△ADF≌△ABE,
∴BE=DF,
∴EC=FC,
由题意知∠C=90 ,
∴∠CFE=∠CEF=45 ,
∵EF=2,
∴EC=FC=1,
则在直角△AFD中得: AD2+AD 12=22,
解得AD=1+32.
4.C
解析: 解:连接FM、EM、CM,
∵四边形ABCD为正方形,
∴∠ABC=∠BCD=∠ADC=90 ,BC=CD,
∵EF//BC,
∴∠GFD=∠BCD=90 ,EF=BC,
∴EF=BC=DC,
∵∠BDC=12∠ADC=45 ,
∴△GFD是等腰直角三角形,
∵M是DG的中点,
∴FM=DM=MG,FM⊥DG,
∴∠GFM=∠CDM=45 ,
∴△EMF △CMDSAS,
∴EM=CM,
过M作MH⊥CD于点H,
由勾股定理得:BD=62+62=62,
EC=42+62=213,
∵∠EBG=45 ,
∴△EBG是等腰直角三角形,
∴EG=BE=4,
∴BG=42,
∴DM=2,
∴MH=DH=1,
∴CH=6 1=5,
∴CM=EM=12+52=26,
∵CE2=EM2+CM2,
∴∠EMC=90 ,
∵N是EC的中点,
∴MN=12EC=13;
故选C.
5.B
解析: 过点E作EF⊥CD于点F,
∵四边形ABCD是正方形,
∴∠DBC=45 ,∠BCD=90 ,BC=CD.
∵∠BOC+∠OBC+∠OCB=180 ,∠EOD=75 ,
∴∠OCB=180 75 45 =60 .
∵BE=CE,
∴△BCE是等边三角形,
∴EC=BC=4,
∴∠ECD=90 60 =30 .
∵EF⊥CD,
∴∠EFC=90 ,
∴EF=12EC=12×4=2,
∴S四边形BCDE=34 42+12×4×2=43+4,
∴S△BED=S四边形BCDE S△BCD=43+4 12×4×4=43 4.
故选B.
6.A
解析: 在正方形ABCD中,AB=AD=CD,
∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,AB=DC∠BAD=∠CDAAE=DF,
∴△ABE≌△DCFSAS,
∴∠ABE=∠DCF,
在△ADG和△CDG中,AD=CD∠ADG=∠CDGDG=DG,
∴△ADG≌△CDGSAS,
∴∠DCF=∠DAG,
∴∠ABE=∠DAG,
∵∠BAH+∠DAG=∠BAD=90 ,
∴∠ABE+∠BAH=90 ,
∴∠AHB=180 90 =90 ,
取AB的中点O,连接OH、OD(图略),
则OH=AO=12AB=2,
在Rt△AOD中,OD=AO2+AD2=25,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值为OD OH=25 2.
故选A.
7.B
解析: ①正确,连接PC,可得PC=EF,PC=PA,∴AP=EF;
②正确;延长AP,交EF于点N,则∠EPN=∠BAP=∠PCE=∠PFE,可得AP⊥EF;
③正确;∠PFE=∠PCE=∠BAP;
④错误,PD=2PF=2CE;
⑤正确,PB2+PD2=2PA2.
故选B.
8.13
解析: 过点C作CP⊥HG于P,CM⊥EH于M,CN⊥FG于N,
连接CH,CG.
∵C到HG距离为1,CH=5,CG=10,
∴在Rt△CPH中,HP=52 12=2,
在Rt△CPG中,GP=102 12=3,
∴MC=2,CN=3,
∵四边形ABCD为正方形,
∴∠DCB=90 ,∠DCM+∠BCN=90 ,DC=BC,
又∵∠MDC+∠DCM=90 ,
∴∠MDC=∠BCN,
又∵∠DMC=∠CNB=90 ,
∴△DMC≌△CNB(AAS),
∴DM=CN=3,
在Rt△DMC中,DC=DM2+MC2=32+22=13,
∴S正ABCD=132=13.
故答案为13.
9.13
解析: ∵N为BC的中点,
∴BN=NC=12BC=12,
∴PB=PC,
∴PN⊥BC,
∴∠PNC=90 ,
∵折叠,
∴△PQB≌△CQB,
∴PB=CB=1,
∴PC=1,
∵在△PCN中,∠PNC=90 ,
∴PN2+NC2=PC2,
∴PN2+14=1,
∴PN=34即32,
∵四边形ABCD是正方形 ,
∴∠D=∠DCB=90 ,AD//BC,
∴∠MNC+∠NMD=180 ,
∴∠NMD=90 ,
∴四边形NMDC是矩形,
∴NM=DC=1,
∴MP=1 32,
∵CQ=PQ,作QH⊥PN,
∴QH=12,NH=CQ=PQ,
又∵PN=32,设PQ=CQ=NH=x,
∴x2 122=32 x2,
解得x=33,
∴S=332=13.
10.证明见解析.
解析: 连接AD、BF,
∵M、N分别为AE、AB中点,
∴MN为△ABE的中位线,则MN//BE,且MN=12BE,
同理可得:GH//BE,且GH=12BE,
NG=MH=12AD,NG//MH//AD,
∴四边形MNGH为平行四边形,
∵AC=BC,CD=CE,∠ACD=∠BCE=90 ,
∴△ACD≌△BCE,
∴AD=AE,
∴NG=MH=GH=MN,
∴四边形MNGH为菱形,
∵MH//AD,
∴∠EMH=∠EAD=∠EBC,
∵MN//BE,
∴∠BEC=∠NMC,
∵∠BEC+∠EBC=90 ,
∴∠NMC+∠EMH=90 ,
∴∠NMH=90 ,
∴四边形MNGH为正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
