2023-2024学年人教版数学八年级上册 11.3.2 多边形的内角和同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册 11.3.2 多边形的内角和同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 519.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 08:00:26 | ||
图片预览

文档简介
11.3.2 多边形的内角和
一、选择题(共7小题)
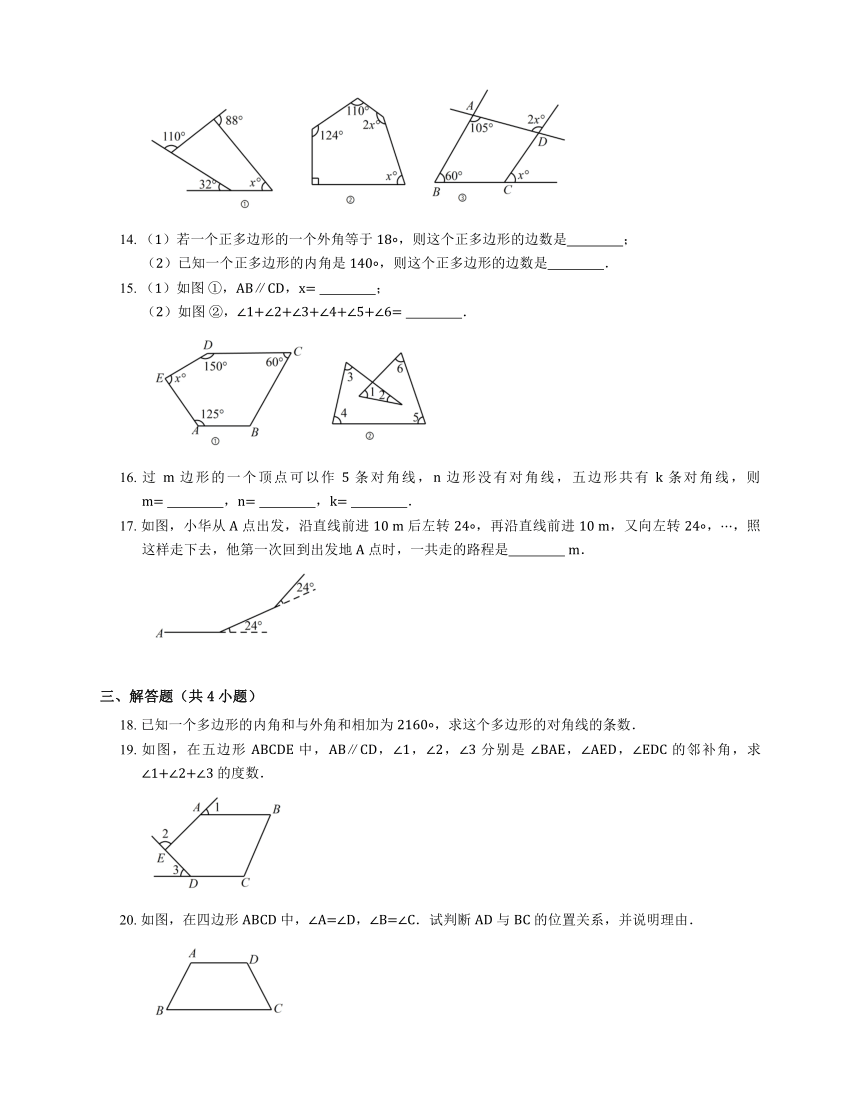
1. 在如图所示的图形中,凸多边形共有
A. 1 个 B. 2 个 C. 3 个 D. 4 个
2. 若一个多边形的内角和是 900 ,则这个多边形是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
3. 若一个多边形的外角和与它的内角和相等,则这个多边形是 .
A. 三角形 B. 四边形 C. 五边形 D. 六边形
4. 将一个 n 边形变成 n+1 边形,内角和将
A. 减少 180 B. 增加 90 C. 增加 180 D. 增加 360
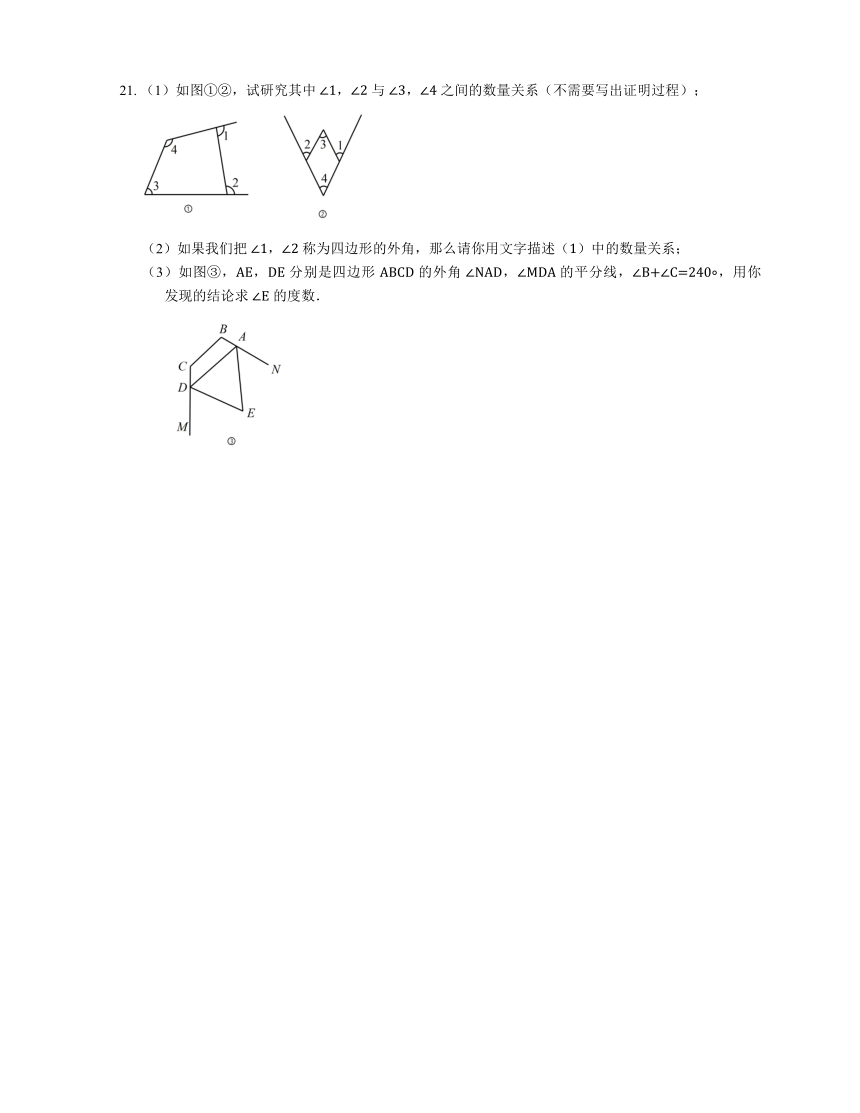
5. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是
A. 360 B. 540 C. 720 D. 900
6. 从一个 n 边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成 6 个三角形,则 n 的值是
A. 6 B. 7 C. 8 D. 9
7. 一个多边形除了一个内角外,其余各内角的和为 2000 ,则这个内角的度数为
A. 20 B. 160 C. 200 D. 140
二、填空题(共10小题)
8. 在平面内,由一些线段 相接组成的封闭图形叫做多边形;多边形 组成的角叫做多边形的内角;多边形的边与它的 组成的角叫做多边形的外角.
9. 连接多边形 的两个顶点的线段,叫做多边形的对角线.从 n 边形 n≥4 的一个顶点出发,可以作 条对角线,这些对角线将 n 边形分为 个三角形;n 边形共有 条对角线.
10. 画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的 ,那么这个多边形就叫做凸多边形.
11. 都相等, 都相等的多边形叫做正多边形.
12. n 边形的内角和等于 ;多边形的外角和等于 .
13. (1)如图①,x= ;如图②,x= ;(3)如图③,x= .
14. (1)若一个正多边形的一个外角等于 18 ,则这个正多边形的边数是 ;
(2)已知一个正多边形的内角是 140 ,则这个正多边形的边数是 .
15. (1)如图 ①,AB∥CD,x= ;
(2)如图 ②,∠1+∠2+∠3+∠4+∠5+∠6= .
16. 过 m 边形的一个顶点可以作 5 条对角线,n 边形没有对角线,五边形共有 k 条对角线,则 m= ,n= ,k= .
17. 如图,小华从 A 点出发,沿直线前进 10 m 后左转 24 ,再沿直线前进 10 m,又向左转 24 , ,照这样走下去,他第一次回到出发地 A 点时,一共走的路程是 m.
三、解答题(共4小题)
18. 已知一个多边形的内角和与外角和相加为 2160 ,求这个多边形的对角线的条数.
19. 如图,在五边形 ABCDE 中,AB∥CD,∠1,∠2,∠3 分别是 ∠BAE,∠AED,∠EDC 的邻补角,求 ∠1+∠2+∠3 的度数.
20. 如图,在四边形 ABCD 中,∠A=∠D,∠B=∠C.试判断 AD 与 BC 的位置关系,并说明理由.
21. (1)如图①②,试研究其中 ∠1,∠2 与 ∠3,∠4 之间的数量关系(不需要写出证明过程);
(2)如果我们把 ∠1,∠2 称为四边形的外角,那么请你用文字描述(1)中的数量关系;
(3)如图③,AE,DE 分别是四边形 ABCD 的外角 ∠NAD,∠MDA 的平分线,∠B+∠C=240 ,用你发现的结论求 ∠E 的度数.
答案
1. B
2. C
3. B
4. C
5. D
6. C
7. B
8. 首尾顺次,相邻两边,邻边的延长线
9. 不相邻,n 3,n 2,nn 32
10. 同一侧
11. 各个角,各条边
12. n 2×180 ,360
13. 50,72,55
14. 20,9
15. 85,360
16. 8,3,5
17. 150
18. 设这个多边形的边数为 n.
由题意,得
n 2×180 +360 =2160 ,
解得
n=12.∴
12nn 3=54.
∴ 这个多边形的对角线的条数为 54.
19. 如图,延长 AB,DC,
则 ∠4,∠5 分别是 ∠ABC,∠BCD 的邻补角.
∵ AB∥CD,
∴ ∠4+∠5=180 .
又 ∵ ∠1+∠2+∠3+∠4+∠5=360 ,
∴ ∠1+∠2+∠3=360 ∠4+∠5=360 180 =180 .
20. AD∥BC.
理由:∵ ∠A+∠B+∠C+∠D=360 ,∠A=∠D,∠B=∠C,
∴ 2∠A+∠B=360 .
∴ ∠A+∠B=180 .
∴ AD∥BC.
21. (1) ∠1+∠2=∠3+∠4.
(2) 四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3) ∵ ∠B+∠C=240 ,
∴ ∠MDA+∠NAD=240 .
∵ AE,DE 分别是 ∠NAD,∠MDA 的平分线,
∴ ∠ADE=12∠MDA,∠DAE=12∠NAD.
∴ ∠ADE+∠DAE=12∠MDA+∠NAD=120 .
∴ ∠E=180 ∠ADE+∠DAE=60 .
一、选择题(共7小题)
1. 在如图所示的图形中,凸多边形共有
A. 1 个 B. 2 个 C. 3 个 D. 4 个
2. 若一个多边形的内角和是 900 ,则这个多边形是
A. 五边形 B. 六边形 C. 七边形 D. 八边形
3. 若一个多边形的外角和与它的内角和相等,则这个多边形是 .
A. 三角形 B. 四边形 C. 五边形 D. 六边形
4. 将一个 n 边形变成 n+1 边形,内角和将
A. 减少 180 B. 增加 90 C. 增加 180 D. 增加 360
5. 将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和之和不可能是
A. 360 B. 540 C. 720 D. 900
6. 从一个 n 边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成 6 个三角形,则 n 的值是
A. 6 B. 7 C. 8 D. 9
7. 一个多边形除了一个内角外,其余各内角的和为 2000 ,则这个内角的度数为
A. 20 B. 160 C. 200 D. 140
二、填空题(共10小题)
8. 在平面内,由一些线段 相接组成的封闭图形叫做多边形;多边形 组成的角叫做多边形的内角;多边形的边与它的 组成的角叫做多边形的外角.
9. 连接多边形 的两个顶点的线段,叫做多边形的对角线.从 n 边形 n≥4 的一个顶点出发,可以作 条对角线,这些对角线将 n 边形分为 个三角形;n 边形共有 条对角线.
10. 画出多边形的任何一条边所在直线,如果整个多边形都在这条直线的 ,那么这个多边形就叫做凸多边形.
11. 都相等, 都相等的多边形叫做正多边形.
12. n 边形的内角和等于 ;多边形的外角和等于 .
13. (1)如图①,x= ;如图②,x= ;(3)如图③,x= .
14. (1)若一个正多边形的一个外角等于 18 ,则这个正多边形的边数是 ;
(2)已知一个正多边形的内角是 140 ,则这个正多边形的边数是 .
15. (1)如图 ①,AB∥CD,x= ;
(2)如图 ②,∠1+∠2+∠3+∠4+∠5+∠6= .
16. 过 m 边形的一个顶点可以作 5 条对角线,n 边形没有对角线,五边形共有 k 条对角线,则 m= ,n= ,k= .
17. 如图,小华从 A 点出发,沿直线前进 10 m 后左转 24 ,再沿直线前进 10 m,又向左转 24 , ,照这样走下去,他第一次回到出发地 A 点时,一共走的路程是 m.
三、解答题(共4小题)
18. 已知一个多边形的内角和与外角和相加为 2160 ,求这个多边形的对角线的条数.
19. 如图,在五边形 ABCDE 中,AB∥CD,∠1,∠2,∠3 分别是 ∠BAE,∠AED,∠EDC 的邻补角,求 ∠1+∠2+∠3 的度数.
20. 如图,在四边形 ABCD 中,∠A=∠D,∠B=∠C.试判断 AD 与 BC 的位置关系,并说明理由.
21. (1)如图①②,试研究其中 ∠1,∠2 与 ∠3,∠4 之间的数量关系(不需要写出证明过程);
(2)如果我们把 ∠1,∠2 称为四边形的外角,那么请你用文字描述(1)中的数量关系;
(3)如图③,AE,DE 分别是四边形 ABCD 的外角 ∠NAD,∠MDA 的平分线,∠B+∠C=240 ,用你发现的结论求 ∠E 的度数.
答案
1. B
2. C
3. B
4. C
5. D
6. C
7. B
8. 首尾顺次,相邻两边,邻边的延长线
9. 不相邻,n 3,n 2,nn 32
10. 同一侧
11. 各个角,各条边
12. n 2×180 ,360
13. 50,72,55
14. 20,9
15. 85,360
16. 8,3,5
17. 150
18. 设这个多边形的边数为 n.
由题意,得
n 2×180 +360 =2160 ,
解得
n=12.∴
12nn 3=54.
∴ 这个多边形的对角线的条数为 54.
19. 如图,延长 AB,DC,
则 ∠4,∠5 分别是 ∠ABC,∠BCD 的邻补角.
∵ AB∥CD,
∴ ∠4+∠5=180 .
又 ∵ ∠1+∠2+∠3+∠4+∠5=360 ,
∴ ∠1+∠2+∠3=360 ∠4+∠5=360 180 =180 .
20. AD∥BC.
理由:∵ ∠A+∠B+∠C+∠D=360 ,∠A=∠D,∠B=∠C,
∴ 2∠A+∠B=360 .
∴ ∠A+∠B=180 .
∴ AD∥BC.
21. (1) ∠1+∠2=∠3+∠4.
(2) 四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3) ∵ ∠B+∠C=240 ,
∴ ∠MDA+∠NAD=240 .
∵ AE,DE 分别是 ∠NAD,∠MDA 的平分线,
∴ ∠ADE=12∠MDA,∠DAE=12∠NAD.
∴ ∠ADE+∠DAE=12∠MDA+∠NAD=120 .
∴ ∠E=180 ∠ADE+∠DAE=60 .
