第二章 一元二次方程 章节课后练习(无答案)北师大版数学九年级上册
文档属性
| 名称 | 第二章 一元二次方程 章节课后练习(无答案)北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 22:46:00 | ||
图片预览



文档简介
第二章 一元二次方程
一元二次方程
1.下列方程属于一元二次方程的是( )
A.x3+x2+2=0 B.y=5-x
C.x+=5 D.x2+2x=3
2.把方程x2-3(x+1)=2x化成一般形式正确的是( )
A.x2-x-3=0 B.x2+x+3=0
C.x2-5x-3=0 D.x2-5x+3=0
3.将方程x2-2=7x化成x2+bx+c=0的形式,则一次项是 -7x,b+c=-9.
4.若关于x的一元二次方程(m-2)x2-x+m2-4=0的常数项为0,则m的值为-2.
5.一个直角三角形的两条直角边相差3 cm,面积是9 cm2,设较长的直角边的长为x cm,根据题意,可列方程为 x(x-3)=9.
6.若已知两个数的积为12,和为7,设其中一个数为x,则依题意可列方程x(7-x)=12.
7.设a是二次项系数,b是一次项系数,c是常数项,且满足(a-3)2++=0,求满足条件的一元二次方程.
一元二次方程的解
1.已知x=2是方程x2-2x+c=0的一个根,则实数c的值是( )
A.-1 B.0
C.1 D.2
2.写出有一个根为x=1的一元二次方程,它可以是x2-1=0(答案不唯一).
3.根据下表确定一元二次方程x2+2x-9=0的一个解的范围是2<x<3.
x 0 1 2 3 4
x2+2x-9 -9 -6 -1 6 15
4.根据下列表格的对应值:
x 2.4 2.5 2.6 2.7
ax2+bx+c(近似值) 5.6 5.7 5.8 5.9
判断方程ax2+bx+c=5.78(a≠0,a,b,c为常数)的一个近似解是( )
A.2.41 B.2.57
C.2.63 D.2.67
5.在一元二次方程ax2+bx+c=0中,若a,b,c满足关系式a-b+c=0,则这个方程必有一个根为x=-1.
6.已知x=-1是方程x2+ax-b=0的一个根,求a2-b2+2b的值.
7.将方程4x2+8x=25化成ax2+bx+c=0的形式,则a,b,c的值分别为( )
A.4,8,25 B.4,-8,-25
C.4,8,-25 D.4,-8,25
解一元二次方程(直接开方法)
1.一元二次方程x2=4的根为( )
A.x1=x2=2 B.x1=x2=-2
C.x1=2,x2=-2 D.x1=4,x2=-4
2.若关于x的方程4x2=m有实数根,则m的取值范围是( )
A.m>0 B.m≥0
C.m<0 D.m≤0
3.方程(x-2)2+4=0的解是( )
A.x1=x2=0 B.x1=2,x2=-2
C.x1=0,x2=4 D.没有实数根
4.一元二次方程3x2-75=0的解为x1=5,x2=-5.
5.解方程:
(1)(x+1)2-25=0;
(2)(2x-5)2=9.
6.若一元二次方程ax2+bx+1=0的一根为x=3,则3a+b的值为- .
解一元二次方程(配方法)
1.用配方法解一元二次方程x2+3x=1时,应在等式两边都加上 .
2.一元二次方程x2-6x+5=0配方后可变形为( )
A.(x-3)2=14 B.(x-3)2=4
C.(x+3)2=14 D.(x+3)2=4
3.用配方法解一元二次方程2x2-3x-1=0,配方正确的是( )
A.(x-)2= B.(x-)2=
C.(x-)2= D.(x-)2=
4.用配方法将方程x2-2x-3=0化成(x-a)2=b的形式,则a+b=5.
5.解方程:
(1)x2+4x-2=0; (2)3x2-6x+1=0.
6.解方程:2(x-1)2-50=0.
解一元二次方程(公式法)
1.用公式法解方程x2+x=2时,求根公式中的a,b,c的值分别是( )
A.a=1,b=1,c=2 B.a=1,b=-1,c=-2
C.a=1,b=1,c=-2 D.a=1,b=-1,c=2
2.用公式法解方程4x2-12x=3时,Δ的值是( )
A.-8 B.8
C.-192 D.192
3.用公式法解方程:2x2-x-1=0.
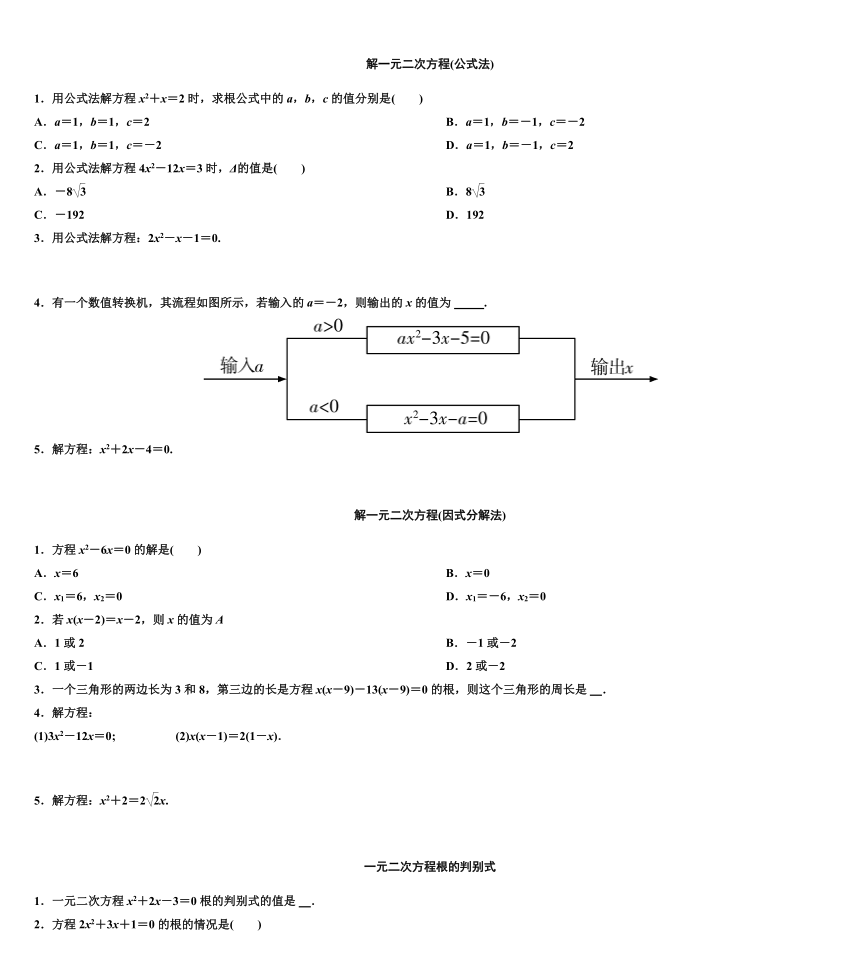
4.有一个数值转换机,其流程如图所示,若输入的a=-2,则输出的x的值为1或2.
5.解方程:x2+2x-4=0.
解一元二次方程(因式分解法)
1.方程x2-6x=0的解是( )
A.x=6 B.x=0
C.x1=6,x2=0 D.x1=-6,x2=0
2.若x(x-2)=x-2,则x的值为A
A.1或2 B.-1或-2
C.1或-1 D.2或-2
3.一个三角形的两边长为3和8,第三边的长是方程x(x-9)-13(x-9)=0的根,则这个三角形的周长是20.
4.解方程:
(1)3x2-12x=0; (2)x(x-1)=2(1-x).
5.解方程:x2+2=2x.
一元二次方程根的判别式
1.一元二次方程x2+2x-3=0根的判别式的值是16.
2.方程2x2+3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
3.(2022 丹东)关于x的一元二次方程x2+3x+m=0没有实数根,则m的取值范围是 m> .
4.(2022 西藏)已知关于x的一元二次方程(m-1)x2+2x-3=0有实数根,则m的取值范围是( )
A.m≥ B.m<
C.m>且m≠1 D.m≥且m≠1
5.若关于x的一元二次方程(m-1)x2-2(m-1)x+1=0有两个相等的实数根,则m的值是( )
A.0 B.1
C.2 D.1或2
6.解方程:
(1)x2+4x-21=0; (2)x(x-5)=2x-10.
一元二次方程的根与系数的关系
1.一元二次方程x2-5x+4=0的两根之和为( )
A.-5 B.5
C.-4 D.4
2.若一元二次方程x2-5x-7=0有两实数根x1和x2,则下列选项正确的是( )
A.x1+x2=-5 B.x1x2=7
C.x1=x2 D.x1x2-x1-x2=-12
3.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1 x2=1,则ba的值是A
A. B.-
C.4 D.-1
4.已知x=3是关于x的一元二次方程x2-2x-m=0的根,则该方程的另一个根是-1.
5.已知m,n是一元二次方程x2+4x-2=0的两根,则代数式(m+1)(n+1)的值等于-5.
6.已知关于x的一元二次方程x2-4x+k-1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x+x=10,求k的值.
实际问题与一元二次方程(1)——面积问题
1.用一块长80 cm,宽60 cm的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为1 500 cm2的无盖长方体纸盒,设截去的小正方形的边长为x cm,则可列方程为(80-2x)(60-2x)=1 500.
2.如图所示,把四个长和宽分别为x+2和x的矩形拼接成大正方形.若四个矩形和中间小正方形的面积和为4×35+22,则根据题意能列出的方程是A
A.x2+2x-35=0 B.x2+2x+35=0
C.x2+2x-4=0 D.x2+2x+4=0
第2题图
第3题图
3.如图,幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度.
4.等腰三角形的底边长为7,腰长是方程x2-9x+18=0的一个根,则这个等腰三角形的周长为19.
实际问题与一元二次方程(2)——面积问题
1.如图,幼儿园计划用30 m的围栏靠墙围成一个面积为100 m2的矩形小花园(墙长为15 m),则与墙垂直的边x为( )
A.10 m或5 m B.5 m或8 m
C.10 m D.5 m
2.如图所示,某建筑工地要靠一堵院墙围建一个面积为150 m2的矩形临时仓库.已知可利用的院墙长18 m,要求在与院墙平行的一边开一个宽为2 m的门,现有的砖料按要求只能砌成33 m长的围墙,求这个待建临时仓库的长和宽.
3.设a,b是方程x2+x-2 023=0的两个实数根,则ab+a+b的值是-2 024.
实际问题与一元二次方程(3)——增长率问题
1.某旅游景点10月份共接待游客64万人次,12月份共接待游客25万人次,设每月游客人数的平均下降率为x,则下列方程正确的是( )
A.25(1+x)2=64 B.25(1+x2)=64
C.64(1-x)2=25 D.64(1-x2)=25
2.有种传染病蔓延极快,现有一人患有此病,两天后共有144人患病,则平均每天一人传染的人数为( )
A.9 B.10
C.11 D.12
3.某公司2020年盈利1 500万元,到2022年盈利2 160万元,假设每年盈利的年增长率相同.
(1)求该公司每年盈利的年增长率;
(2)若该公司每年盈利的年增长率不变,预计2023年盈利多少万元?
4.若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为24.
实际问题与一元二次方程(4)——互赠、握手问题
1.某生物兴趣小组的同学,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了72件,如果全组有x名同学,则根据题意列出方程是x(x-1)=72.
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了21条航线,则这个航空公司共有飞机场( )
A.4个 B.5个
C.6个 D.7个
3.某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
4.某电影因质量很高受到全国观众的喜爱,上映第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达10亿元,若把增长率记作x,则方程可以列为( )
A.3(1+x)=10
B.3(1+x)2=10
C.3+3(1+x)2=10
D.3+3(1+x)+3(1+x)2=10
实际问题与一元二次方程(5)——营销问题
1.某戏院举办文艺演出,经调研,当票价每张30元时,1 200张门票可以全部售出.票价每增加1元,售出的门票就减少20张,若涨价后,门票总收入达到38 500元,设票价每张x元,则可列方程为( )
A.x(1 200-20x)=38 500
B.x=38 500
C.(x-30)(1 200-20x)=38 500
D.(x-30)=38 500
2.在商场中,某运动品牌的鞋子,每天可销售20双,每双可获利40元.为庆祝新年,对该鞋子进行促销活动,该鞋子每双降价1元,平均每天可多售出2双.若设该鞋子每双每降价x元,请解答下列问题:
(1)用含x的代数式表示:降价x元后,每售出一双该鞋子可获得利润(40-x)元,平均每天可售出(20+2x)双该鞋子;
(2)在此次促销活动中,每双鞋子降价多少元,可使该品牌的鞋子每天盈利1 250元?
3.若一元二次方程x2-2x+a=0有一根为-1,则另一根为( )
A.5 B.-3
C.4 D.3
第二章复习
1.将一元二次方程2x2-1=x化成一般形式后,二次项系数和一次项系数分别是( )
A.-2,-1 B.2,0
C.2,1 D.2,-1
2.若x1,x2是一元二次方程x2-3x-2=0的两个根,则x1x2的值是( )
A.3 B.-2
C.-3 D.2
3.方程x2-x+9=0的根的情况是( )
A.有一个实数根 B.有两个相等的实数根
C.无实数根 D.有两个不相等的实数根
4.用配方法解一元二次方程x2-2x-7=0,方程可变形为( )
A.(x-2)2=11 B.(x+2)2=11
C.(x-1)2=8 D.(x+1)2=8
5.某商品的进价为每件40元,当售价为每件60元时,每星期可卖出200件,现需降价处理,且经市场调查发现:每降价1元,每星期可多卖出8件.若店里每周利润要达到8 450元,设店主把该商品每件售价降低x元,则可列方程为( )
A.(60-x)(200+8x)=8 450 B.(20-x)(200+x)=8 450
C.(20-x)(200+40x)=8 450 D.(20-x)(200+8x)=8 450
6.解方程:
3x2-1=2x+4.
7.已知关于x的一元二次方程x2+2x-k=0有实数根.
(1)求k的取值范围;
(2)若方程有一个根为2,求方程的另一根.
解:(1)由题意,得Δ=b2-4ac=22-4×1×(-k)=4+4k≥0,
解得k≥-1.
8.如图①,某校进行校园改造,准备将一块正方形空地划出部分区域栽种鲜花,原空地一边减少了4 m,另一边减少了5 m,剩余部分的面积为650 m2.
(1)求原正方形空地的边长;
(2)在实际建造时,从校园美观和实用的角度考虑,按图②的方式进行改造,先在正方形空地一侧建成1 m宽的画廊,再在余下地方建成宽度相等的两条小道后,其余地方栽种鲜花,如果栽种鲜花区域的面积为812 m2,求小道的宽度.
解
一元二次方程
1.下列方程属于一元二次方程的是( )
A.x3+x2+2=0 B.y=5-x
C.x+=5 D.x2+2x=3
2.把方程x2-3(x+1)=2x化成一般形式正确的是( )
A.x2-x-3=0 B.x2+x+3=0
C.x2-5x-3=0 D.x2-5x+3=0
3.将方程x2-2=7x化成x2+bx+c=0的形式,则一次项是 -7x,b+c=-9.
4.若关于x的一元二次方程(m-2)x2-x+m2-4=0的常数项为0,则m的值为-2.
5.一个直角三角形的两条直角边相差3 cm,面积是9 cm2,设较长的直角边的长为x cm,根据题意,可列方程为 x(x-3)=9.
6.若已知两个数的积为12,和为7,设其中一个数为x,则依题意可列方程x(7-x)=12.
7.设a是二次项系数,b是一次项系数,c是常数项,且满足(a-3)2++=0,求满足条件的一元二次方程.
一元二次方程的解
1.已知x=2是方程x2-2x+c=0的一个根,则实数c的值是( )
A.-1 B.0
C.1 D.2
2.写出有一个根为x=1的一元二次方程,它可以是x2-1=0(答案不唯一).
3.根据下表确定一元二次方程x2+2x-9=0的一个解的范围是2<x<3.
x 0 1 2 3 4
x2+2x-9 -9 -6 -1 6 15
4.根据下列表格的对应值:
x 2.4 2.5 2.6 2.7
ax2+bx+c(近似值) 5.6 5.7 5.8 5.9
判断方程ax2+bx+c=5.78(a≠0,a,b,c为常数)的一个近似解是( )
A.2.41 B.2.57
C.2.63 D.2.67
5.在一元二次方程ax2+bx+c=0中,若a,b,c满足关系式a-b+c=0,则这个方程必有一个根为x=-1.
6.已知x=-1是方程x2+ax-b=0的一个根,求a2-b2+2b的值.
7.将方程4x2+8x=25化成ax2+bx+c=0的形式,则a,b,c的值分别为( )
A.4,8,25 B.4,-8,-25
C.4,8,-25 D.4,-8,25
解一元二次方程(直接开方法)
1.一元二次方程x2=4的根为( )
A.x1=x2=2 B.x1=x2=-2
C.x1=2,x2=-2 D.x1=4,x2=-4
2.若关于x的方程4x2=m有实数根,则m的取值范围是( )
A.m>0 B.m≥0
C.m<0 D.m≤0
3.方程(x-2)2+4=0的解是( )
A.x1=x2=0 B.x1=2,x2=-2
C.x1=0,x2=4 D.没有实数根
4.一元二次方程3x2-75=0的解为x1=5,x2=-5.
5.解方程:
(1)(x+1)2-25=0;
(2)(2x-5)2=9.
6.若一元二次方程ax2+bx+1=0的一根为x=3,则3a+b的值为- .
解一元二次方程(配方法)
1.用配方法解一元二次方程x2+3x=1时,应在等式两边都加上 .
2.一元二次方程x2-6x+5=0配方后可变形为( )
A.(x-3)2=14 B.(x-3)2=4
C.(x+3)2=14 D.(x+3)2=4
3.用配方法解一元二次方程2x2-3x-1=0,配方正确的是( )
A.(x-)2= B.(x-)2=
C.(x-)2= D.(x-)2=
4.用配方法将方程x2-2x-3=0化成(x-a)2=b的形式,则a+b=5.
5.解方程:
(1)x2+4x-2=0; (2)3x2-6x+1=0.
6.解方程:2(x-1)2-50=0.
解一元二次方程(公式法)
1.用公式法解方程x2+x=2时,求根公式中的a,b,c的值分别是( )
A.a=1,b=1,c=2 B.a=1,b=-1,c=-2
C.a=1,b=1,c=-2 D.a=1,b=-1,c=2
2.用公式法解方程4x2-12x=3时,Δ的值是( )
A.-8 B.8
C.-192 D.192
3.用公式法解方程:2x2-x-1=0.
4.有一个数值转换机,其流程如图所示,若输入的a=-2,则输出的x的值为1或2.
5.解方程:x2+2x-4=0.
解一元二次方程(因式分解法)
1.方程x2-6x=0的解是( )
A.x=6 B.x=0
C.x1=6,x2=0 D.x1=-6,x2=0
2.若x(x-2)=x-2,则x的值为A
A.1或2 B.-1或-2
C.1或-1 D.2或-2
3.一个三角形的两边长为3和8,第三边的长是方程x(x-9)-13(x-9)=0的根,则这个三角形的周长是20.
4.解方程:
(1)3x2-12x=0; (2)x(x-1)=2(1-x).
5.解方程:x2+2=2x.
一元二次方程根的判别式
1.一元二次方程x2+2x-3=0根的判别式的值是16.
2.方程2x2+3x+1=0的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
3.(2022 丹东)关于x的一元二次方程x2+3x+m=0没有实数根,则m的取值范围是 m> .
4.(2022 西藏)已知关于x的一元二次方程(m-1)x2+2x-3=0有实数根,则m的取值范围是( )
A.m≥ B.m<
C.m>且m≠1 D.m≥且m≠1
5.若关于x的一元二次方程(m-1)x2-2(m-1)x+1=0有两个相等的实数根,则m的值是( )
A.0 B.1
C.2 D.1或2
6.解方程:
(1)x2+4x-21=0; (2)x(x-5)=2x-10.
一元二次方程的根与系数的关系
1.一元二次方程x2-5x+4=0的两根之和为( )
A.-5 B.5
C.-4 D.4
2.若一元二次方程x2-5x-7=0有两实数根x1和x2,则下列选项正确的是( )
A.x1+x2=-5 B.x1x2=7
C.x1=x2 D.x1x2-x1-x2=-12
3.已知x1,x2是关于x的方程x2+ax-2b=0的两实数根,且x1+x2=-2,x1 x2=1,则ba的值是A
A. B.-
C.4 D.-1
4.已知x=3是关于x的一元二次方程x2-2x-m=0的根,则该方程的另一个根是-1.
5.已知m,n是一元二次方程x2+4x-2=0的两根,则代数式(m+1)(n+1)的值等于-5.
6.已知关于x的一元二次方程x2-4x+k-1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x+x=10,求k的值.
实际问题与一元二次方程(1)——面积问题
1.用一块长80 cm,宽60 cm的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为1 500 cm2的无盖长方体纸盒,设截去的小正方形的边长为x cm,则可列方程为(80-2x)(60-2x)=1 500.
2.如图所示,把四个长和宽分别为x+2和x的矩形拼接成大正方形.若四个矩形和中间小正方形的面积和为4×35+22,则根据题意能列出的方程是A
A.x2+2x-35=0 B.x2+2x+35=0
C.x2+2x-4=0 D.x2+2x+4=0
第2题图
第3题图
3.如图,幼儿园某教室矩形地面的长为8 m,宽为5 m,现准备在地面正中间铺设一块面积为18 m2的地毯,四周未铺地毯的条形区域的宽度都相同,求四周未铺地毯的条形区域的宽度.
4.等腰三角形的底边长为7,腰长是方程x2-9x+18=0的一个根,则这个等腰三角形的周长为19.
实际问题与一元二次方程(2)——面积问题
1.如图,幼儿园计划用30 m的围栏靠墙围成一个面积为100 m2的矩形小花园(墙长为15 m),则与墙垂直的边x为( )
A.10 m或5 m B.5 m或8 m
C.10 m D.5 m
2.如图所示,某建筑工地要靠一堵院墙围建一个面积为150 m2的矩形临时仓库.已知可利用的院墙长18 m,要求在与院墙平行的一边开一个宽为2 m的门,现有的砖料按要求只能砌成33 m长的围墙,求这个待建临时仓库的长和宽.
3.设a,b是方程x2+x-2 023=0的两个实数根,则ab+a+b的值是-2 024.
实际问题与一元二次方程(3)——增长率问题
1.某旅游景点10月份共接待游客64万人次,12月份共接待游客25万人次,设每月游客人数的平均下降率为x,则下列方程正确的是( )
A.25(1+x)2=64 B.25(1+x2)=64
C.64(1-x)2=25 D.64(1-x2)=25
2.有种传染病蔓延极快,现有一人患有此病,两天后共有144人患病,则平均每天一人传染的人数为( )
A.9 B.10
C.11 D.12
3.某公司2020年盈利1 500万元,到2022年盈利2 160万元,假设每年盈利的年增长率相同.
(1)求该公司每年盈利的年增长率;
(2)若该公司每年盈利的年增长率不变,预计2023年盈利多少万元?
4.若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为24.
实际问题与一元二次方程(4)——互赠、握手问题
1.某生物兴趣小组的同学,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了72件,如果全组有x名同学,则根据题意列出方程是x(x-1)=72.
2.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了21条航线,则这个航空公司共有飞机场( )
A.4个 B.5个
C.6个 D.7个
3.某市体育局要组织一次篮球赛,赛制为单循环形式(每两队之间都赛一场),计划安排28场比赛,应邀请多少支球队参加比赛?
4.某电影因质量很高受到全国观众的喜爱,上映第一天票房约3亿元,以后每天票房按相同的增长率增长,三天后票房收入累计达10亿元,若把增长率记作x,则方程可以列为( )
A.3(1+x)=10
B.3(1+x)2=10
C.3+3(1+x)2=10
D.3+3(1+x)+3(1+x)2=10
实际问题与一元二次方程(5)——营销问题
1.某戏院举办文艺演出,经调研,当票价每张30元时,1 200张门票可以全部售出.票价每增加1元,售出的门票就减少20张,若涨价后,门票总收入达到38 500元,设票价每张x元,则可列方程为( )
A.x(1 200-20x)=38 500
B.x=38 500
C.(x-30)(1 200-20x)=38 500
D.(x-30)=38 500
2.在商场中,某运动品牌的鞋子,每天可销售20双,每双可获利40元.为庆祝新年,对该鞋子进行促销活动,该鞋子每双降价1元,平均每天可多售出2双.若设该鞋子每双每降价x元,请解答下列问题:
(1)用含x的代数式表示:降价x元后,每售出一双该鞋子可获得利润(40-x)元,平均每天可售出(20+2x)双该鞋子;
(2)在此次促销活动中,每双鞋子降价多少元,可使该品牌的鞋子每天盈利1 250元?
3.若一元二次方程x2-2x+a=0有一根为-1,则另一根为( )
A.5 B.-3
C.4 D.3
第二章复习
1.将一元二次方程2x2-1=x化成一般形式后,二次项系数和一次项系数分别是( )
A.-2,-1 B.2,0
C.2,1 D.2,-1
2.若x1,x2是一元二次方程x2-3x-2=0的两个根,则x1x2的值是( )
A.3 B.-2
C.-3 D.2
3.方程x2-x+9=0的根的情况是( )
A.有一个实数根 B.有两个相等的实数根
C.无实数根 D.有两个不相等的实数根
4.用配方法解一元二次方程x2-2x-7=0,方程可变形为( )
A.(x-2)2=11 B.(x+2)2=11
C.(x-1)2=8 D.(x+1)2=8
5.某商品的进价为每件40元,当售价为每件60元时,每星期可卖出200件,现需降价处理,且经市场调查发现:每降价1元,每星期可多卖出8件.若店里每周利润要达到8 450元,设店主把该商品每件售价降低x元,则可列方程为( )
A.(60-x)(200+8x)=8 450 B.(20-x)(200+x)=8 450
C.(20-x)(200+40x)=8 450 D.(20-x)(200+8x)=8 450
6.解方程:
3x2-1=2x+4.
7.已知关于x的一元二次方程x2+2x-k=0有实数根.
(1)求k的取值范围;
(2)若方程有一个根为2,求方程的另一根.
解:(1)由题意,得Δ=b2-4ac=22-4×1×(-k)=4+4k≥0,
解得k≥-1.
8.如图①,某校进行校园改造,准备将一块正方形空地划出部分区域栽种鲜花,原空地一边减少了4 m,另一边减少了5 m,剩余部分的面积为650 m2.
(1)求原正方形空地的边长;
(2)在实际建造时,从校园美观和实用的角度考虑,按图②的方式进行改造,先在正方形空地一侧建成1 m宽的画廊,再在余下地方建成宽度相等的两条小道后,其余地方栽种鲜花,如果栽种鲜花区域的面积为812 m2,求小道的宽度.
解
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
