24.4.2 圆锥的侧面积和全面积 课件(共26张PPT)【2023秋人教九上数学高效实用备课】
文档属性
| 名称 | 24.4.2 圆锥的侧面积和全面积 课件(共26张PPT)【2023秋人教九上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 25.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-07 22:50:17 | ||
图片预览






文档简介
(共26张PPT)
人教九上数学同步精品课件
人教版九年级上册
24.4.2 圆锥的侧面积和全面积
第二十四章 圆
24.4 弧长和扇形的面积
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.体会圆锥侧面积的探索过程,明确对应关系.
2.掌握圆锥的侧面积和全面积公式,并能解决一些简单的实际问题.
学习目标
重点
难点
生活中的圆锥
新课引入
今天我们就来学习有关圆锥的一些知识
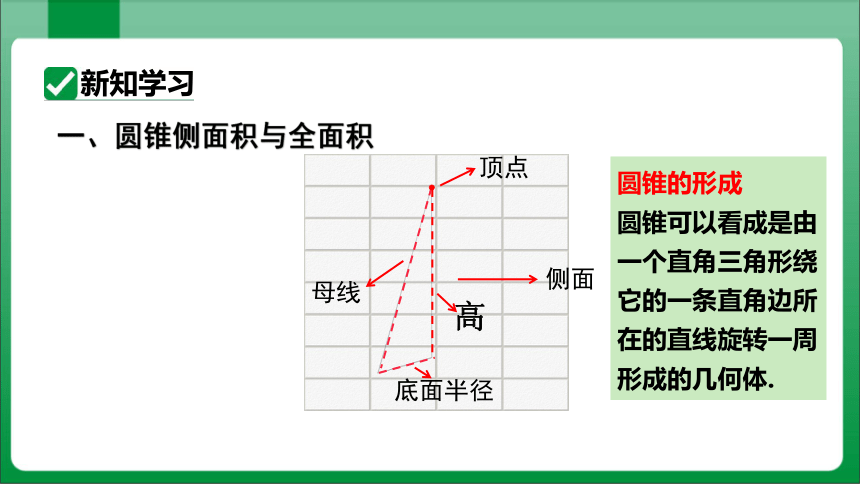
一、圆锥侧面积与全面积
顶点
母线
底面半径
侧面
高
圆锥的形成
圆锥可以看成是由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的几何体.
新知学习
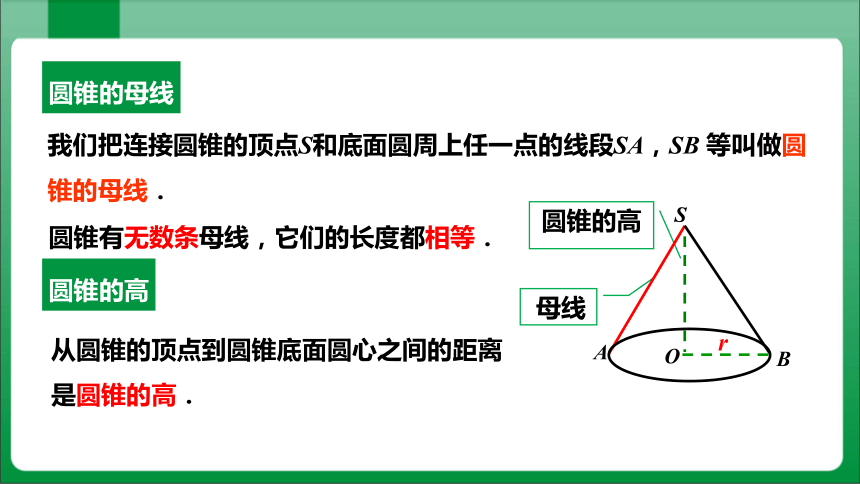
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆周上任一点的线段SA,SB 等叫做圆锥的母线.
圆锥的母线
圆锥有无数条母线,它们的长度都相等.
圆锥的高
从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
h
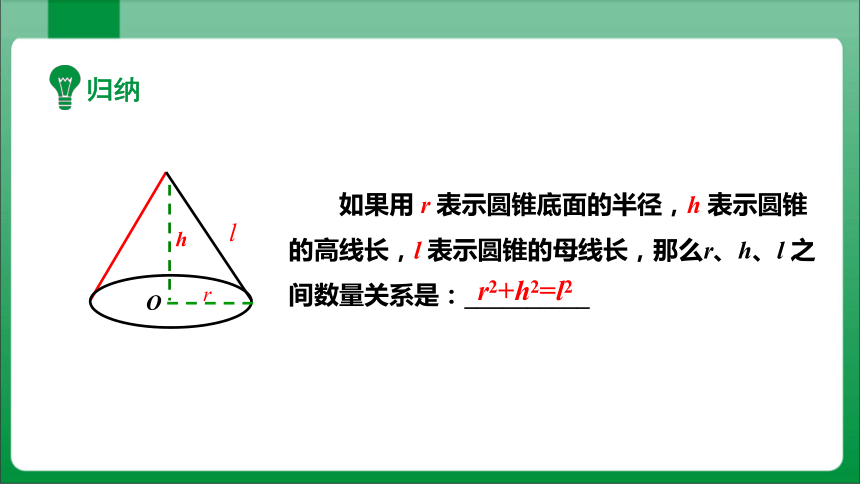
如果用 r 表示圆锥底面的半径,h 表示圆锥的高线长,l 表示圆锥的母线长,那么r、h、l 之间数量关系是:__________
O
r
r2+h2=l2
归纳
思考
问题1 圆锥的侧面展开图是什么图形?
l
o
r
扇形
圆锥的侧面展开图是扇形
问题2 沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题3 圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
相等
母线
请推导出圆锥的侧面积公式.
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积 ( 或表面积 ).
S全 = S侧+S底 = πrl+πr2
针对训练
1.若一个圆锥的侧面展开图是半径为 18 cm,圆心角为 240° 的扇形,则这个圆锥的底面半径是( )
A. 6 cm B. 9 cm C. 12 cm D. 18 cm
C
2. (1)已知圆锥的底面直径为 4,母线长为 6,求它的侧面积.
(2)已知圆锥底面圆的半径为 2 cm ,高为 cm ,这个圆锥的侧面积和全面积.
例1 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建 20个底面积为 12 m2,高为 3.2 m,外围高 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π取3.142,结果取整数 )
二、圆锥面积的应用
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为 12 m2,高 h2=1.8 m;
上部圆锥的高 h1=3.2-1.8=1.4(m).
侧面积为 2π×1.954×1.8≈22.10 (m2).
侧面展开扇形的弧长为 2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建 20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
h1
h2
r
圆柱的底面圆的半径 r =
圆锥的母线长 l =
针对训练
1.圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积( 取3.14,结果保留2个有效数字)
解:∵l=80,h=38.7,
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2).
答:烟囱帽的面积约为1.8×104cm2.
l
h
r
2.如图,已知扇形OAB的半径为6 cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)围成的圆锥的侧面积为多少?
∴圆锥的侧面积 .
解:(1) 由已知得扇形的半径 R = 6cm.
(2) 该圆锥的底面半径是多少?
根据题意得 ,解得 r=2.
解:(2) 该圆锥的底面半径为r cm,
即圆锥的底面半径为 2 cm.
随堂练习
1.如图,已知圆锥的母线长为8,底面圆的半径为2,若一只蚂蚁从A点出发,绕圆锥的侧面爬行一周后又回到A点,则此蚂蚁爬行的最短距离为________.
思路点拨:借助侧面展开找最短路径
2.在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )
A. 12π B. 15π C. 20π D.24π
C
3.(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?
A
B
C
①
②
③
O
解:(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=
(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
A
B
C
①
②
③
O
(2)圆锥侧面展开图的弧长为:
(3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
F
(3)连接AO并延长交⊙O于点F,交扇形于点E, ,
最大半径为 .所以不能.
2. 圆锥的侧面积及全面积公式:S侧=πrl,
S全=S侧+S底= πrl+ πr2=πr(r+l)
圆锥的高
母线
S
A
O
B
r
l
o
r
扇形
1.r、h、l的关系:
r2+h2=l2
3.①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
24.4.2 圆锥的侧面积和全面积
第二十四章 圆
24.4 弧长和扇形的面积
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.体会圆锥侧面积的探索过程,明确对应关系.
2.掌握圆锥的侧面积和全面积公式,并能解决一些简单的实际问题.
学习目标
重点
难点
生活中的圆锥
新课引入
今天我们就来学习有关圆锥的一些知识
一、圆锥侧面积与全面积
顶点
母线
底面半径
侧面
高
圆锥的形成
圆锥可以看成是由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的几何体.
新知学习
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆周上任一点的线段SA,SB 等叫做圆锥的母线.
圆锥的母线
圆锥有无数条母线,它们的长度都相等.
圆锥的高
从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
h
如果用 r 表示圆锥底面的半径,h 表示圆锥的高线长,l 表示圆锥的母线长,那么r、h、l 之间数量关系是:__________
O
r
r2+h2=l2
归纳
思考
问题1 圆锥的侧面展开图是什么图形?
l
o
r
扇形
圆锥的侧面展开图是扇形
问题2 沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题3 圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
相等
母线
请推导出圆锥的侧面积公式.
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积 ( 或表面积 ).
S全 = S侧+S底 = πrl+πr2
针对训练
1.若一个圆锥的侧面展开图是半径为 18 cm,圆心角为 240° 的扇形,则这个圆锥的底面半径是( )
A. 6 cm B. 9 cm C. 12 cm D. 18 cm
C
2. (1)已知圆锥的底面直径为 4,母线长为 6,求它的侧面积.
(2)已知圆锥底面圆的半径为 2 cm ,高为 cm ,这个圆锥的侧面积和全面积.
例1 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建 20个底面积为 12 m2,高为 3.2 m,外围高 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π取3.142,结果取整数 )
二、圆锥面积的应用
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为 12 m2,高 h2=1.8 m;
上部圆锥的高 h1=3.2-1.8=1.4(m).
侧面积为 2π×1.954×1.8≈22.10 (m2).
侧面展开扇形的弧长为 2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建 20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
h1
h2
r
圆柱的底面圆的半径 r =
圆锥的母线长 l =
针对训练
1.圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积( 取3.14,结果保留2个有效数字)
解:∵l=80,h=38.7,
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2).
答:烟囱帽的面积约为1.8×104cm2.
l
h
r
2.如图,已知扇形OAB的半径为6 cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)围成的圆锥的侧面积为多少?
∴圆锥的侧面积 .
解:(1) 由已知得扇形的半径 R = 6cm.
(2) 该圆锥的底面半径是多少?
根据题意得 ,解得 r=2.
解:(2) 该圆锥的底面半径为r cm,
即圆锥的底面半径为 2 cm.
随堂练习
1.如图,已知圆锥的母线长为8,底面圆的半径为2,若一只蚂蚁从A点出发,绕圆锥的侧面爬行一周后又回到A点,则此蚂蚁爬行的最短距离为________.
思路点拨:借助侧面展开找最短路径
2.在Rt△ABC中,∠C=90°,AC=3,BC=4,以AC所在直线为轴,把△ABC旋转1周,得到圆锥,则该圆锥的侧面积为( )
A. 12π B. 15π C. 20π D.24π
C
3.(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?
A
B
C
①
②
③
O
解:(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=
(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
A
B
C
①
②
③
O
(2)圆锥侧面展开图的弧长为:
(3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
F
(3)连接AO并延长交⊙O于点F,交扇形于点E, ,
最大半径为 .所以不能.
2. 圆锥的侧面积及全面积公式:S侧=πrl,
S全=S侧+S底= πrl+ πr2=πr(r+l)
圆锥的高
母线
S
A
O
B
r
l
o
r
扇形
1.r、h、l的关系:
r2+h2=l2
3.①其侧面展开图扇形的半径=母线的长l
②侧面展开图扇形的弧长=底面周长
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
