分类加法计数原理与分布乘法计数原理3
文档属性
| 名称 | 分类加法计数原理与分布乘法计数原理3 |

|
|
| 格式 | rar | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-28 00:00:00 | ||
图片预览






文档简介
课件14张PPT。分类计数原理与
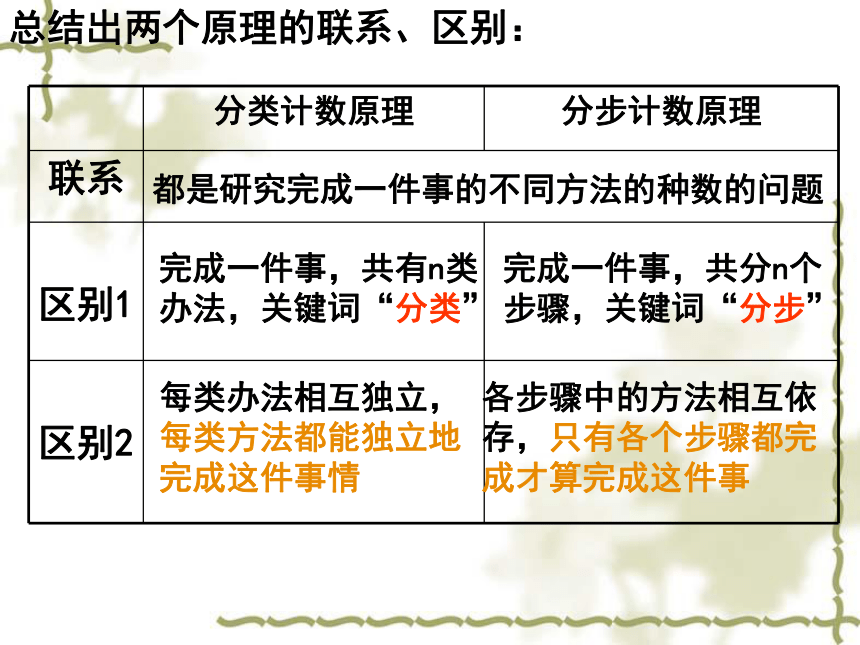
分步计数原理(3)一、分类计数原理 完成一件事, 有 n 类办法, 在第 1 类办法中有 m1 种不同的方法, 在第 2 类办法中有 m2 种不同的方法……在第 n 类办法中有 mn 种不同的方法. 那么完成这件事共有 N=m1+m2+…+mn种不同的方法. 二、分步计数原理 完成一件事, 需要分成 n 个步骤, 做第 1 步有 m1 种不同的方法, 做第 2 步有 m2 种不同的方法……做第 n 步有 mn 种不同的方法. 那么完成这件事共有 N=m1×m2×…×mn种不同的方法. 三、共同点把一个原始事件分解成若干个分事件来完成.四、区别一个和分类有关, 一个与分步有关. 回顾总结出两个原理的联系、区别:完成一件事,共有n类办法,关键词“分类”完成一件事,共分n个步骤,关键词“分步”每类办法相互独立,每类方法都能独立地完成这件事情各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事都是研究完成一件事的不同方法的种数的问题 例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个?
分析与解:分析个位数字,可分以下几类.
个位是9,则十位可以是1,2,3…,8中的一个,故有8个;
个位是8,则十位可以是1,2,3…,7中的一个,故有7个;
与上同样:
个位是7的有6个;
个位是6的有5个;
……
个位是2的只有1个.
由分类计数原理知,满足条件的两位数有说明:本题是用分类计数原理解答的,结合本题可加深对“做一件事,完成之可以有n类办法”的理解,所谓“做一件事,完成它可以有n类办法”,这里是指对完成这件事情的所有办法的一个分类.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次分类时要注意满足一个基本要求:完成这件事的任何一种方法必须属于某一类,并且分别属于不同两类的两种方法是不同的方法,只有满足这些条件,才可以用分类计数原理. 综合应用例2:为了确保电子信箱的安全,在注册时,通常要设置电子信箱密码,在某网站设置的信箱中
(1)密码为4位,每位均为0到9这10个数字中的一个,这样的密码共有多少个?
(2)密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
(3)密码为4-6位,每位均为0到9这10个数字中的一个,这样的密码共有多少个?
变:若问从0到9共10个数字可以组成多少个四位数? 综合应用1.有不同的中文书9本,不同的英文书7本,不同的日文书5本.从其中取出不是同一国文字的书2本,问有多少种不同的取法?
2.集合A={1,2,-3},B={-1,-2,3,4} .从A,B 中各取1个元素作为点P(x,y) 的坐标.
(1)可以得到多少个不同的点?
(2)这些点中,位于第一象限的有几个?
(3)这些点中,有多少个不落在直线y=-x上?
练习9×7+9×5+7×5=1433×4+4×3=242×2+2×2=824-6=18例4.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?解:由题意可知,在艺术组9人中,有且仅有一人既会钢琴又会小号(把该人称为“多面手”),只会钢琴的有6人,只会小号的有2人,把会钢琴、小号各1人的选法分为两类:
第一类:多面手入选,另一人只需从其他8人中任选一个,故这类选法共有8种.
第二类:多面手不入选,则会钢琴者只能从6个只会钢琴的人中选出,会小号的1人也只能从只会小号的 2人中选出,放这类选法共有6×2=12种,
故共有20种不同的选法.例5.现要安排一份5天值班表,每天有一个人值班。共有5个人,每个人都可以值多天班或不值班,但相邻两天不能由同一个人值班,问此值班表由多少种不同的排法?解:分5步进行:
第一步:先排第一天,可排5人中的任一个,有5种排法;
第二步:再排第二天,此时不能排第一天的人,有4种排法;
第三步:再排第三天,此时不能排第二天的人,有4种排法;
第四步:同前
第五步:同前
由分步计数原理可得不同排法有5×4×4×4×4=1280种例6. ①用0,1,2,……,9可以组成多少个8位号码;
②用0,1,2,……,9可以组成多少个8位整数;
③用0,1,2,……,9可以组成多少个无重复数字的4位整数;
④用0,1,2,……,9可以组成多少个有重复数字的4位整数;
⑤用0,1,2,……,9可以组成多少个无重复数字的4位奇数;10×10×10×10×10×10×10×10=1089×10×10×10×10×10×10×10=9×1079×9×8×7=45369×10×10×10=9000先定个位,再定千位,最后定百、十位5×8×8×7=2240例 8. 5张1元币,4张1角币,1张5分币,2张2分币,
可组成多少种不同的币值?(1张不取,即0元0分0角不计在内)元:0,1,2,3,4,5
角:0,1,2,3,4
分:0,2,4,5,7,9
6×5×6-1=179例9.自然数2520有多少个约数?解:2520=23×32×5×7
分四步完成:
第一步:取20,21,22,23,24有4种;
第二步:取30,31,32有3种;
第三步:取50,51有2种;
第四步:取70,71有2种。
由分步计数原理,共有4×3×2×2=48种小 结两个原理的选择 如果完成一件事情有 n 类办法, 这 n 类办法彼此之间是相互独立的, 无论哪一类办法中的哪一种方法都能单独完成这件事情, 求完成这件事情的方法种数, 就用分类计数原理.关于分类 首先要根据问题的特点确定一个分类的标准, 然后再分类;其次分类时要掌握两个原则:(1)完成这件事的任何一种方法都必须属于某一类;
(2)分别属于不同两类的方法是不同的方法.不重不漏(1)确定分步标准; (2)分成的 n 个步骤要连续完成; (3)每步中任何一种方法都可以与下一步中的任何一种方 法连接.注:既可分类又需分步时, 一般先分类后分步.关于分步 如果完成一件事情需要分成 n 个步骤, 各个步骤都是不可缺少的, 需要依次完成所有的步骤, 才能完成这件事情, 而完成每一个步骤各有若干种不同的方法, 求完成这件事情的方法种数就用分步计数原理.
分步计数原理(3)一、分类计数原理 完成一件事, 有 n 类办法, 在第 1 类办法中有 m1 种不同的方法, 在第 2 类办法中有 m2 种不同的方法……在第 n 类办法中有 mn 种不同的方法. 那么完成这件事共有 N=m1+m2+…+mn种不同的方法. 二、分步计数原理 完成一件事, 需要分成 n 个步骤, 做第 1 步有 m1 种不同的方法, 做第 2 步有 m2 种不同的方法……做第 n 步有 mn 种不同的方法. 那么完成这件事共有 N=m1×m2×…×mn种不同的方法. 三、共同点把一个原始事件分解成若干个分事件来完成.四、区别一个和分类有关, 一个与分步有关. 回顾总结出两个原理的联系、区别:完成一件事,共有n类办法,关键词“分类”完成一件事,共分n个步骤,关键词“分步”每类办法相互独立,每类方法都能独立地完成这件事情各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事都是研究完成一件事的不同方法的种数的问题 例1 在所有的两位数中,个位数字比十位数字大的两位数有多少个?
分析与解:分析个位数字,可分以下几类.
个位是9,则十位可以是1,2,3…,8中的一个,故有8个;
个位是8,则十位可以是1,2,3…,7中的一个,故有7个;
与上同样:
个位是7的有6个;
个位是6的有5个;
……
个位是2的只有1个.
由分类计数原理知,满足条件的两位数有说明:本题是用分类计数原理解答的,结合本题可加深对“做一件事,完成之可以有n类办法”的理解,所谓“做一件事,完成它可以有n类办法”,这里是指对完成这件事情的所有办法的一个分类.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次分类时要注意满足一个基本要求:完成这件事的任何一种方法必须属于某一类,并且分别属于不同两类的两种方法是不同的方法,只有满足这些条件,才可以用分类计数原理. 综合应用例2:为了确保电子信箱的安全,在注册时,通常要设置电子信箱密码,在某网站设置的信箱中
(1)密码为4位,每位均为0到9这10个数字中的一个,这样的密码共有多少个?
(2)密码为4位,每位是0到9这10个数字中的一个,或是从A到Z这26个英文字母中的1个,这样的密码共有多少个?
(3)密码为4-6位,每位均为0到9这10个数字中的一个,这样的密码共有多少个?
变:若问从0到9共10个数字可以组成多少个四位数? 综合应用1.有不同的中文书9本,不同的英文书7本,不同的日文书5本.从其中取出不是同一国文字的书2本,问有多少种不同的取法?
2.集合A={1,2,-3},B={-1,-2,3,4} .从A,B 中各取1个元素作为点P(x,y) 的坐标.
(1)可以得到多少个不同的点?
(2)这些点中,位于第一象限的有几个?
(3)这些点中,有多少个不落在直线y=-x上?
练习9×7+9×5+7×5=1433×4+4×3=242×2+2×2=824-6=18例4.某艺术组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?解:由题意可知,在艺术组9人中,有且仅有一人既会钢琴又会小号(把该人称为“多面手”),只会钢琴的有6人,只会小号的有2人,把会钢琴、小号各1人的选法分为两类:
第一类:多面手入选,另一人只需从其他8人中任选一个,故这类选法共有8种.
第二类:多面手不入选,则会钢琴者只能从6个只会钢琴的人中选出,会小号的1人也只能从只会小号的 2人中选出,放这类选法共有6×2=12种,
故共有20种不同的选法.例5.现要安排一份5天值班表,每天有一个人值班。共有5个人,每个人都可以值多天班或不值班,但相邻两天不能由同一个人值班,问此值班表由多少种不同的排法?解:分5步进行:
第一步:先排第一天,可排5人中的任一个,有5种排法;
第二步:再排第二天,此时不能排第一天的人,有4种排法;
第三步:再排第三天,此时不能排第二天的人,有4种排法;
第四步:同前
第五步:同前
由分步计数原理可得不同排法有5×4×4×4×4=1280种例6. ①用0,1,2,……,9可以组成多少个8位号码;
②用0,1,2,……,9可以组成多少个8位整数;
③用0,1,2,……,9可以组成多少个无重复数字的4位整数;
④用0,1,2,……,9可以组成多少个有重复数字的4位整数;
⑤用0,1,2,……,9可以组成多少个无重复数字的4位奇数;10×10×10×10×10×10×10×10=1089×10×10×10×10×10×10×10=9×1079×9×8×7=45369×10×10×10=9000先定个位,再定千位,最后定百、十位5×8×8×7=2240例 8. 5张1元币,4张1角币,1张5分币,2张2分币,
可组成多少种不同的币值?(1张不取,即0元0分0角不计在内)元:0,1,2,3,4,5
角:0,1,2,3,4
分:0,2,4,5,7,9
6×5×6-1=179例9.自然数2520有多少个约数?解:2520=23×32×5×7
分四步完成:
第一步:取20,21,22,23,24有4种;
第二步:取30,31,32有3种;
第三步:取50,51有2种;
第四步:取70,71有2种。
由分步计数原理,共有4×3×2×2=48种小 结两个原理的选择 如果完成一件事情有 n 类办法, 这 n 类办法彼此之间是相互独立的, 无论哪一类办法中的哪一种方法都能单独完成这件事情, 求完成这件事情的方法种数, 就用分类计数原理.关于分类 首先要根据问题的特点确定一个分类的标准, 然后再分类;其次分类时要掌握两个原则:(1)完成这件事的任何一种方法都必须属于某一类;
(2)分别属于不同两类的方法是不同的方法.不重不漏(1)确定分步标准; (2)分成的 n 个步骤要连续完成; (3)每步中任何一种方法都可以与下一步中的任何一种方 法连接.注:既可分类又需分步时, 一般先分类后分步.关于分步 如果完成一件事情需要分成 n 个步骤, 各个步骤都是不可缺少的, 需要依次完成所有的步骤, 才能完成这件事情, 而完成每一个步骤各有若干种不同的方法, 求完成这件事情的方法种数就用分步计数原理.
