12.2.3 多项式与多项式相乘课件(共16张PPT) 2023—2024学年华东师大版数学八年级上册
文档属性
| 名称 | 12.2.3 多项式与多项式相乘课件(共16张PPT) 2023—2024学年华东师大版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 13:26:08 | ||
图片预览






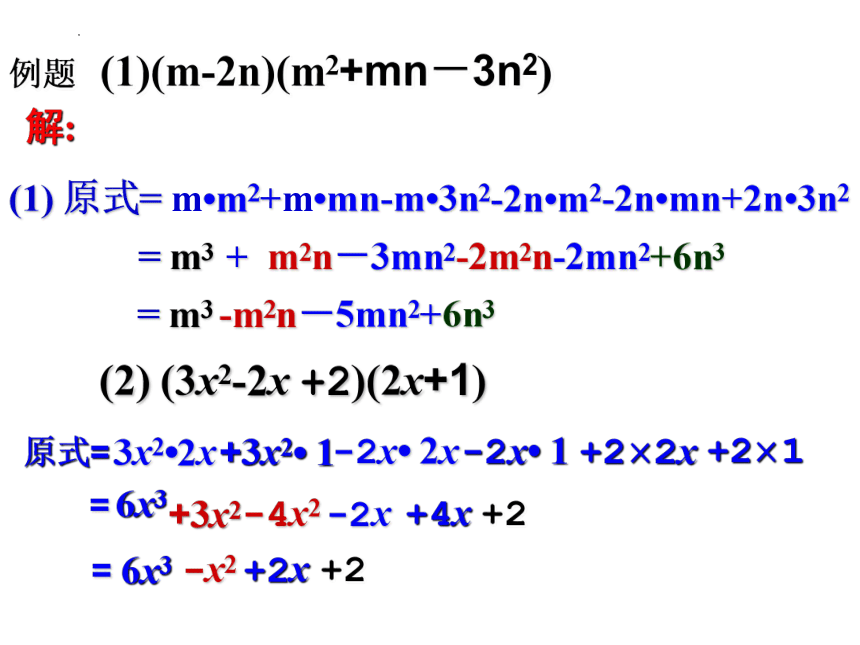
文档简介
(共16张PPT)
第12章 整式的乘除
12.2 整式的乘法
29中二年级数学课件
华东师大版八年级数学(上)
3、多项式与多项式相乘
回顾与思考
回顾 & 思考
② 再把所得的积相加
如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的每一项
进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.(同正、异负)
某地区在退耕还林期间,有一块原长为m米,宽
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。
a
m
b
n
自 探 一:
ma
mb
na
nb
a+b
m+n
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
你能运用所学的知识说明此等式成立的道理吗?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb
(m+n)(a+b)
= (m+n)a+(m+n)b
(m+n)(a+b)
1
2
3
4
=
ma
1
2
3
4
+mb
+na
+nb
多项式乘以多项式的法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
合 探 一 :
例题解析
运 用 一:
例: 计算:(1)(x+2)(x 3) (2)(3x -1)(2x+1)
解:
(1) (x+2)(x 3)
3x
+ 2x
=
x2 - x - 6
-2×3
(2) (3x -1)(2x+1)
=
= x﹒x
3x 2x
+3x 1
-1 2 x
1
=
6x2
+ 3x
-2 x
1
=
6x2 + x 1
所得积的符号由这
两项的符号来确定:
同 号 得正
异 号 得负
注意
两项相乘时,先定符号。
最后的结果要合并同类项.
例题 (1)(m-2n)(m2+mn-3n2)
解:
(1) 原式= m m2+m mn-m 3n2-2n m2-2n mn+2n 3n2
(2) (3x2-2x +2)(2x+1)
原式=
3x2 2x
+3x2 1
-2x 2x
= m3 + m2n-3mn2-2m2n-2mn2+6n3
= m3 -m2n-5mn2+6n3
-2x 1
+2×2x
+2×1
=
6x3
+3x2
-4x2
-2x
+4x
+2
=
6x3
-x2
+2x
+2
运 用 二:
练习计算:(1)(x 3y)(x+7y) (2)(2x + 5y)(3x 2y)
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
-
=
x2 + 4xy - 21y2
21y2
(2) (2x +5 y)(3x 2y)
=
= x2
2x 3x
2x 2y
+5 y 3x
5y 2y
=
6x2
4xy
+ 15xy
10y2
=
6x2 +11xy 10y2
注意:
1、必须做到不重复,不遗漏.
2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}.
思考:
多项式乘以多项式时需要注意的问题有哪些?
随堂练习
拓展运用
计算:
(1)
(2)
(3)
(4m+5n)(4m-5n)
(a-3b)(a-3b)
化简得:16m2-25n2
化简得:a2-6ab+9b2
化简得:x3-y3
方法与规律
延伸训练:
活动& 探索
填空:
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
56
1 (-6)
(-1) (-6)
(-5) 6
口答:
(-2)
(-35)
解方程:若(2x+3)(2x–1)=x(4x+1)+3
提高训练
如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。
解:(x2+bx+8)(x2 – 3x+c)
原式=x4–3x3+c x2+bx3–3bx2+bcx+8x2–24x+8c
=x4+(b–3)x3+(c–3b+8)x2+(bc–24)x+8c
x2项系数为:c –3b+8
x3项系数为:b – 3
= 0
= 0
∴ b=3 , c=1
若(x–1)(x2 +ax+b)=x3-6x2+11x-6求a、b的值。
提高训练
(x2+mx+n)(x2-3x+2)不含x3,x2项求m,n
先化简(x-4)(x – 2)-(x-1)(x + 3)再求当x=5/2时代数式的值。
解:(x-4)(x – 2)–(x-1)(x +3)
=x2–6x+8–(x2+2x–3)
=x2–6x+8–x2–2x+3
= – 8x+11
当x= – 时
1
2
原式= – 8×( ) +11
1
2
=-9
先化简再求值(2x-5)(3x+2)–6(x+1)(x-2),
求中x=
1
5
提高训练
小 结
多项式乘以多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
注意:
1、必须做到不重复,不遗漏.
2、注意确定积中每一项的符号.
3、结果应化为最简式。
祝学习进步
作业
1.课本P29练习题1,2题
2.课本P30习题12.2第5,6题。
3.跟踪练习册12.2(3)
4.同步作业集:P23-24页 3多项式乘以多项式
学习这件事有人教你很好但最重要的是在于你自己有没有觉悟和恒心。
第12章 整式的乘除
12.2 整式的乘法
29中二年级数学课件
华东师大版八年级数学(上)
3、多项式与多项式相乘
回顾与思考
回顾 & 思考
② 再把所得的积相加
如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的每一项
进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项
② 去括号时注意符号的确定.(同正、异负)
某地区在退耕还林期间,有一块原长为m米,宽
为a米的长方形林区增长了n米,加宽了b米,
请你表示这块林区现在的面积。
a
m
b
n
自 探 一:
ma
mb
na
nb
a+b
m+n
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
你能运用所学的知识说明此等式成立的道理吗?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb
(m+n)(a+b)
= (m+n)a+(m+n)b
(m+n)(a+b)
1
2
3
4
=
ma
1
2
3
4
+mb
+na
+nb
多项式乘以多项式的法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
合 探 一 :
例题解析
运 用 一:
例: 计算:(1)(x+2)(x 3) (2)(3x -1)(2x+1)
解:
(1) (x+2)(x 3)
3x
+ 2x
=
x2 - x - 6
-2×3
(2) (3x -1)(2x+1)
=
= x﹒x
3x 2x
+3x 1
-1 2 x
1
=
6x2
+ 3x
-2 x
1
=
6x2 + x 1
所得积的符号由这
两项的符号来确定:
同 号 得正
异 号 得负
注意
两项相乘时,先定符号。
最后的结果要合并同类项.
例题 (1)(m-2n)(m2+mn-3n2)
解:
(1) 原式= m m2+m mn-m 3n2-2n m2-2n mn+2n 3n2
(2) (3x2-2x +2)(2x+1)
原式=
3x2 2x
+3x2 1
-2x 2x
= m3 + m2n-3mn2-2m2n-2mn2+6n3
= m3 -m2n-5mn2+6n3
-2x 1
+2×2x
+2×1
=
6x3
+3x2
-4x2
-2x
+4x
+2
=
6x3
-x2
+2x
+2
运 用 二:
练习计算:(1)(x 3y)(x+7y) (2)(2x + 5y)(3x 2y)
解:
(1) (x 3y)(x+7y)
+
7xy
3yx
-
=
x2 + 4xy - 21y2
21y2
(2) (2x +5 y)(3x 2y)
=
= x2
2x 3x
2x 2y
+5 y 3x
5y 2y
=
6x2
4xy
+ 15xy
10y2
=
6x2 +11xy 10y2
注意:
1、必须做到不重复,不遗漏.
2、注意确定积中每一项的符号.
3、结果应化为最简式
{合并同类项}.
思考:
多项式乘以多项式时需要注意的问题有哪些?
随堂练习
拓展运用
计算:
(1)
(2)
(3)
(4m+5n)(4m-5n)
(a-3b)(a-3b)
化简得:16m2-25n2
化简得:a2-6ab+9b2
化简得:x3-y3
方法与规律
延伸训练:
活动& 探索
填空:
观察上面四个等式,你能发现什么规律?
你能根据这个规律解决下面的问题吗?
56
1 (-6)
(-1) (-6)
(-5) 6
口答:
(-2)
(-35)
解方程:若(2x+3)(2x–1)=x(4x+1)+3
提高训练
如果(x2+bx+8)(x2 – 3x+c)的乘积中不含x2和x3的项,求b、c的值。
解:(x2+bx+8)(x2 – 3x+c)
原式=x4–3x3+c x2+bx3–3bx2+bcx+8x2–24x+8c
=x4+(b–3)x3+(c–3b+8)x2+(bc–24)x+8c
x2项系数为:c –3b+8
x3项系数为:b – 3
= 0
= 0
∴ b=3 , c=1
若(x–1)(x2 +ax+b)=x3-6x2+11x-6求a、b的值。
提高训练
(x2+mx+n)(x2-3x+2)不含x3,x2项求m,n
先化简(x-4)(x – 2)-(x-1)(x + 3)再求当x=5/2时代数式的值。
解:(x-4)(x – 2)–(x-1)(x +3)
=x2–6x+8–(x2+2x–3)
=x2–6x+8–x2–2x+3
= – 8x+11
当x= – 时
1
2
原式= – 8×( ) +11
1
2
=-9
先化简再求值(2x-5)(3x+2)–6(x+1)(x-2),
求中x=
1
5
提高训练
小 结
多项式乘以多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
注意:
1、必须做到不重复,不遗漏.
2、注意确定积中每一项的符号.
3、结果应化为最简式。
祝学习进步
作业
1.课本P29练习题1,2题
2.课本P30习题12.2第5,6题。
3.跟踪练习册12.2(3)
4.同步作业集:P23-24页 3多项式乘以多项式
学习这件事有人教你很好但最重要的是在于你自己有没有觉悟和恒心。
