去括号(广东省揭阳市揭东县)
图片预览

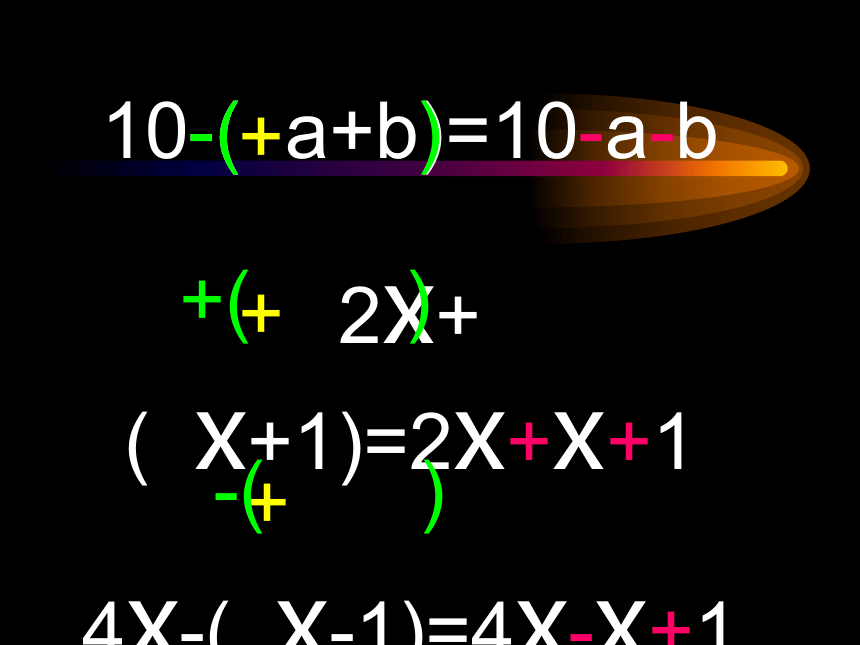


文档简介
(共16张PPT)
引入新课
问题1:小聪带了10元钱去商店购物,花了a元买文具盒,b元买铅笔,他剩下的钱可以用代数式表示为_____________
10-(a+b)
10-a-b
10-(a+b)
10-a-b
=
新
课
情景1:如图,
要
搭x个正方形,需
要多少根火柴棒?
……
可用代数式表示为:
4x-(x-1),2x+(x+1),3x+1
x个
(1)上述几个代数式有何关系?
(2)这几个代数式中,
哪一个代
数式最简单?
问题2:
(3)能否把其余几个代数式化简?
10-(
a+b)=10-a-b
2x+(
x+1)=2x+x+1
4x-(
x-1)=4x-x+1
+
+
+
-(
)
-(
)
+(
)
“(
)”前是“
+”去掉“
+(
)”,
括号内各项的符号都不变;
“(
)”
前是“
-”去掉“
-(
)”,
括号内各项的符号都改变;
用字母表示为:
去括号法则:
a
+
(b
+
c)
=
;
a
-
(b
+
c)
=
;
都不变
都改变
a
+
b
+
c
a
–
b
-
c
例题讲解
例1:去括号并合并同类项:
(1)
(2)
(3)
(1)
(2)
(3)
(4)
化简下列各式:
随堂练习
③
代数式去括号后,都必须经过合并同类项,其结果才能简洁。
②
括号前是否有乘数
①
去括号后是否变号
去
括
号,看符号
是“+”号,不变号
是“-”号,全变号?
括号前有乘数
先把乘数乘到括号里面,然后再去括号
下列去括号正确吗?
(1)3a-(5b-2c+1)=3a-5b+2c-1
(2)x+3(y-w)=x+3y-w
(3)x-2(-y+m)=x+2y+m
(4)-(a-2b)+(c-2)=-a-2b+c-2
x+3y-3w
x+2y-2m
-a+2b+c-2
小结
1、去括号的依据是什么?
2、去括号时我们要注意哪些问题?
“乘法对加法的分配律”
①
是否变号
②
括号前是否有数乘;
③
代数式去括号后,都必须经过合并同类项,使其结果达到最简。
去
括
号,看符号
是“+”号,不变号
是“-”号,全变号
作业
课本:P122
习题第
1、2题
学习如逆水行舟,不进则退。你是最棒的!
引入新课
问题1:小聪带了10元钱去商店购物,花了a元买文具盒,b元买铅笔,他剩下的钱可以用代数式表示为_____________
10-(a+b)
10-a-b
10-(a+b)
10-a-b
=
新
课
情景1:如图,
要
搭x个正方形,需
要多少根火柴棒?
……
可用代数式表示为:
4x-(x-1),2x+(x+1),3x+1
x个
(1)上述几个代数式有何关系?
(2)这几个代数式中,
哪一个代
数式最简单?
问题2:
(3)能否把其余几个代数式化简?
10-(
a+b)=10-a-b
2x+(
x+1)=2x+x+1
4x-(
x-1)=4x-x+1
+
+
+
-(
)
-(
)
+(
)
“(
)”前是“
+”去掉“
+(
)”,
括号内各项的符号都不变;
“(
)”
前是“
-”去掉“
-(
)”,
括号内各项的符号都改变;
用字母表示为:
去括号法则:
a
+
(b
+
c)
=
;
a
-
(b
+
c)
=
;
都不变
都改变
a
+
b
+
c
a
–
b
-
c
例题讲解
例1:去括号并合并同类项:
(1)
(2)
(3)
(1)
(2)
(3)
(4)
化简下列各式:
随堂练习
③
代数式去括号后,都必须经过合并同类项,其结果才能简洁。
②
括号前是否有乘数
①
去括号后是否变号
去
括
号,看符号
是“+”号,不变号
是“-”号,全变号?
括号前有乘数
先把乘数乘到括号里面,然后再去括号
下列去括号正确吗?
(1)3a-(5b-2c+1)=3a-5b+2c-1
(2)x+3(y-w)=x+3y-w
(3)x-2(-y+m)=x+2y+m
(4)-(a-2b)+(c-2)=-a-2b+c-2
x+3y-3w
x+2y-2m
-a+2b+c-2
小结
1、去括号的依据是什么?
2、去括号时我们要注意哪些问题?
“乘法对加法的分配律”
①
是否变号
②
括号前是否有数乘;
③
代数式去括号后,都必须经过合并同类项,使其结果达到最简。
去
括
号,看符号
是“+”号,不变号
是“-”号,全变号
作业
课本:P122
习题第
1、2题
学习如逆水行舟,不进则退。你是最棒的!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
