二次函数回顾与思考(一)(四川省达川地区达县)
文档属性
| 名称 | 二次函数回顾与思考(一)(四川省达川地区达县) |

|
|
| 格式 | rar | ||
| 文件大小 | 740.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-16 00:00:00 | ||
图片预览





文档简介
课件12张PPT。二次函数
--回顾与思考
(一)
渡市中学 谢良文复习过程一、结合例题精析,强化练习,剖析知识点
1.二次函数的概念,二次函数y=ax2 (a≠0)的图象性质。 学生活动:学生四人一组进行讨论,并回顾例题所涉及的知识点,让学生代表发言分析解题方法,以及涉及的知识点。 (1) 是关于x的二次函数,则m2+m-4=2,且m+2≠0即:
m2+m-4=2,m+2≠0,解得;m=2或m=-3,m≠-2教师精析点评,二次函数的一般式为y=ax2+bx+c(a≠0)。强调a≠0.而常数b、c可以为0,当b,c同时为0时,抛物线为
y=ax2(a≠0)。此时,抛物线顶点为(0,0),对称轴是y轴,即直线x=0。 例:已知函数 是关于x的二次函数,求;
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点.这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是什么?这时当x为何值时,y随x的增大而减小? 教师归纳点评:
(1)教师在学生合作讨论基础上强调配方的方法及配方的意义,指出抛物线的一般式与顶点式的互化关系:(2)抛物线有最低点的条件是它开口向上,即m+2>0, (3)函数有最大值的条件是抛物线开口向下,即m+2<0。强化练习;已知函数 是二次函数,其图象开口方向向下,则m=_____ ,顶点为_____,当x_____0时,y随x的增大而增大,当x_____0时,y随x的增大而减小。 抛物线的增减性要结合图象进行分析,要求学生画出草图,渗透数形结合思想,进行观察分析。y=-3(x+1)2+112。用配方法求抛物线的顶点,对称轴;抛物线的画法,平移规律,例:用配方法求出抛物线y=-3x2-6x+8的顶点坐标、对称轴,并画出函数图象,说明通过怎样的平移,可得到抛物线
y=-3x2。学生活动:小组讨论配方方法,确定抛物线画法的步骤,探索平移的规律。充分讨论后,让学生代表归纳解题方法与思路。> < (0,0) -2 议一议
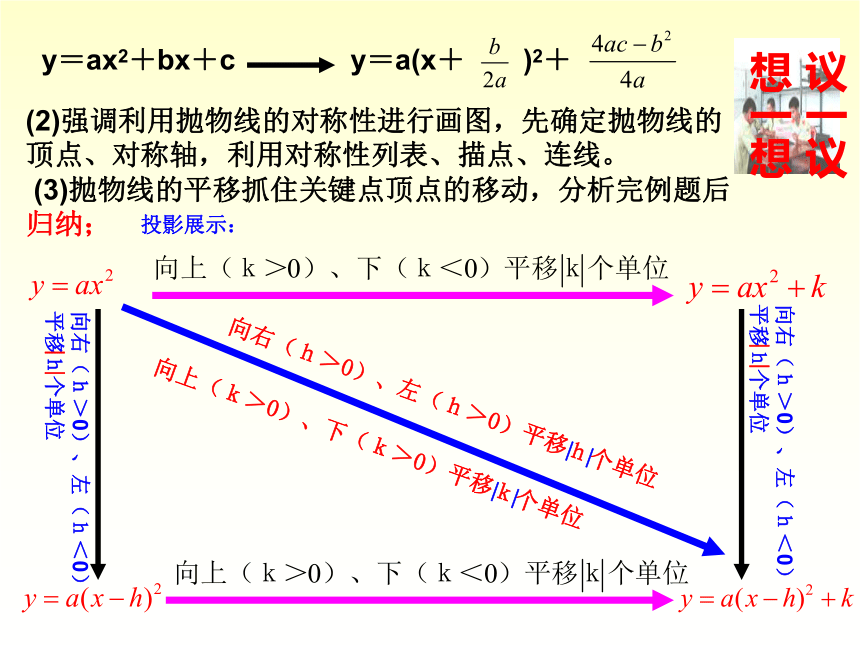
想一想(2)强调利用抛物线的对称性进行画图,先确定抛物线的顶点、对称轴,利用对称性列表、描点、连线。
(3)抛物线的平移抓住关键点顶点的移动,分析完例题后归纳;投影展示: 强化练习:
(1)抛物线y=x2+bx+c的图象向左平移2个单位。再向上平移3个单位,得抛物线y=x2-2x+1,求:b与c的值。
(2)通过配方,求抛物线y=x2-4x+5的开口方向、对称轴及顶点坐标,再画出图象。3.知识点串联,综合应用。
例:如图,已知直线AB经过x轴上的点A(2,0),且与抛物线
y=ax2相交于B、C两点,已知B点坐标为(1,1)。(1)b=6,c=-6教师点评:(1)直线AB过点A(2,0),B(1,1),代入解析式y=kx+b,可确定k、b,抛物线y=ax2过点B(1,1),代人可确定a。
求得:直线解析式为y=-x+2,抛物线解析式为y=x2。(2)向上;x=2;(2,1)学生活动:开展小组讨论,体验用待定系数法求函数的解析式。 (1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。议一议
想一想强化练习:函数y=ax2(a≠0)与直线y=2x-3
交于点A(1,b),求:
(1)a和b的值;
(2)求抛物线y=ax2的顶点和对称轴;
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大,
(4)求抛物线与直线y=-2两交点及抛物线的顶点所构成的三角形面积。(2)由y=-x+2与y=x2,先求抛物线与直线的另一个交点C的坐标为(-2,4),
S△OBC=S△AOC-S△OAB=3。
∵ S△AOD=S△OBC,且OA=2 ∴ D的纵坐标为3
又∵ D在抛物线y=x2上,∴x2=3,
即x=± ∴ D(- ,3)或( ,3)试一试
想一想二、课堂小结
1.让学生反思本节教学过程,归纳本节课复习过的知识点及应用。
2。投影:完成下表:(1)a=b=-1;(2)顶点(0,0),对称轴:y轴;
(3)x<0;(4)三角形面积为2(-2,4)(2,0)(1,1)三、作业
P26、27复习题.A组:1、2、3、4、5、6。课后反思:
本节课通过典型例题分折与强化训练相结合,重点复习了二次函数的概念,抛物线y=ax2(a≠0)的图象性质,配方法求抛物线的顶点与对称轴,并由此画出二次函数的图象,复习过程充分体现学生主导,让学生在合作学习中回忆学过的知识。其中,二次函数的定义中a≠0的条件学生易忽视,教师要给予强调,抛物线的平移是个难点,教师要引导学生结合图象,抓住顶点的变化进行平移。试一试
想一想向下向上y轴原点原点y轴X>0
x↗y↗X=0时,有最小值是y=0X<0
x↗y↘X<0
x↗y↗X>0
x↗y↘X=0时,有最大值是y=0议一议
想一想X=-1(-1,11)第一课时作业优化设计 一、填空。
1.若二次函数y=(m+1)x2+m2-2m-3的图象经过原点,则m=______。
2.函数y=3x2与直线y=kx+3的交点为(2,b),则k=______,b=______。
3.抛物线y=- (x-1)2+2可以由抛物线y=- x2向______方向平移______个单位,再向______方向平移______个单位得到。
4.用配方法把y=- x2+x- 化为y=a(x-h)2+k的形式为y=__________________,其开口方向______,对称轴为______,顶点坐标为______。
二、选择。
1.函数y=(m-n)x2+mx+n是二次函数的条件是( )A.m、n是常数,且m≠0 B.m、n是常数,且m≠n
C. m、n是常数,且n≠0 D. m、n可以为任意实数
2.直线y=mx+1与抛物线y=2x2-8x+k+8相交于点(3,4),则m、k值为( ) 三、解答题。
1.函数
(1)当a取什么值时,它为二次函数
(2)当a取什么值时,它为一次函数。
2.已知抛物线y=x2和直线y=ax+1
(1)求证:不论a取何值,抛物线与直线必有两个不同的交点。
(2)设A(x1,y1),B(x2,y2)是抛物线与直线的两个交点,P为线段AB的中点,且点P的横坐标为 ,试用a表示点P的纵坐标。3.下列图象中,当ab>0时,函数y=ax2与y=ax+b的图象是( )(3)过点C(0,-1)作直线L平行于x轴,试判断直线L与以AB为直径的圆的位置关系,并说明理由。 学习数学是为了探索宇宙的奥秘。同学们,让我们为了探索宇宙的奥秘,努力学好数学吧!
--回顾与思考
(一)
渡市中学 谢良文复习过程一、结合例题精析,强化练习,剖析知识点
1.二次函数的概念,二次函数y=ax2 (a≠0)的图象性质。 学生活动:学生四人一组进行讨论,并回顾例题所涉及的知识点,让学生代表发言分析解题方法,以及涉及的知识点。 (1) 是关于x的二次函数,则m2+m-4=2,且m+2≠0即:
m2+m-4=2,m+2≠0,解得;m=2或m=-3,m≠-2教师精析点评,二次函数的一般式为y=ax2+bx+c(a≠0)。强调a≠0.而常数b、c可以为0,当b,c同时为0时,抛物线为
y=ax2(a≠0)。此时,抛物线顶点为(0,0),对称轴是y轴,即直线x=0。 例:已知函数 是关于x的二次函数,求;
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点.这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是什么?这时当x为何值时,y随x的增大而减小? 教师归纳点评:
(1)教师在学生合作讨论基础上强调配方的方法及配方的意义,指出抛物线的一般式与顶点式的互化关系:(2)抛物线有最低点的条件是它开口向上,即m+2>0, (3)函数有最大值的条件是抛物线开口向下,即m+2<0。强化练习;已知函数 是二次函数,其图象开口方向向下,则m=_____ ,顶点为_____,当x_____0时,y随x的增大而增大,当x_____0时,y随x的增大而减小。 抛物线的增减性要结合图象进行分析,要求学生画出草图,渗透数形结合思想,进行观察分析。y=-3(x+1)2+112。用配方法求抛物线的顶点,对称轴;抛物线的画法,平移规律,例:用配方法求出抛物线y=-3x2-6x+8的顶点坐标、对称轴,并画出函数图象,说明通过怎样的平移,可得到抛物线
y=-3x2。学生活动:小组讨论配方方法,确定抛物线画法的步骤,探索平移的规律。充分讨论后,让学生代表归纳解题方法与思路。> < (0,0) -2 议一议
想一想(2)强调利用抛物线的对称性进行画图,先确定抛物线的顶点、对称轴,利用对称性列表、描点、连线。
(3)抛物线的平移抓住关键点顶点的移动,分析完例题后归纳;投影展示: 强化练习:
(1)抛物线y=x2+bx+c的图象向左平移2个单位。再向上平移3个单位,得抛物线y=x2-2x+1,求:b与c的值。
(2)通过配方,求抛物线y=x2-4x+5的开口方向、对称轴及顶点坐标,再画出图象。3.知识点串联,综合应用。
例:如图,已知直线AB经过x轴上的点A(2,0),且与抛物线
y=ax2相交于B、C两点,已知B点坐标为(1,1)。(1)b=6,c=-6教师点评:(1)直线AB过点A(2,0),B(1,1),代入解析式y=kx+b,可确定k、b,抛物线y=ax2过点B(1,1),代人可确定a。
求得:直线解析式为y=-x+2,抛物线解析式为y=x2。(2)向上;x=2;(2,1)学生活动:开展小组讨论,体验用待定系数法求函数的解析式。 (1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。议一议
想一想强化练习:函数y=ax2(a≠0)与直线y=2x-3
交于点A(1,b),求:
(1)a和b的值;
(2)求抛物线y=ax2的顶点和对称轴;
(3)x取何值时,二次函数y=ax2中的y随x的增大而增大,
(4)求抛物线与直线y=-2两交点及抛物线的顶点所构成的三角形面积。(2)由y=-x+2与y=x2,先求抛物线与直线的另一个交点C的坐标为(-2,4),
S△OBC=S△AOC-S△OAB=3。
∵ S△AOD=S△OBC,且OA=2 ∴ D的纵坐标为3
又∵ D在抛物线y=x2上,∴x2=3,
即x=± ∴ D(- ,3)或( ,3)试一试
想一想二、课堂小结
1.让学生反思本节教学过程,归纳本节课复习过的知识点及应用。
2。投影:完成下表:(1)a=b=-1;(2)顶点(0,0),对称轴:y轴;
(3)x<0;(4)三角形面积为2(-2,4)(2,0)(1,1)三、作业
P26、27复习题.A组:1、2、3、4、5、6。课后反思:
本节课通过典型例题分折与强化训练相结合,重点复习了二次函数的概念,抛物线y=ax2(a≠0)的图象性质,配方法求抛物线的顶点与对称轴,并由此画出二次函数的图象,复习过程充分体现学生主导,让学生在合作学习中回忆学过的知识。其中,二次函数的定义中a≠0的条件学生易忽视,教师要给予强调,抛物线的平移是个难点,教师要引导学生结合图象,抓住顶点的变化进行平移。试一试
想一想向下向上y轴原点原点y轴X>0
x↗y↗X=0时,有最小值是y=0X<0
x↗y↘X<0
x↗y↗X>0
x↗y↘X=0时,有最大值是y=0议一议
想一想X=-1(-1,11)第一课时作业优化设计 一、填空。
1.若二次函数y=(m+1)x2+m2-2m-3的图象经过原点,则m=______。
2.函数y=3x2与直线y=kx+3的交点为(2,b),则k=______,b=______。
3.抛物线y=- (x-1)2+2可以由抛物线y=- x2向______方向平移______个单位,再向______方向平移______个单位得到。
4.用配方法把y=- x2+x- 化为y=a(x-h)2+k的形式为y=__________________,其开口方向______,对称轴为______,顶点坐标为______。
二、选择。
1.函数y=(m-n)x2+mx+n是二次函数的条件是( )A.m、n是常数,且m≠0 B.m、n是常数,且m≠n
C. m、n是常数,且n≠0 D. m、n可以为任意实数
2.直线y=mx+1与抛物线y=2x2-8x+k+8相交于点(3,4),则m、k值为( ) 三、解答题。
1.函数
(1)当a取什么值时,它为二次函数
(2)当a取什么值时,它为一次函数。
2.已知抛物线y=x2和直线y=ax+1
(1)求证:不论a取何值,抛物线与直线必有两个不同的交点。
(2)设A(x1,y1),B(x2,y2)是抛物线与直线的两个交点,P为线段AB的中点,且点P的横坐标为 ,试用a表示点P的纵坐标。3.下列图象中,当ab>0时,函数y=ax2与y=ax+b的图象是( )(3)过点C(0,-1)作直线L平行于x轴,试判断直线L与以AB为直径的圆的位置关系,并说明理由。 学习数学是为了探索宇宙的奥秘。同学们,让我们为了探索宇宙的奥秘,努力学好数学吧!
