等差数列
图片预览





文档简介
课件16张PPT。等差数列
(第一课时)人教版第一册(上)请看以下几例:
4,5,6,7,8,9,10,······
3,0,-3,-6,-9,-12,······
1/10,2/10,3/10,4/10,5/10······
3,3,3,3,3,3,3,······你还记得吗?数列的定义
给出数列的方法
等差数列的定义 一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差。公差通常用字母d表示。等差数列的公差 d:
1.an-an-1=d (n≥2)(数学表达式)
3.d的范围 d∈R2.常数 如2,3,5,9,11就不是等差数列等差数列的通项公式 如果等差数列{an}的首项是 ,公差是d,那么根据等差数列的定义得到:
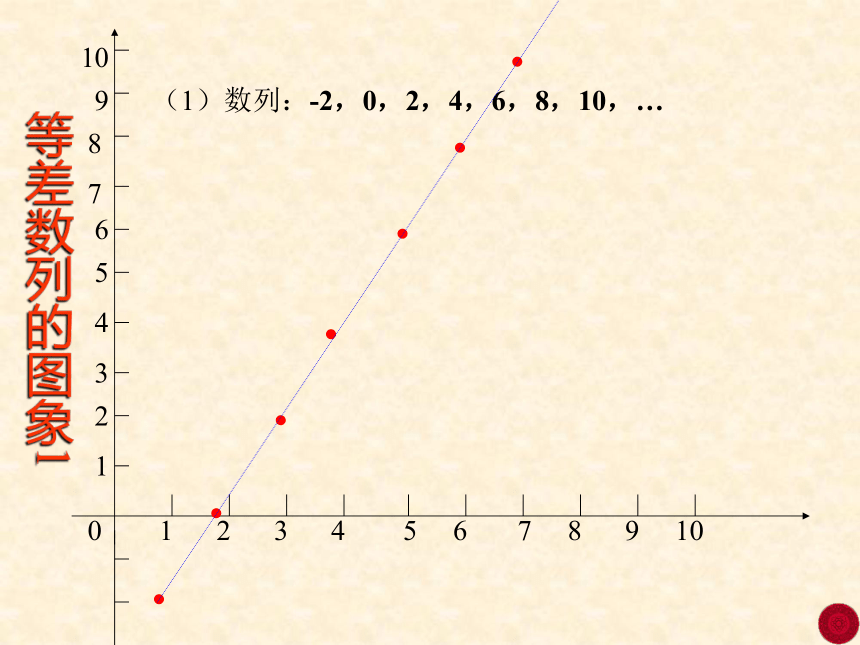
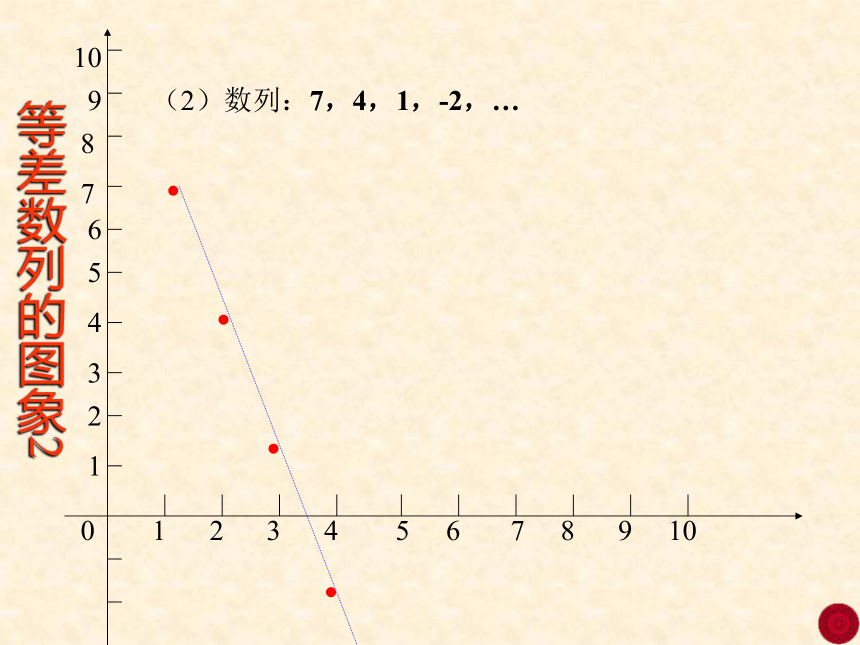
a2=a1+d 由此得到 an=a1+(n-1)d返回an-a1=(n-1)dan-an-1=da4-a3=da3-a2=dan=a1+(n-1)da4=a1+3da3=a1+2da2-a1=d等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(1)数列:4,4,4,4,4,4,4,…●●●●●●●●●●课堂练习(一)在等差数列{an}中,
1)已知a1=2,d=3,n=10,求an解:a10=a1+9d=2+9×3=292)已知a1=3,an=21,d=2,求n解:21=3+(n-1)×2 n=103)已知a1=12,a6=27,求d解:a6=a1+5d,即27=12+5d d=34)已知d=-1/3,a7=8,求a1解:a7=a1+6d 8=a1+6×(-1/3)
∴a1=10课堂练习二1 已知等差数列 中, 求
法一法二2 考虑等差数列 中 与 关系等差数列的应用 例1. 1)等差数列8,5,2,······的第20项是几?
2)-401是不是等差数列-5,-9,-13······的项?如果是,是第几项?解: 1)由题意得,a1=8,d=-3 2)由题意得,a1=-5,d=-4,an=-401an=a1+(n-1)d∴n=100
∴-401是这个数列的第100项。∴a20=a1+19d=8+19×(-3)=-49-401=-5+(n-1)×(-4) 3)-20是不是等差数列0,-3.5,-7···的项?如果是,是第几项?如果不是,说明理由。解:a1=0,d=-3.5∴-20不是这个数列中的项。n=47/7-20=0+(n-1)×(-3.5)等差数列的应用 例2.在等差数列{an}中,已知a5=10,a12=31,求首项a1与公差d。解:由题意,a5=a1+4d
a12=a1+11d解之得 a1=-2 d=3若让求a7,怎样求?即 10=a1+4d
31=a1+11d课堂练习(三) 2.在等差数列{an}中,已知a3=9,a9=3,求a12答案:a12=0 1.在等差数列{an}中,已知a2=3,a4=7,求a6、a8解:由题意得,a1+d=3, a1+3d=7∴a6=a1+5d=1+5×2=11
a8=a1+7d=1+7×2=15∴ a1=1, d=2本节小结 1.等差数列的定义你都掌握了吗?2.等差数列的通项公式及其应用作业作业 习题3.2 1,2,6,8应用延伸 1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是多少?解:由题意得,
a6=a1+5d>0 a7=a1+6d<0 2.已知等差数列{an}的首项为30,这个数列从第12项起为负数,求公差d的范围。解:a12=30+11d<0
a11=30+10d≥0∵d∈Z ∴d=-4∴-23/5<d<-23/6 ∴ -3≤d<-30/11
即公差d的范围为:-3≤d<-30/11
4,5,6,7,8,9,10,······
3,0,-3,-6,-9,-12,······
1/10,2/10,3/10,4/10,5/10······
3,3,3,3,3,3,3,······你还记得吗?数列的定义
给出数列的方法
等差数列的定义 一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差。公差通常用字母d表示。等差数列的公差 d:
1.an-an-1=d (n≥2)(数学表达式)
3.d的范围 d∈R2.常数 如2,3,5,9,11就不是等差数列等差数列的通项公式 如果等差数列{an}的首项是 ,公差是d,那么根据等差数列的定义得到:
a2=a1+d 由此得到 an=a1+(n-1)d返回an-a1=(n-1)dan-an-1=da4-a3=da3-a2=dan=a1+(n-1)da4=a1+3da3=a1+2da2-a1=d等差数列的图象1(1)数列:-2,0,2,4,6,8,10,…●●●●●●●等差数列的图象2(2)数列:7,4,1,-2,…●●●●等差数列的图象3(1)数列:4,4,4,4,4,4,4,…●●●●●●●●●●课堂练习(一)在等差数列{an}中,
1)已知a1=2,d=3,n=10,求an解:a10=a1+9d=2+9×3=292)已知a1=3,an=21,d=2,求n解:21=3+(n-1)×2 n=103)已知a1=12,a6=27,求d解:a6=a1+5d,即27=12+5d d=34)已知d=-1/3,a7=8,求a1解:a7=a1+6d 8=a1+6×(-1/3)
∴a1=10课堂练习二1 已知等差数列 中, 求
法一法二2 考虑等差数列 中 与 关系等差数列的应用 例1. 1)等差数列8,5,2,······的第20项是几?
2)-401是不是等差数列-5,-9,-13······的项?如果是,是第几项?解: 1)由题意得,a1=8,d=-3 2)由题意得,a1=-5,d=-4,an=-401an=a1+(n-1)d∴n=100
∴-401是这个数列的第100项。∴a20=a1+19d=8+19×(-3)=-49-401=-5+(n-1)×(-4) 3)-20是不是等差数列0,-3.5,-7···的项?如果是,是第几项?如果不是,说明理由。解:a1=0,d=-3.5∴-20不是这个数列中的项。n=47/7-20=0+(n-1)×(-3.5)等差数列的应用 例2.在等差数列{an}中,已知a5=10,a12=31,求首项a1与公差d。解:由题意,a5=a1+4d
a12=a1+11d解之得 a1=-2 d=3若让求a7,怎样求?即 10=a1+4d
31=a1+11d课堂练习(三) 2.在等差数列{an}中,已知a3=9,a9=3,求a12答案:a12=0 1.在等差数列{an}中,已知a2=3,a4=7,求a6、a8解:由题意得,a1+d=3, a1+3d=7∴a6=a1+5d=1+5×2=11
a8=a1+7d=1+7×2=15∴ a1=1, d=2本节小结 1.等差数列的定义你都掌握了吗?2.等差数列的通项公式及其应用作业作业 习题3.2 1,2,6,8应用延伸 1.一个首项为23,公差为整数的等差数列,如果前六项均为正数,第七项起为负数,则它的公差是多少?解:由题意得,
a6=a1+5d>0 a7=a1+6d<0 2.已知等差数列{an}的首项为30,这个数列从第12项起为负数,求公差d的范围。解:a12=30+11d<0
a11=30+10d≥0∵d∈Z ∴d=-4∴-23/5<d<-23/6 ∴ -3≤d<-30/11
即公差d的范围为:-3≤d<-30/11
