三角形内角和定理(山东省烟台市牟平区)
文档属性
| 名称 | 三角形内角和定理(山东省烟台市牟平区) |  | |
| 格式 | rar | ||
| 文件大小 | 305.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-30 11:06:00 | ||
图片预览

文档简介
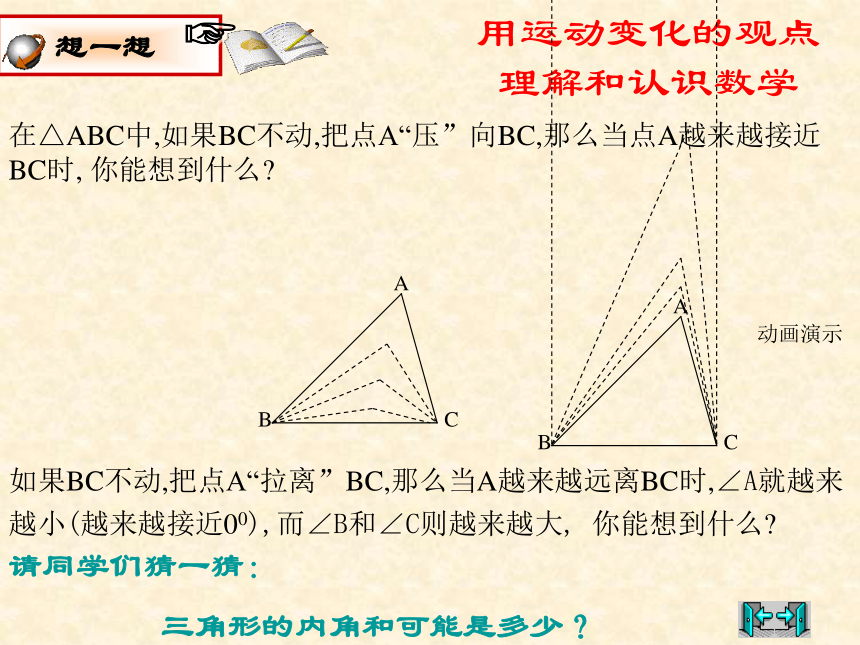
课件16张PPT。第三章 证明(一)三角形内角和定理的证明山东省烟台市牟平区文化第一初级中学数学组用运动变化的观点理解和认识数学在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, 你能想到什么?如果BC不动,把点A“拉离”BC,那么当A越来越远离BC时,∠A就越来越小(越来越接近00),而∠B和∠C则越来越大, 你能想到什么? 动画演示请同学们猜一猜:
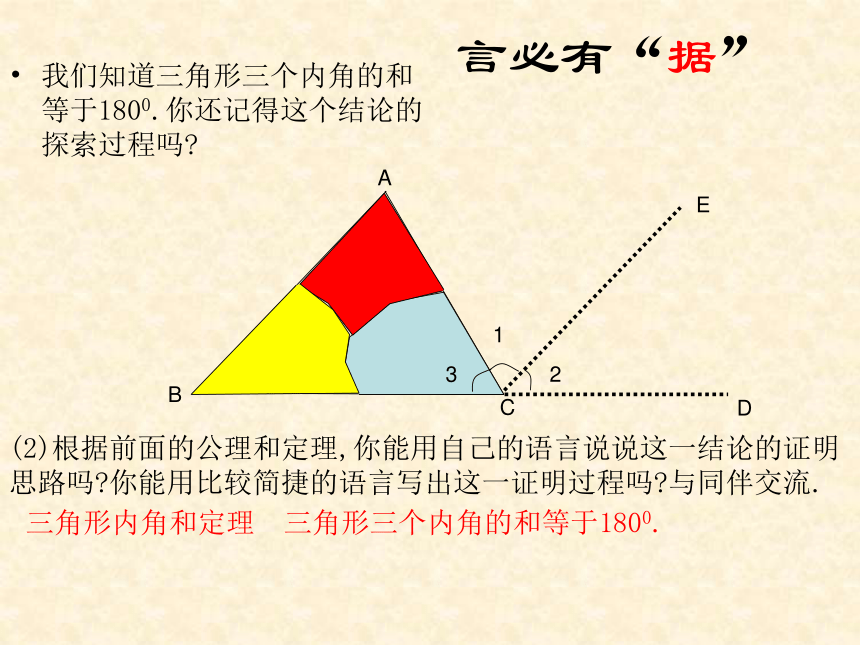
三角形的内角和可能是多少?ABCDE我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.三角形内角和定理 三角形三个内角的和等于1800.言必有“据”“行家” 看“门道”已知:如图,△ABC.
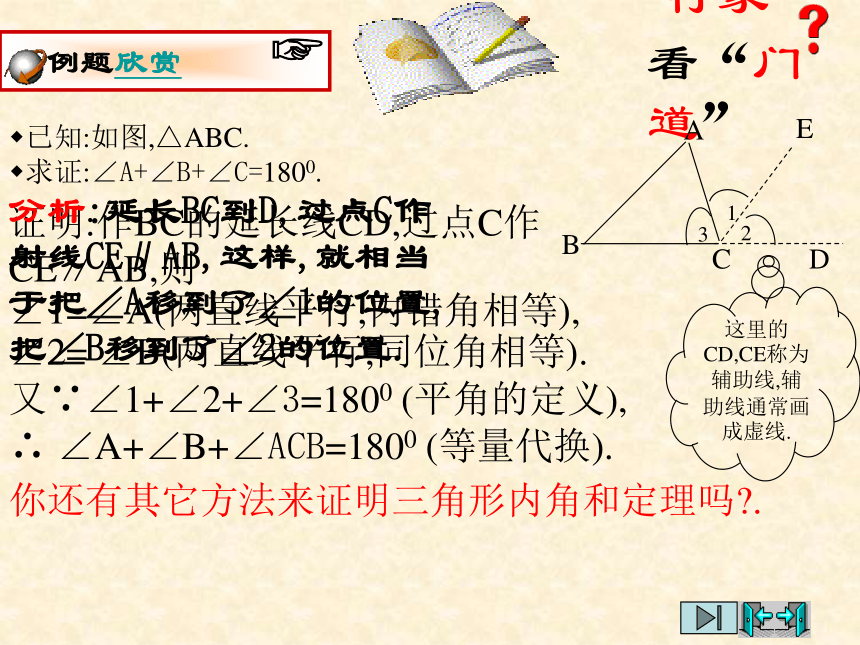
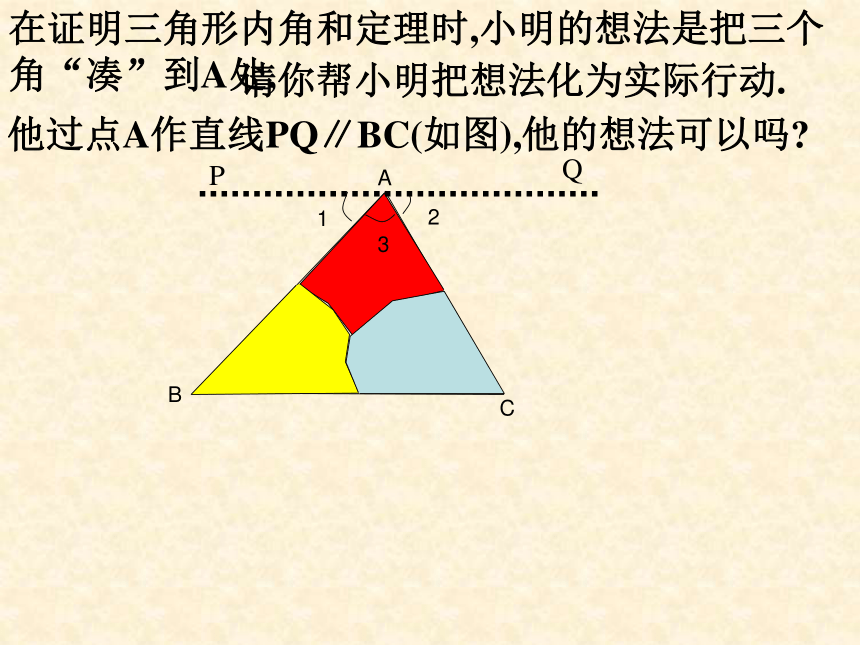
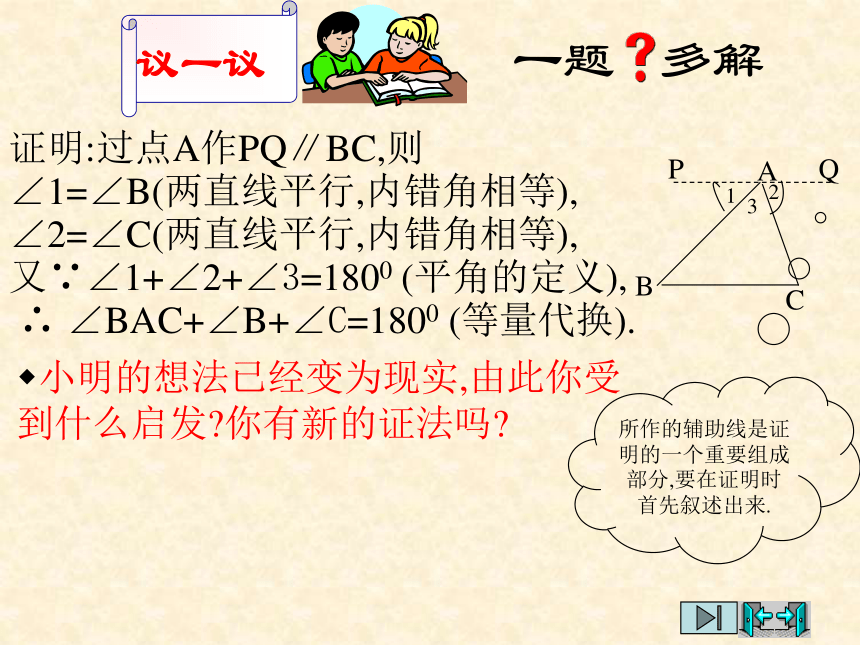
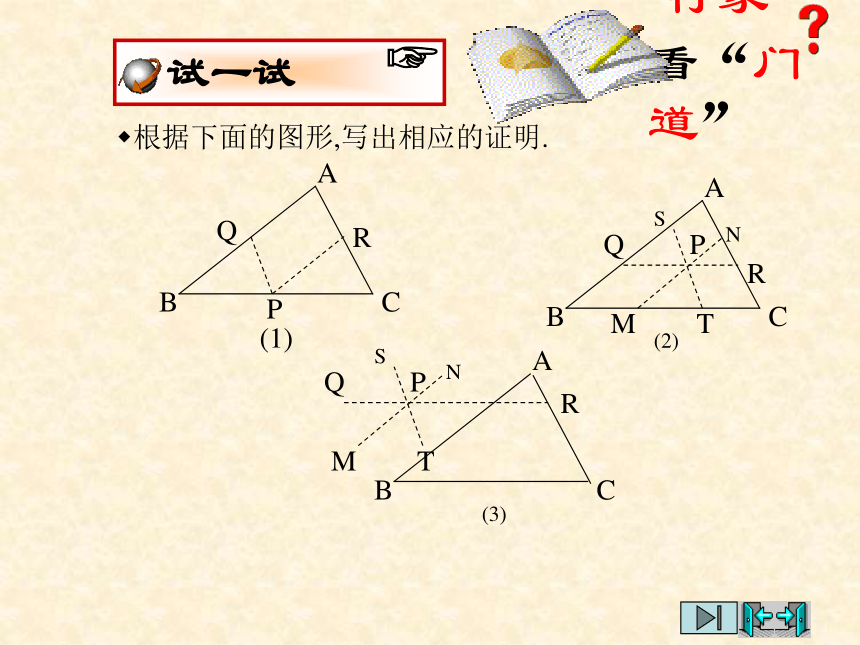
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则你还有其它方法来证明三角形内角和定理吗?.∠1=∠A(两直线平行,内错角相等),∠2= ∠B(两直线平行,同位角相等).又∵∠1+∠2+∠3=1800 (平角的定义),∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABCPQ在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,请你帮小明把想法化为实际行动.他过点A作直线PQ∥BC(如图),他的想法可以吗?一题 多解小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则∠1=∠B(两直线平行,内错角相等),∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.“行家” 看“门道”根据下面的图形,写出相应的证明.三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 我是最棒的1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500.结论: 直角三角形的两个锐角互余.以后可以直接运用.回味无穷掌握几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理.
结论: 直角三角形的两个锐角互余.
探索证明的思路的方法: 由“因”导“果”,执“果”索“因”.
与同伴交流,你是如何提高证明命题能力的.1、如图,已知△ABC中, ∠B 和∠C的平分线BE,CF交点O. 求证: ∠BOC=90°+2 、 如图,已知AD是△ABD
和△ACD的公共边.
求证:∠BDC=∠BAC+∠B+∠C2 、 如图,已知AD是△ABD
和△ACD的公共边.
求证:∠BDC=∠BAC+∠B+∠C证法二:思考题:如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD(用两种方法证明)知识的升华P90习题3.7 1,2,3题;
祝你成功!结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”.是探索证明思路的基本方法.
三角形的内角和可能是多少?ABCDE我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗?(2)根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗?你能用比较简捷的语言写出这一证明过程吗?与同伴交流.三角形内角和定理 三角形三个内角的和等于1800.言必有“据”“行家” 看“门道”已知:如图,△ABC.
求证:∠A+∠B+∠C=1800.证明:作BC的延长线CD,过点C作CE∥AB,则你还有其它方法来证明三角形内角和定理吗?.∠1=∠A(两直线平行,内错角相等),∠2= ∠B(两直线平行,同位角相等).又∵∠1+∠2+∠3=1800 (平角的定义),∴ ∠A+∠B+∠ACB=1800 (等量代换).分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.这里的CD,CE称为辅助线,辅助线通常画成虚线.ABCPQ在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,请你帮小明把想法化为实际行动.他过点A作直线PQ∥BC(如图),他的想法可以吗?一题 多解小明的想法已经变为现实,由此你受到什么启发?你有新的证法吗?证明:过点A作PQ∥BC,则∠1=∠B(两直线平行,内错角相等),∠2=∠C(两直线平行,内错角相等),又∵∠1+∠2+∠3=1800 (平角的定义), ∴ ∠BAC+∠B+∠C=1800 (等量代换).所作的辅助线是证明的一个重要组成部分,要在证明时首先叙述出来.“行家” 看“门道”根据下面的图形,写出相应的证明.三角形内角和定理三角形内角和定理 三角形三个内角的和等于1800.
△ABC中,∠A+∠B+∠C=1800.∠A+∠B+∠C=1800的几种变形:
∠A=1800 –(∠B+∠C).
∠B=1800 –(∠A+∠C).
∠C=1800 –(∠A+∠B).
∠A+∠B=1800-∠C.
∠B+∠C=1800-∠A.
∠A+∠C=1800-∠B.这里的结论,以后可以直接运用. 我是最棒的1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
求证: ∠ADE=500.结论: 直角三角形的两个锐角互余.以后可以直接运用.回味无穷掌握几何命题证明的方法,步骤,格式及注意事项.
三角形内角和定理.
结论: 直角三角形的两个锐角互余.
探索证明的思路的方法: 由“因”导“果”,执“果”索“因”.
与同伴交流,你是如何提高证明命题能力的.1、如图,已知△ABC中, ∠B 和∠C的平分线BE,CF交点O. 求证: ∠BOC=90°+2 、 如图,已知AD是△ABD
和△ACD的公共边.
求证:∠BDC=∠BAC+∠B+∠C2 、 如图,已知AD是△ABD
和△ACD的公共边.
求证:∠BDC=∠BAC+∠B+∠C证法二:思考题:如图,已知∠AMN+∠MNF+∠NFC=360°,
求证:AB∥CD(用两种方法证明)知识的升华P90习题3.7 1,2,3题;
祝你成功!结束寄语严格性之于数学家,犹如道德之于人.
由“因”导“果”,执“果”索“因”.是探索证明思路的基本方法.
