二次函数的系数与图象的关系

课件14张PPT。专题:
待定系数法
y=ax2+bx+c的系数与图象关系(一)特定函数中的待定系数例1. y=(m+3)x (1) m取什么值时,此函数是正比例函数? (2) m取什么值时,此函数是反比例函数? (3) m取什么值时,此函数是二次函数?m2－7 如果函数 y=(k-2) +kx+1是二次函数,则k的值一定是______0练习变式:已知 y =(m+1)x 　　是二次函数且其图象开口向上,(1)求m的值和函数解析式;(2)x在何范围内,y 随x的增大而增大? y随x的增大而减小? m2+m解: (1) 依题意有:m+1>0 ①m2+m=2 ②解②得:m1=－2, m2=1 由①得:m>－1∴ m=1 此时,二次函数为: y=2x2,(2) ∵ a=2>0,∴抛物线 y=2x2开口向上,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.下m+1<0 ①由①得:m<－1∴ m=－2 二次函数为: y=－x2(2) ∵ a=－1<0,∴抛物线 y=－x2开口向下,当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.m2+m=2 ②解②得:m1=－2, m2=1 (二)满足特定条件下的待定系数例2 按下列要求求出二次函数的解析式：
（1）已知抛物线y=ax2+c经过点（-3，2）（0，-1）求该抛物线线的解析式。变式:已知抛物线y=ax2+bx+c的截距为3,经过点（-2，-7）（1，2）求该抛物线线的解析式。该抛物线线的解析式为:y=-2x2+x+3。按下列要求求出二次函数的解析式：（2）抛物线与y=-2x2-6x+3的图象相交于y轴，顶点坐标是（-1，3）的抛物线解析式。变式:抛物线对称轴是直线x=-1，顶点纵坐标是-3，且经过（1，2）的点的解析式.函数y=ax2的图像与直线y=x-1有一个交点为（2，1）则函数y=4ax2的图像与直线y=x-1交点的个数为（ ）个
A ； 0 B ; 1 C; 2 D;3
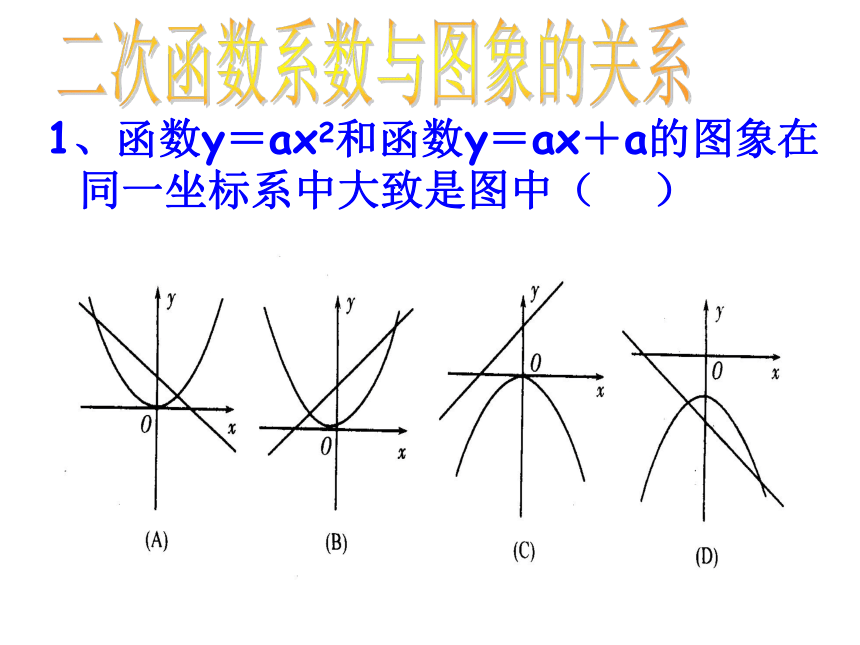
应用于简单的交点问题1、函数y＝ax2和函数y＝ax＋a的图象在同一坐标系中大致是图中（ ）二次函数系数与图象的关系2、在同一直角坐标系中，一次函数y=ax+c和
二次函数y=ax2+c的图象大致是如图中的（ ）二次函数系数与图象的关系3.如图，在同一坐标系中，函数y=ax+b与y=ax2+bx(ab≠0)的图象只可能是（ ）二次函数系数与图象的关系4.已知抛物线y＝ax2＋bx＋c的图象如图所示，
下列结论：
①a+b+c<0 ②a-b+c>0 ③acb>0 ④b=2a,
其中正确的结论的个数是　　　（　　）
A.4 B.3 C.2 D.1二次函数系数与图象的关系5.二次函数y=ax2+bx+c的图象如图所示，下列各式中是正数的有（　　　　）a ② b ③ c
　a+b+c ⑤ a-b+c
⑥ 　4a+b ⑦ 2a+bA.5个　　B.4个
C.3个　　D.2个二次函数系数与图象的关系例2.用总长为60m的篱笆墙围成矩形场地，矩形面积S随矩形一边长L的变化而变化，当L多少时，场地的面积S最大？ ?实际应用(最值)1.如图，隧道横截面的下部是矩形，上部是半圆，周长为16米。
⑴求截面积S（米2）关于底部宽x（米）的函数解析式，及自变量x 的取值范围？
⑵试问：当底部宽x为几米时，隧道的截面积S最大（结果精确到0.01米）？课后拓展