1.1 生活中的立体图形 课后提升练(含解析) 2023-2024学年北师大版七年级数学上册
文档属性
| 名称 | 1.1 生活中的立体图形 课后提升练(含解析) 2023-2024学年北师大版七年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 16:58:21 | ||
图片预览


文档简介
1.1 生活中的立体图形 课后提升练
一、填空题
1.当笔尖在纸上移动时,形成 ,这说明: ;表针旋转时,形成了一个 ,这说明: ;长方形纸片绕它的一边旋转,形成的几何图形就是 ,这说明: .
2.如果一个六棱柱的一条侧棱长为5 cm,那么所有侧棱之和为 .
3.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体的体积为 cm3.(结果保留π)
4.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
5.李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为 .
6.两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,在这个新长方体中,体积是 cm3, 最大表面积是 cm2 .
二、选择题
7.下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )
A. B.
C. D.
8.直棱柱的侧面都是( )
A.正方形 B.长方形 C.五边形 D.以上都不对
9.下列几何体中棱柱的个数为( )
A.4个 B.2个 C.3个 D.1个
10.下列说法错误的是( )
A.长方体、正方体都是棱柱
B.三棱柱的侧面是三角形
C.直六棱柱有六个侧面且侧面为长方形
D.棱柱的底面都是多边形
11.下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )
A.直角三角形 B.等腰三角形 C.矩形 D.扇形
12.如图,用黑板擦擦黑板时,留下的痕迹是( )
A.点 B.线 C.面 D.体
13.“十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A.圆锥 B.圆柱 C.球 D.圆台
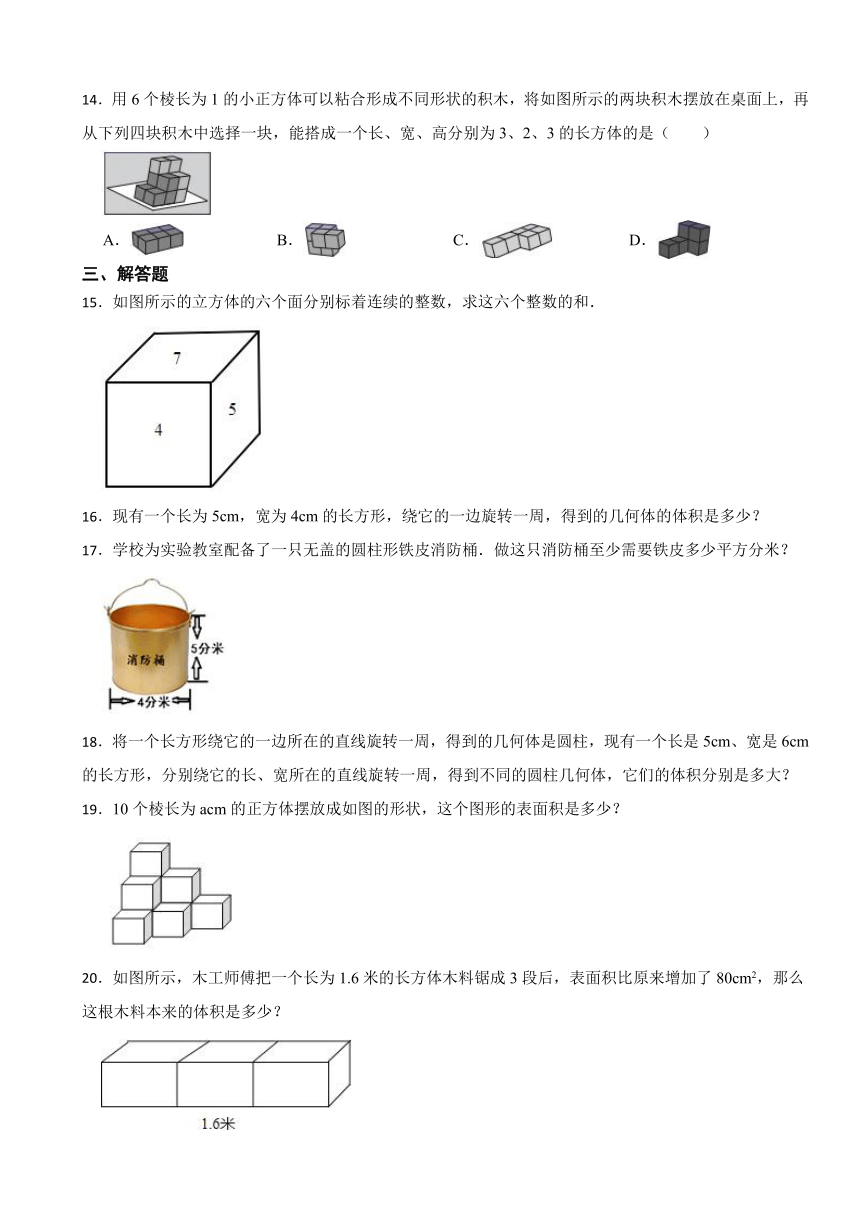
14.用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )
A. B. C. D.
三、解答题
15.如图所示的立方体的六个面分别标着连续的整数,求这六个整数的和.
16.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
17.学校为实验教室配备了一只无盖的圆柱形铁皮消防桶.做这只消防桶至少需要铁皮多少平方分米?
18.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现有一个长是5cm、宽是6cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱几何体,它们的体积分别是多大?
19.10个棱长为acm的正方体摆放成如图的形状,这个图形的表面积是多少?
20.如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2,那么这根木料本来的体积是多少?
答案解析部分
1.【答案】一条线;点动成 线;圆面;线动成面;圆柱体;面动成体
【解析】【解答】解:当笔尖在纸上移动时,形成直线,这说明:点动成线;表针旋转时,形成了一个圆面,这说明:线动成面;长方形纸片绕它的一边旋转,形成的几何图形就是圆柱,这说明:面动成体。
故答案为:直线,点动成线,圆面,线动成面,圆柱,面动成体.
【分析】根据点、线、面、体的含义进行作答即可。
2.【答案】30cm
【解析】【解答】∵六棱柱有6条棱,且每条棱的长度均为5 cm,∴所有侧棱之和=6×5 cm=30 cm.故答案为:30cm
【分析】六棱柱有6条棱,由每条棱的长度,求出侧棱之和.
3.【答案】27π
【解析】【解答】直线AB为轴,将正方形旋转一周可得圆柱体,圆柱的高为3 cm,底面直径为6 cm,∴所得几何体的体积=32π 3=27π,故答案为:27π
【分析】正方形旋转一周得到的是圆柱体,正方形的边长得到圆柱的高和底面直径,求出圆柱体的体积.
4.【答案】24
【解析】【解答】解:表面积是2×2×6=24.
故答案为:24.
【分析】挖去一个棱长为1的小正方体,通过平移的方法,可以发现得到的图形与原图形表面积相等,从而利用正方体的表面积计算方法算出答案。
5.【答案】33
【解析】【解答】解:根据题意得:
第一层露出的表面积为:1×1×6﹣1×1=5;
第二层露出的表面积为:1×1×6×4﹣1×1×13=11;
第三层露出的表面积为:1×1×6×9﹣1×1×37=17.
所以红色部分的面积为:5+11+17=33.
故答案为:33
【分析】根据表面积的计算方法,分层计算出每层需要染成红色的面积,再相加即可。
6.【答案】120;164
【解析】【解答】∵两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,
∴在这个新长方体中,体积是:2×(5×4×3)=120(cm3),
表面积有以下三种情形:
①.重叠的是长.宽分别为5cm,4cm的面,
则新长方体表面积是2×(5×4)+4×(5×3)+4×(4×3)=148(cm2);
②.重叠的是长.高分别为5cm,3cm的面,
则新长方体表面积是4×(5×4)+2×(5×3)+4×(4×3)=158(cm2);
③.重叠的是宽.高分别为4cm,3cm的面,
则新长方体表面积是4×(5×4)+4×(5×3)+2×(4×3)=164(cm2).
答:在这些新长方体中,表面积最大是164cm2
【分析】两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,这个新长方体无论怎样叠放,其体积都不会变化,就是原一个长方体的体积乘以2;但表面积就要分三种情况来讨论:①.重叠的是长.宽分别为5cm,4cm的面,②.重叠的是长.高分别为5cm,3cm的面,③.重叠的是宽.高分别为4cm,3cm的面,然后分别按长方体的表面积就是方法算出答案,再比较大小即可得出答案。
7.【答案】A
【解析】【解答】解:正方体不能由一个平面图形绕某直线旋转一周得到,故A满足题意;
球体可以由一个圆绕一条直径旋转一周得到,故B不满足题意;
圆锥可以由一个直角三角形绕一条直角边旋转一周得到,故C不满足题意;
圆柱可以由一个长方形绕一条边旋转一周得到,故D不满足题意.
故答案为:A.
【分析】根据点动成线、线动成面、面动成体的知识进行解答.
8.【答案】B
【解析】【解答】解:直棱柱不管从哪个侧面看都是长方形.
故答案为:B.
【分析】棱柱由上下两个底面以及侧面组成,上下两个底面可以是全等的多边形,侧面是四边形;棱长与底面垂直的棱柱叫直棱柱,据此即可得出答案.
9.【答案】B
【解析】【解答】解:根据棱柱的定义可知:①是四棱柱,③是三棱柱,其余的均不是棱柱,
故棱柱有个.
故答案为:B.
【分析】有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,据此判断.
10.【答案】B
【解析】【解答】解:A、长方体、正方体都是棱柱,不符合题意;
B、三棱柱的侧面是长方形,符合题意;
C、直六棱柱有六个侧面且侧面为长方形,不符合题意;
D、棱柱的底面都是多边形,不符合题意;
故答案为:B
【分析】根据棱柱的定义逐项判断即可。
11.【答案】B
【解析】【解答】解:沿着某一直线旋转180°后,一定能形成圆锥的是等腰三角形.
故答案为:B.
【分析】等腰三角形沿着底边上的高旋转一周可得到圆锥,据此判断.
12.【答案】C
【解析】【解答】解:黑板擦属于体,但留下的痕迹是表现在平面上而不是空间的,所以是面.
故答案为:C.
【分析】用黑板擦擦黑板时,留下的痕迹是表现在平面上的,据此判断.
13.【答案】C
【解析】【解答】当硬币在地面某位置快速旋转时,形成的几何体是球,
故答案为:C.
【分析】根据面动成体,故硬币在地面某位置旋转时,形成球体。
14.【答案】D
【解析】【解答】解:原积木所缺的几何体左视图为一个由4个棱长为1的小正方体组成的大正方体,所以可排除选项A和C;俯视图为一个由4个小正方体组成的L形,所以可排除选项B.
故答案为:D.
【分析】根据 用6个棱长为1的小正方体可以粘合形成不同形状的积木, 对每个选项一一判断即可。
15.【答案】解:∵已知三个面上的数字为4、5、7,且六个面分别标着连续的整数,∴这六个数中一定含有4、5、6、7,∴这六个数字可能为2、3、4、5、6、7;或3、4、5、6、7、8;或4、5、6、7、8、9;当这六个数为2、3、4、5、6、7时,其和为2+3+4+5+6+7=27;当这六个数为3、4、5、6、7、8时,其和为3+4+5+6+7+8=33;当这六个数为4、5、6、7、8、9时,其和为4+5+6+7+8+9=39;故答案为:27或33或39.
【解析】【分析】由于正方体的前面标注的是4,右面标注的是5,上面标注的是7,又六个面分别标着连续的整数,故这六个数中一定含有4、5、6、7,从而得出此题共有三种情况:这六个数字可能为2、3、4、5、6、7;或3、4、5、6、7、8;或4、5、6、7、8、9;然后根据有理数的加法法则分别算出其和即可。
16.【答案】解:以宽为旋转轴,V=π×52×4=100π;
以长为旋转轴,V=π×42×5=80π
【解析】【分析】根据面运动成体得出将长方形的一边旋转一周应该是一个圆柱,此题两种情况: 情况①以长为4的边旋转一周,所得圆柱的高就是4,底面圆的半径是5,根据圆柱的体积公式即可算出答案;情况②以长为5的边旋转一周,所得圆柱的高就是5,底面圆的半径是4,根据圆柱的体积公式即可算出答案;
17.【答案】解:π×4×5+π×(4÷2)2
=20π+4π
=24π(平方分米)
答:做这只消防桶至少需要铁皮24π平方分米.
【解析】【分析】由于水桶无盖,所以只求圆柱的侧面积和一个底面的面积和,根据圆柱的侧面积公式、圆的面积公式,把数据分别代入解答即可.
18.【答案】解:①绕长所在的直线旋转一周得到圆柱体积为:π×52×6=150π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×62×5=180π(cm3).
答:它们的体积分别是150π(cm3)和180π(cm3)
【解析】【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
19.【答案】解:6×6×(a×a)=36a2(cm2)
故这个图形的表面积是36a2cm2.
【解析】【分析】分别得到前后左右上下6个方向面的个数,再乘以一个面的面积即可求解.
20.【答案】3200cm3解答:∵把长方体木料锯成3段后,其表面积增加了四个截面,因此每个截面的面积为80÷4=20cm2,∴这根木料本来的体积是:1.6×100×20=3200(cm3)
【解析】【分析】根据长方体的切割特点:切割成三段后,表面积是增加了4个长方体的侧面的面积,求出这根木料的侧面积,再利用长方体的体积公式即可解答.
一、填空题
1.当笔尖在纸上移动时,形成 ,这说明: ;表针旋转时,形成了一个 ,这说明: ;长方形纸片绕它的一边旋转,形成的几何图形就是 ,这说明: .
2.如果一个六棱柱的一条侧棱长为5 cm,那么所有侧棱之和为 .
3.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体的体积为 cm3.(结果保留π)
4.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
5.李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为 .
6.两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,在这个新长方体中,体积是 cm3, 最大表面积是 cm2 .
二、选择题
7.下面的几何体中,哪一个不能由平面图形绕某直线旋转一周得到( )
A. B.
C. D.
8.直棱柱的侧面都是( )
A.正方形 B.长方形 C.五边形 D.以上都不对
9.下列几何体中棱柱的个数为( )
A.4个 B.2个 C.3个 D.1个
10.下列说法错误的是( )
A.长方体、正方体都是棱柱
B.三棱柱的侧面是三角形
C.直六棱柱有六个侧面且侧面为长方形
D.棱柱的底面都是多边形
11.下列图形沿着某一直线旋转180°后,一定能形成圆锥的是( )
A.直角三角形 B.等腰三角形 C.矩形 D.扇形
12.如图,用黑板擦擦黑板时,留下的痕迹是( )
A.点 B.线 C.面 D.体
13.“十一黄金周”期间,小明和小亮相约去太原植物园游玩,中途两人口渴了,于是小明提议通过在地面旋转硬币的方法决定谁去买水,在旋转硬币时小明发现:当硬币在地面某位置快速旋转时,形成了一个几何体,请问这个几何体是( )
A.圆锥 B.圆柱 C.球 D.圆台
14.用6个棱长为1的小正方体可以粘合形成不同形状的积木,将如图所示的两块积木摆放在桌面上,再从下列四块积木中选择一块,能搭成一个长、宽、高分别为3、2、3的长方体的是( )
A. B. C. D.
三、解答题
15.如图所示的立方体的六个面分别标着连续的整数,求这六个整数的和.
16.现有一个长为5cm,宽为4cm的长方形,绕它的一边旋转一周,得到的几何体的体积是多少?
17.学校为实验教室配备了一只无盖的圆柱形铁皮消防桶.做这只消防桶至少需要铁皮多少平方分米?
18.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现有一个长是5cm、宽是6cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱几何体,它们的体积分别是多大?
19.10个棱长为acm的正方体摆放成如图的形状,这个图形的表面积是多少?
20.如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2,那么这根木料本来的体积是多少?
答案解析部分
1.【答案】一条线;点动成 线;圆面;线动成面;圆柱体;面动成体
【解析】【解答】解:当笔尖在纸上移动时,形成直线,这说明:点动成线;表针旋转时,形成了一个圆面,这说明:线动成面;长方形纸片绕它的一边旋转,形成的几何图形就是圆柱,这说明:面动成体。
故答案为:直线,点动成线,圆面,线动成面,圆柱,面动成体.
【分析】根据点、线、面、体的含义进行作答即可。
2.【答案】30cm
【解析】【解答】∵六棱柱有6条棱,且每条棱的长度均为5 cm,∴所有侧棱之和=6×5 cm=30 cm.故答案为:30cm
【分析】六棱柱有6条棱,由每条棱的长度,求出侧棱之和.
3.【答案】27π
【解析】【解答】直线AB为轴,将正方形旋转一周可得圆柱体,圆柱的高为3 cm,底面直径为6 cm,∴所得几何体的体积=32π 3=27π,故答案为:27π
【分析】正方形旋转一周得到的是圆柱体,正方形的边长得到圆柱的高和底面直径,求出圆柱体的体积.
4.【答案】24
【解析】【解答】解:表面积是2×2×6=24.
故答案为:24.
【分析】挖去一个棱长为1的小正方体,通过平移的方法,可以发现得到的图形与原图形表面积相等,从而利用正方体的表面积计算方法算出答案。
5.【答案】33
【解析】【解答】解:根据题意得:
第一层露出的表面积为:1×1×6﹣1×1=5;
第二层露出的表面积为:1×1×6×4﹣1×1×13=11;
第三层露出的表面积为:1×1×6×9﹣1×1×37=17.
所以红色部分的面积为:5+11+17=33.
故答案为:33
【分析】根据表面积的计算方法,分层计算出每层需要染成红色的面积,再相加即可。
6.【答案】120;164
【解析】【解答】∵两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,
∴在这个新长方体中,体积是:2×(5×4×3)=120(cm3),
表面积有以下三种情形:
①.重叠的是长.宽分别为5cm,4cm的面,
则新长方体表面积是2×(5×4)+4×(5×3)+4×(4×3)=148(cm2);
②.重叠的是长.高分别为5cm,3cm的面,
则新长方体表面积是4×(5×4)+2×(5×3)+4×(4×3)=158(cm2);
③.重叠的是宽.高分别为4cm,3cm的面,
则新长方体表面积是4×(5×4)+4×(5×3)+2×(4×3)=164(cm2).
答:在这些新长方体中,表面积最大是164cm2
【分析】两个完全相同的长方体的长.宽.高分别为5cm.4cm.3cm,把它们叠放在一起组成个新长方体,这个新长方体无论怎样叠放,其体积都不会变化,就是原一个长方体的体积乘以2;但表面积就要分三种情况来讨论:①.重叠的是长.宽分别为5cm,4cm的面,②.重叠的是长.高分别为5cm,3cm的面,③.重叠的是宽.高分别为4cm,3cm的面,然后分别按长方体的表面积就是方法算出答案,再比较大小即可得出答案。
7.【答案】A
【解析】【解答】解:正方体不能由一个平面图形绕某直线旋转一周得到,故A满足题意;
球体可以由一个圆绕一条直径旋转一周得到,故B不满足题意;
圆锥可以由一个直角三角形绕一条直角边旋转一周得到,故C不满足题意;
圆柱可以由一个长方形绕一条边旋转一周得到,故D不满足题意.
故答案为:A.
【分析】根据点动成线、线动成面、面动成体的知识进行解答.
8.【答案】B
【解析】【解答】解:直棱柱不管从哪个侧面看都是长方形.
故答案为:B.
【分析】棱柱由上下两个底面以及侧面组成,上下两个底面可以是全等的多边形,侧面是四边形;棱长与底面垂直的棱柱叫直棱柱,据此即可得出答案.
9.【答案】B
【解析】【解答】解:根据棱柱的定义可知:①是四棱柱,③是三棱柱,其余的均不是棱柱,
故棱柱有个.
故答案为:B.
【分析】有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱,据此判断.
10.【答案】B
【解析】【解答】解:A、长方体、正方体都是棱柱,不符合题意;
B、三棱柱的侧面是长方形,符合题意;
C、直六棱柱有六个侧面且侧面为长方形,不符合题意;
D、棱柱的底面都是多边形,不符合题意;
故答案为:B
【分析】根据棱柱的定义逐项判断即可。
11.【答案】B
【解析】【解答】解:沿着某一直线旋转180°后,一定能形成圆锥的是等腰三角形.
故答案为:B.
【分析】等腰三角形沿着底边上的高旋转一周可得到圆锥,据此判断.
12.【答案】C
【解析】【解答】解:黑板擦属于体,但留下的痕迹是表现在平面上而不是空间的,所以是面.
故答案为:C.
【分析】用黑板擦擦黑板时,留下的痕迹是表现在平面上的,据此判断.
13.【答案】C
【解析】【解答】当硬币在地面某位置快速旋转时,形成的几何体是球,
故答案为:C.
【分析】根据面动成体,故硬币在地面某位置旋转时,形成球体。
14.【答案】D
【解析】【解答】解:原积木所缺的几何体左视图为一个由4个棱长为1的小正方体组成的大正方体,所以可排除选项A和C;俯视图为一个由4个小正方体组成的L形,所以可排除选项B.
故答案为:D.
【分析】根据 用6个棱长为1的小正方体可以粘合形成不同形状的积木, 对每个选项一一判断即可。
15.【答案】解:∵已知三个面上的数字为4、5、7,且六个面分别标着连续的整数,∴这六个数中一定含有4、5、6、7,∴这六个数字可能为2、3、4、5、6、7;或3、4、5、6、7、8;或4、5、6、7、8、9;当这六个数为2、3、4、5、6、7时,其和为2+3+4+5+6+7=27;当这六个数为3、4、5、6、7、8时,其和为3+4+5+6+7+8=33;当这六个数为4、5、6、7、8、9时,其和为4+5+6+7+8+9=39;故答案为:27或33或39.
【解析】【分析】由于正方体的前面标注的是4,右面标注的是5,上面标注的是7,又六个面分别标着连续的整数,故这六个数中一定含有4、5、6、7,从而得出此题共有三种情况:这六个数字可能为2、3、4、5、6、7;或3、4、5、6、7、8;或4、5、6、7、8、9;然后根据有理数的加法法则分别算出其和即可。
16.【答案】解:以宽为旋转轴,V=π×52×4=100π;
以长为旋转轴,V=π×42×5=80π
【解析】【分析】根据面运动成体得出将长方形的一边旋转一周应该是一个圆柱,此题两种情况: 情况①以长为4的边旋转一周,所得圆柱的高就是4,底面圆的半径是5,根据圆柱的体积公式即可算出答案;情况②以长为5的边旋转一周,所得圆柱的高就是5,底面圆的半径是4,根据圆柱的体积公式即可算出答案;
17.【答案】解:π×4×5+π×(4÷2)2
=20π+4π
=24π(平方分米)
答:做这只消防桶至少需要铁皮24π平方分米.
【解析】【分析】由于水桶无盖,所以只求圆柱的侧面积和一个底面的面积和,根据圆柱的侧面积公式、圆的面积公式,把数据分别代入解答即可.
18.【答案】解:①绕长所在的直线旋转一周得到圆柱体积为:π×52×6=150π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×62×5=180π(cm3).
答:它们的体积分别是150π(cm3)和180π(cm3)
【解析】【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
19.【答案】解:6×6×(a×a)=36a2(cm2)
故这个图形的表面积是36a2cm2.
【解析】【分析】分别得到前后左右上下6个方向面的个数,再乘以一个面的面积即可求解.
20.【答案】3200cm3解答:∵把长方体木料锯成3段后,其表面积增加了四个截面,因此每个截面的面积为80÷4=20cm2,∴这根木料本来的体积是:1.6×100×20=3200(cm3)
【解析】【分析】根据长方体的切割特点:切割成三段后,表面积是增加了4个长方体的侧面的面积,求出这根木料的侧面积,再利用长方体的体积公式即可解答.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
