2023-2024学年 人教版八年级数学上册11.1 与三角形有关的线段 课后提升练 (含解析)
文档属性
| 名称 | 2023-2024学年 人教版八年级数学上册11.1 与三角形有关的线段 课后提升练 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 19:01:03 | ||
图片预览

文档简介
11.1 与三角形有关的线段 课后提升练
一、填空题
1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形有 个.
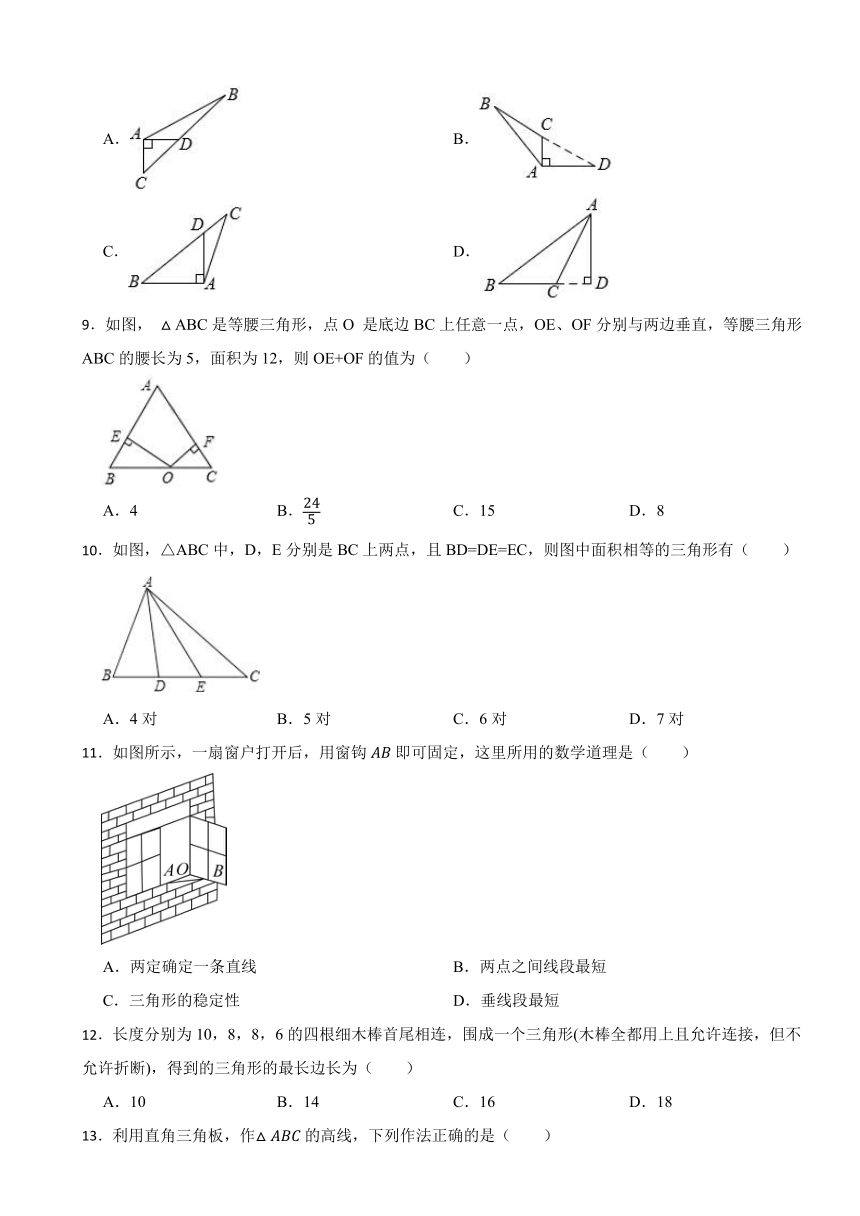
2.如图所示,三角形的两边长分别是4cm和6cm,则第三边长x的范围是
3.如图,的三条中线AD,BE,CF交于点O,若的面积为20,那么阴影部分的面积之和为 .
4.如图,是的中线,是的中线,若,则 .
5.空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的 。
二、选择题
6.三角形的两边长分别为和,此三角形第三边长可能是( )
A. B. C. D.
7.下列长度的三条线段能组成三角形的是( )
A.2,3,6 B.5,8,13 C.4,4,7 D.3,4,8
8.下列各个图形中,是的高的是( )
A. B.
C. D.
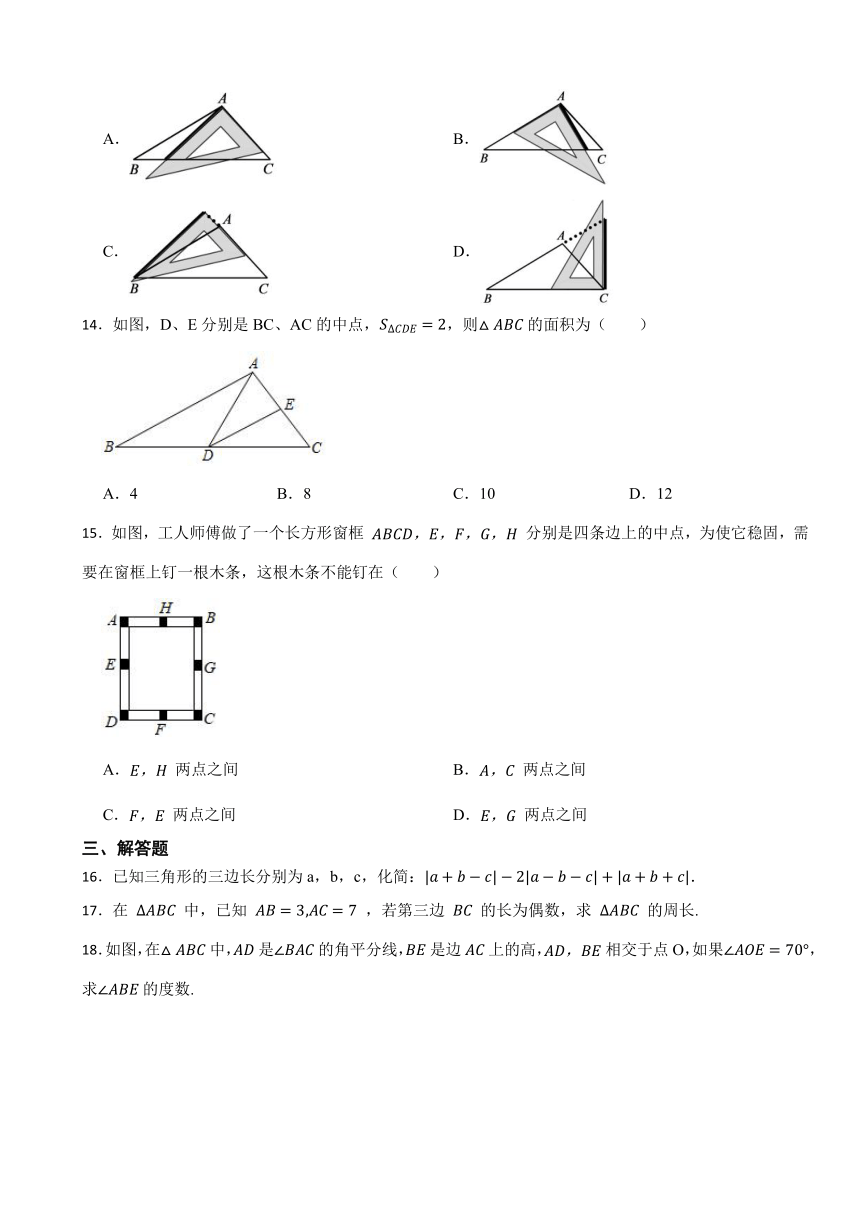
9.如图, ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )
A.4 B. C.15 D.8
10.如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
A.4对 B.5对 C.6对 D.7对
11.如图所示,一扇窗户打开后,用窗钩即可固定,这里所用的数学道理是( )
A.两定确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
12.长度分别为10,8,8,6的四根细木棒首尾相连,围成一个三角形(木棒全都用上且允许连接,但不允许折断),得到的三角形的最长边长为( )
A.10 B.14 C.16 D.18
13.利用直角三角板,作的高线,下列作法正确的是( )
A. B.
C. D.
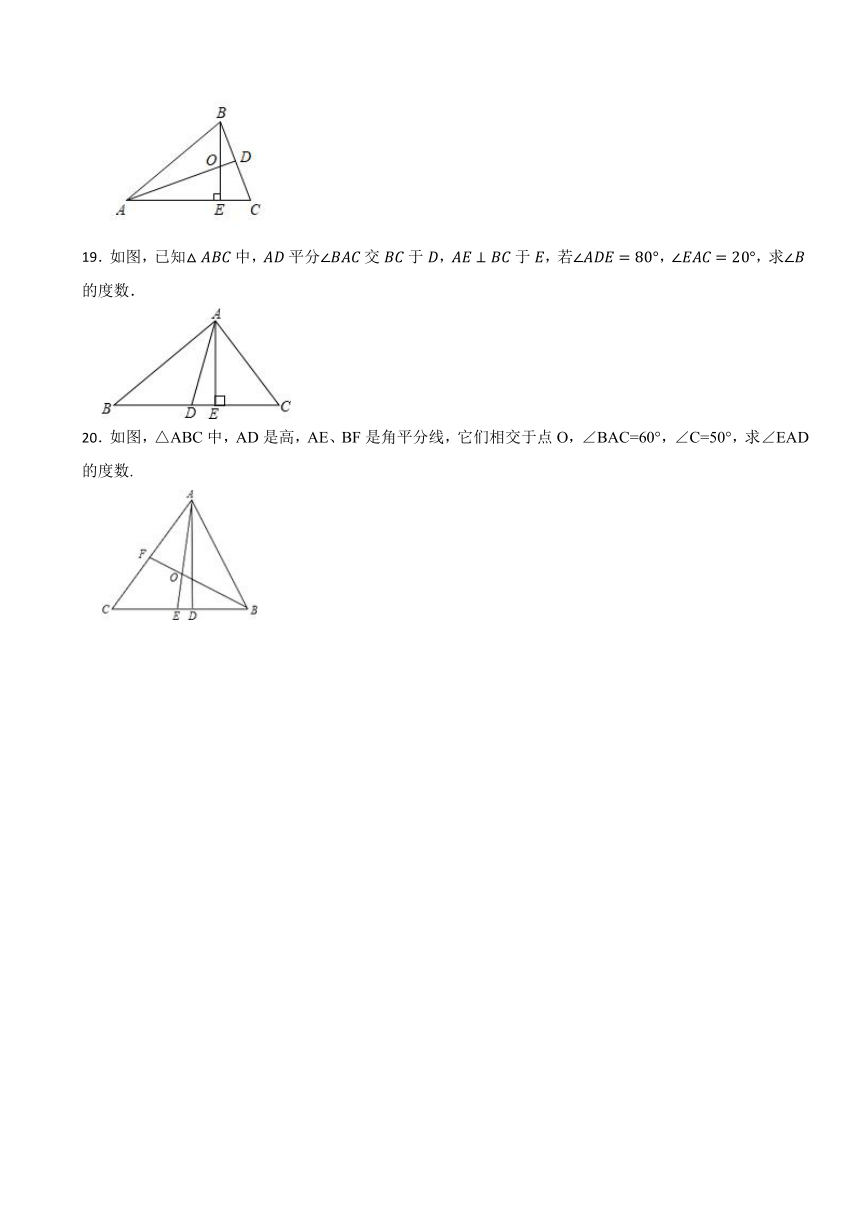
14.如图,D、E分别是BC、AC的中点,,则的面积为( )
A.4 B.8 C.10 D.12
15.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
三、解答题
16.已知三角形的三边长分别为a,b,c,化简:.
17.在 中,已知 ,若第三边 的长为偶数,求 的周长.
18.如图,在中,是的角平分线,是边上的高,相交于点O,如果,求的度数.
19.如图,已知中,平分交于,于,若,,求的度数.
20.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
答案解析部分
1.【答案】3
【解析】【解答】解:∵三角形三边长分别为2,x,13,
∴13﹣2<x<13+2,即11<x<15,
∵x为正整数,
∴x可以为12、13、14,共3个.
故答案为:3.
【分析】根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,可列出不等式组,求出第三边x的取值范围,再找出该范围内的整数个数即可得出答案.
2.【答案】
【解析】【解答】解:三角形的两边长分别为4cm和6cm,
第三边长的取值范围是:,
即:,
故答案为:.
【分析】根据三角形三边的关系可得,再求解即可。
3.【答案】10
【解析】【解答】解:,,是的中线,
,,,
阴影部分面积之和.
故答案为:10.
【分析】根据三角形中线的概念以及三角形的面积公式可得S△AOF=S△BOF,S△BOD=S△COD,S△AOE=S△COE,推出S阴影=S△ABC,据此计算.
4.【答案】12
【解析】【解答】∵ 是 的中线,
∴ ,
∵ 是 的中线,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ .
故答案为:12.
【分析】根据三角形中线的性质及等量代换可得,再结合,求出即可。
5.【答案】稳定性
【解析】【解答】解:三角形具有稳定性。
【分析】根据三角形的稳定性的应用作答即可。
6.【答案】C
【解析】【解答】解:设第三边为,由三角形三条边的关系可得:,
即,
此三角形第三边长可能是,只有C符合.
故答案为:C.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边的范围,进而判断.
7.【答案】C
【解析】【解答】解:A、∵2+3<6,∴2、3、6三条线段不能为围成三角形,故此选项不符合题意;
B、∵5+8=13,∴5、8、13三条线段不能为围成三角形,故此选项不符合题意;
C、∵4+4>7,∴4、4、7三条线段能为围成三角形,故此选项符合题意;
D、∵3+4<8,∴3、4、8三条线段不能为围成三角形,故此选项不符合题意.
故答案为:C.
【分析】由三角形三边关系,只需要判断较小两边的和是否大于最大边长即可,从而一一判断得出答案.
8.【答案】D
【解析】【解答】解:从三角形一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫三角形的高,
只有D选项符合,
故答案为:D.
【分析】根据三角形高的定义求解即可。
9.【答案】B
【解析】【解答】解:连接AO,如图,
∵AB=AC=5,
∴S△ABC=S△ABO+S△AOC= AB OE+ AC OF= OE+ OF=12,
∴OE+OF= ,
故答案为: B.
【分析】连接AO,如图,根据等腰三角形的两腰相等得出AB=AC,根据三角形面积的计算方法,由S△ABC=S△ABO+S△AOC= AB OE+ AC OF=即可算出答案。
10.【答案】A
【解析】【解答】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故答案为:A
【分析】根据等底同高的三角形的面积相等可求解。
11.【答案】C
【解析】【解答】解:一扇窗户打开后,用窗钩即可固定,形成一个三角形,
∴利用的数学道理是三角形的稳定性,
故答案为:C.
【分析】一扇窗户打开后,用窗钩可构成一个三角形,而三角形具有稳定性,所以依据是三角形的稳定性.
12.【答案】B
【解析】【解答】解:①当三边长为:10+8、6、8时,由于8+10>6+8,不能组成三角形;
②当三边长为:10+6、8、8时,由于8+8=10+6,不能组成三角形;
③当三边长为:8+8、6、10时,由于8+8=10+6,不能组成三角形;
④当三边长为:6+8、8、10时,由于10-8<6+8<8+10,能组成三角形,则最长边为14.
故答案为:B.
【分析】分四种情况:①当三边长为:10+8、6、8时,②当三边长为:10+6、8、8时,③当三边长为:8+8、6、10时,④当三边长为:6+8、8、10时,分别利用三角形的三边关系进行分析即可.
13.【答案】C
【解析】【解答】解:由三角形的高线的定义可知:
A、作法不符合题意,不符合题意;
B、作法不符合题意,不符合题意;
C、作法符合题意,符合题意;
D、作法不符合题意,不符合题意;
故答案为:C.
【分析】根据高线的定义逐项判断即可。
14.【答案】B
【解析】【解答】解:∵D、E分别是BC、AC的中点,
∴AD,DE分别为△ABC和△ADC的中线,
∴,
∴.
故答案为:B.
【分析】由题意可得AD,DE分别为△ABC和△ADC的中线,则S△ADC=2S△CDE,S△ABC=2S△ADC,据此计算.
15.【答案】D
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
16.【答案】解:由题意得:,
,
,
,
,
.
【解析】【分析】根据三角形三边的关系去掉绝对值,再合并同类项即可。
17.【答案】解: 在 中, ,
第三边 的取值范围是:
符合条件的偶数是 或 ,
当 时, 的周长为: ;
当 时, 的周长为: .
的周长为 或 .
【解析】【分析】根据三角形的三边关系可得由BC的长为偶数,求出BC的长,从而求出三角形的周长.
18.【答案】解:∵是边上的高,
∴.
∴.
∵是的角平分线,
∴.
∴.
【解析】【分析】根据高线的概念可得∠AEB=90°,则∠OAE=90°-∠AOE=20°,由角平分线的概念可得∠BAC=2∠OAE=40°,然后根据∠ABE=90°-∠BAC进行计算.
19.【答案】解:,,
,
.
,
.
【解析】【分析】利用三角形的内角和求出,,再利用三角形外角的性质可得,最后求出即可。
20.【答案】解:∵∠BAC=60°,∠C=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-90°-∠C=40°,
∵AE是角平分线,
∴∠EAC=30°
∴∠EAD=∠DAC-∠EAC=40°-30°=10°
【解析】【分析】先由AD是高得到 ∠ADC=90° ,接着通过三角形内角和求到∠DAC=40°,再由AE是角平分线得到 ∠EAC=30° ,最后由 ∠EAD=∠DAC-∠EAC 算出∠EAD的度数.
一、填空题
1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形有 个.
2.如图所示,三角形的两边长分别是4cm和6cm,则第三边长x的范围是
3.如图,的三条中线AD,BE,CF交于点O,若的面积为20,那么阴影部分的面积之和为 .
4.如图,是的中线,是的中线,若,则 .
5.空调外机安装在墙壁上时,一般都会像如图所示的方法固定在墙壁上,这种方法是利用了三角形的 。
二、选择题
6.三角形的两边长分别为和,此三角形第三边长可能是( )
A. B. C. D.
7.下列长度的三条线段能组成三角形的是( )
A.2,3,6 B.5,8,13 C.4,4,7 D.3,4,8
8.下列各个图形中,是的高的是( )
A. B.
C. D.
9.如图, ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )
A.4 B. C.15 D.8
10.如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
A.4对 B.5对 C.6对 D.7对
11.如图所示,一扇窗户打开后,用窗钩即可固定,这里所用的数学道理是( )
A.两定确定一条直线 B.两点之间线段最短
C.三角形的稳定性 D.垂线段最短
12.长度分别为10,8,8,6的四根细木棒首尾相连,围成一个三角形(木棒全都用上且允许连接,但不允许折断),得到的三角形的最长边长为( )
A.10 B.14 C.16 D.18
13.利用直角三角板,作的高线,下列作法正确的是( )
A. B.
C. D.
14.如图,D、E分别是BC、AC的中点,,则的面积为( )
A.4 B.8 C.10 D.12
15.如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
三、解答题
16.已知三角形的三边长分别为a,b,c,化简:.
17.在 中,已知 ,若第三边 的长为偶数,求 的周长.
18.如图,在中,是的角平分线,是边上的高,相交于点O,如果,求的度数.
19.如图,已知中,平分交于,于,若,,求的度数.
20.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠EAD的度数.
答案解析部分
1.【答案】3
【解析】【解答】解:∵三角形三边长分别为2,x,13,
∴13﹣2<x<13+2,即11<x<15,
∵x为正整数,
∴x可以为12、13、14,共3个.
故答案为:3.
【分析】根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边,可列出不等式组,求出第三边x的取值范围,再找出该范围内的整数个数即可得出答案.
2.【答案】
【解析】【解答】解:三角形的两边长分别为4cm和6cm,
第三边长的取值范围是:,
即:,
故答案为:.
【分析】根据三角形三边的关系可得,再求解即可。
3.【答案】10
【解析】【解答】解:,,是的中线,
,,,
阴影部分面积之和.
故答案为:10.
【分析】根据三角形中线的概念以及三角形的面积公式可得S△AOF=S△BOF,S△BOD=S△COD,S△AOE=S△COE,推出S阴影=S△ABC,据此计算.
4.【答案】12
【解析】【解答】∵ 是 的中线,
∴ ,
∵ 是 的中线,
∴ ,
∴ ,
又∵ ,
∴ ,
∴ .
故答案为:12.
【分析】根据三角形中线的性质及等量代换可得,再结合,求出即可。
5.【答案】稳定性
【解析】【解答】解:三角形具有稳定性。
【分析】根据三角形的稳定性的应用作答即可。
6.【答案】C
【解析】【解答】解:设第三边为,由三角形三条边的关系可得:,
即,
此三角形第三边长可能是,只有C符合.
故答案为:C.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边的范围,进而判断.
7.【答案】C
【解析】【解答】解:A、∵2+3<6,∴2、3、6三条线段不能为围成三角形,故此选项不符合题意;
B、∵5+8=13,∴5、8、13三条线段不能为围成三角形,故此选项不符合题意;
C、∵4+4>7,∴4、4、7三条线段能为围成三角形,故此选项符合题意;
D、∵3+4<8,∴3、4、8三条线段不能为围成三角形,故此选项不符合题意.
故答案为:C.
【分析】由三角形三边关系,只需要判断较小两边的和是否大于最大边长即可,从而一一判断得出答案.
8.【答案】D
【解析】【解答】解:从三角形一个顶点向它的对边所在直线画垂线,顶点和垂足间的线段叫三角形的高,
只有D选项符合,
故答案为:D.
【分析】根据三角形高的定义求解即可。
9.【答案】B
【解析】【解答】解:连接AO,如图,
∵AB=AC=5,
∴S△ABC=S△ABO+S△AOC= AB OE+ AC OF= OE+ OF=12,
∴OE+OF= ,
故答案为: B.
【分析】连接AO,如图,根据等腰三角形的两腰相等得出AB=AC,根据三角形面积的计算方法,由S△ABC=S△ABO+S△AOC= AB OE+ AC OF=即可算出答案。
10.【答案】A
【解析】【解答】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故答案为:A
【分析】根据等底同高的三角形的面积相等可求解。
11.【答案】C
【解析】【解答】解:一扇窗户打开后,用窗钩即可固定,形成一个三角形,
∴利用的数学道理是三角形的稳定性,
故答案为:C.
【分析】一扇窗户打开后,用窗钩可构成一个三角形,而三角形具有稳定性,所以依据是三角形的稳定性.
12.【答案】B
【解析】【解答】解:①当三边长为:10+8、6、8时,由于8+10>6+8,不能组成三角形;
②当三边长为:10+6、8、8时,由于8+8=10+6,不能组成三角形;
③当三边长为:8+8、6、10时,由于8+8=10+6,不能组成三角形;
④当三边长为:6+8、8、10时,由于10-8<6+8<8+10,能组成三角形,则最长边为14.
故答案为:B.
【分析】分四种情况:①当三边长为:10+8、6、8时,②当三边长为:10+6、8、8时,③当三边长为:8+8、6、10时,④当三边长为:6+8、8、10时,分别利用三角形的三边关系进行分析即可.
13.【答案】C
【解析】【解答】解:由三角形的高线的定义可知:
A、作法不符合题意,不符合题意;
B、作法不符合题意,不符合题意;
C、作法符合题意,符合题意;
D、作法不符合题意,不符合题意;
故答案为:C.
【分析】根据高线的定义逐项判断即可。
14.【答案】B
【解析】【解答】解:∵D、E分别是BC、AC的中点,
∴AD,DE分别为△ABC和△ADC的中线,
∴,
∴.
故答案为:B.
【分析】由题意可得AD,DE分别为△ABC和△ADC的中线,则S△ADC=2S△CDE,S△ABC=2S△ADC,据此计算.
15.【答案】D
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
16.【答案】解:由题意得:,
,
,
,
,
.
【解析】【分析】根据三角形三边的关系去掉绝对值,再合并同类项即可。
17.【答案】解: 在 中, ,
第三边 的取值范围是:
符合条件的偶数是 或 ,
当 时, 的周长为: ;
当 时, 的周长为: .
的周长为 或 .
【解析】【分析】根据三角形的三边关系可得由BC的长为偶数,求出BC的长,从而求出三角形的周长.
18.【答案】解:∵是边上的高,
∴.
∴.
∵是的角平分线,
∴.
∴.
【解析】【分析】根据高线的概念可得∠AEB=90°,则∠OAE=90°-∠AOE=20°,由角平分线的概念可得∠BAC=2∠OAE=40°,然后根据∠ABE=90°-∠BAC进行计算.
19.【答案】解:,,
,
.
,
.
【解析】【分析】利用三角形的内角和求出,,再利用三角形外角的性质可得,最后求出即可。
20.【答案】解:∵∠BAC=60°,∠C=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-90°-∠C=40°,
∵AE是角平分线,
∴∠EAC=30°
∴∠EAD=∠DAC-∠EAC=40°-30°=10°
【解析】【分析】先由AD是高得到 ∠ADC=90° ,接着通过三角形内角和求到∠DAC=40°,再由AE是角平分线得到 ∠EAC=30° ,最后由 ∠EAD=∠DAC-∠EAC 算出∠EAD的度数.
