2023-2024学年 人教版八年级数学上册11.2 与三角形有关的角 课后提升练(含解析)
文档属性
| 名称 | 2023-2024学年 人教版八年级数学上册11.2 与三角形有关的角 课后提升练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 372.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 00:00:00 | ||
图片预览

文档简介
11.2 与三角形有关的角 课后提升练 2023-2024学年度人教版八年级数学上册
一、选择题
1.一个三角形三个内角的度数之比为,则这个三角形一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
2.等腰三角形有一个角是,则这个等腰三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.已知中,,则的角度可能是( )
A. B. C. D.
4.在中,,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
5.体育课上的侧压腿动作(图1)可以抽象为几何图形(图2),如果,则等于( )
A. B. C. D.
6.如图,AD与BC相交于点O,AB∥CD,如果 ∠B=20°,∠D=40° ,那么∠AOC的度数为( )
A.80° B.60° C.40° D.20°
7.如图,将含有30°角的直角三角尺的直角顶点与一张长方形纸片的顶点重合,其中一个锐角顶点在一边上.若,则的度数是( )
A.15° B.25° C.30° D.35°
8.如果一个三角形的两个内角分别为和,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
9.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
10.如图,直线a∥b,若∠1=24°,∠2=70°,则∠A等于( )
A.46° B.45° C.40° D.30°
二、填空题
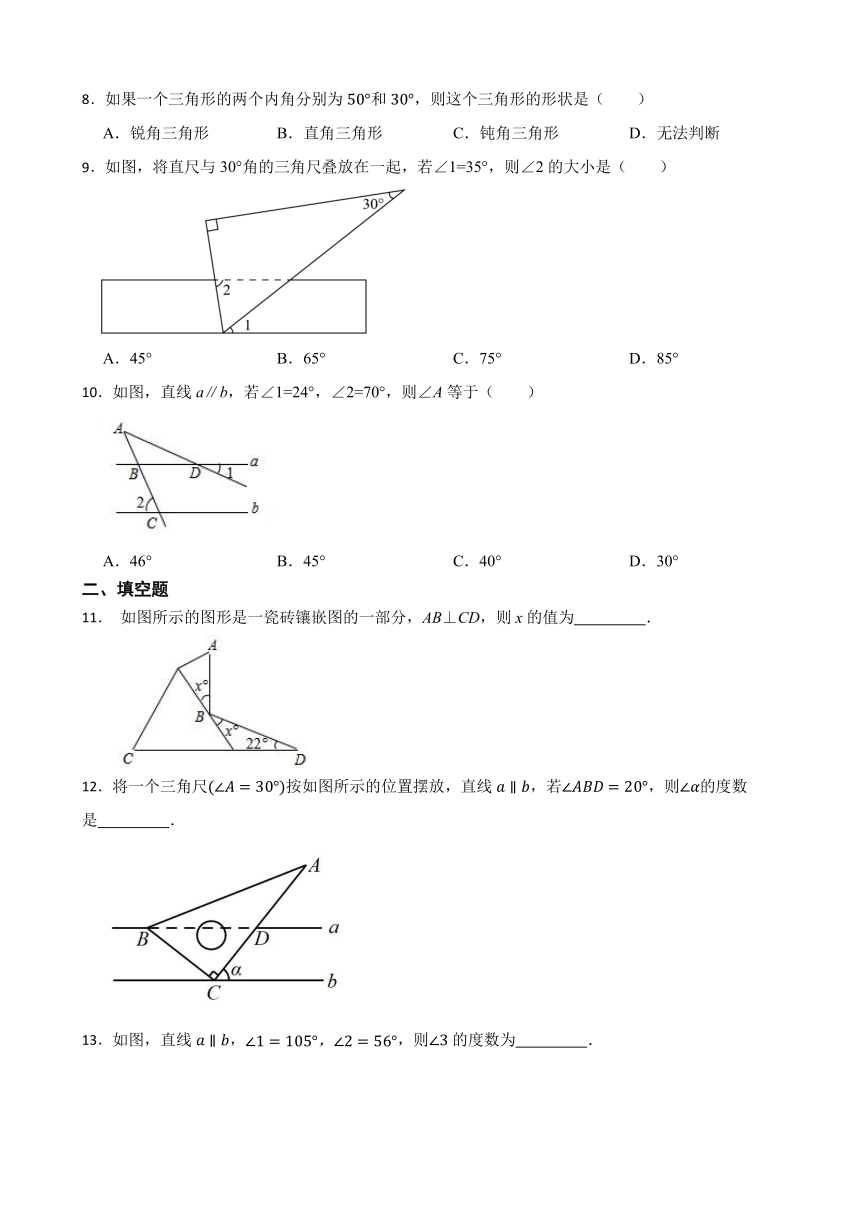
11. 如图所示的图形是一瓷砖镶嵌图的一部分,AB⊥CD,则x的值为 .
12.将一个三角尺按如图所示的位置摆放,直线,若,则的度数是 .
13.如图,直线,,则的度数为 .
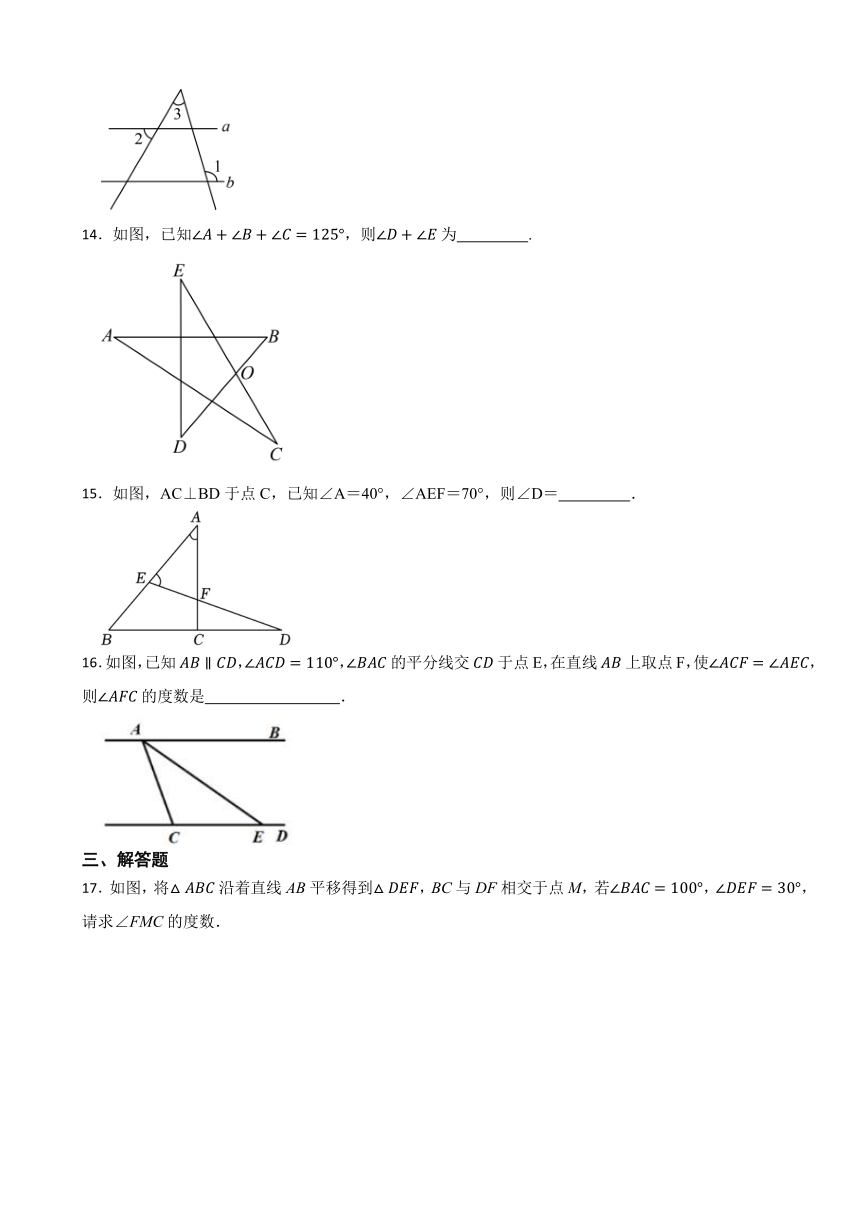
14.如图,已知,则为 .
15.如图,AC⊥BD于点C,已知∠A=40°,∠AEF=70°,则∠D= .
16.如图,已知,,的平分线交于点E,在直线上取点F,使,则的度数是 .
三、解答题
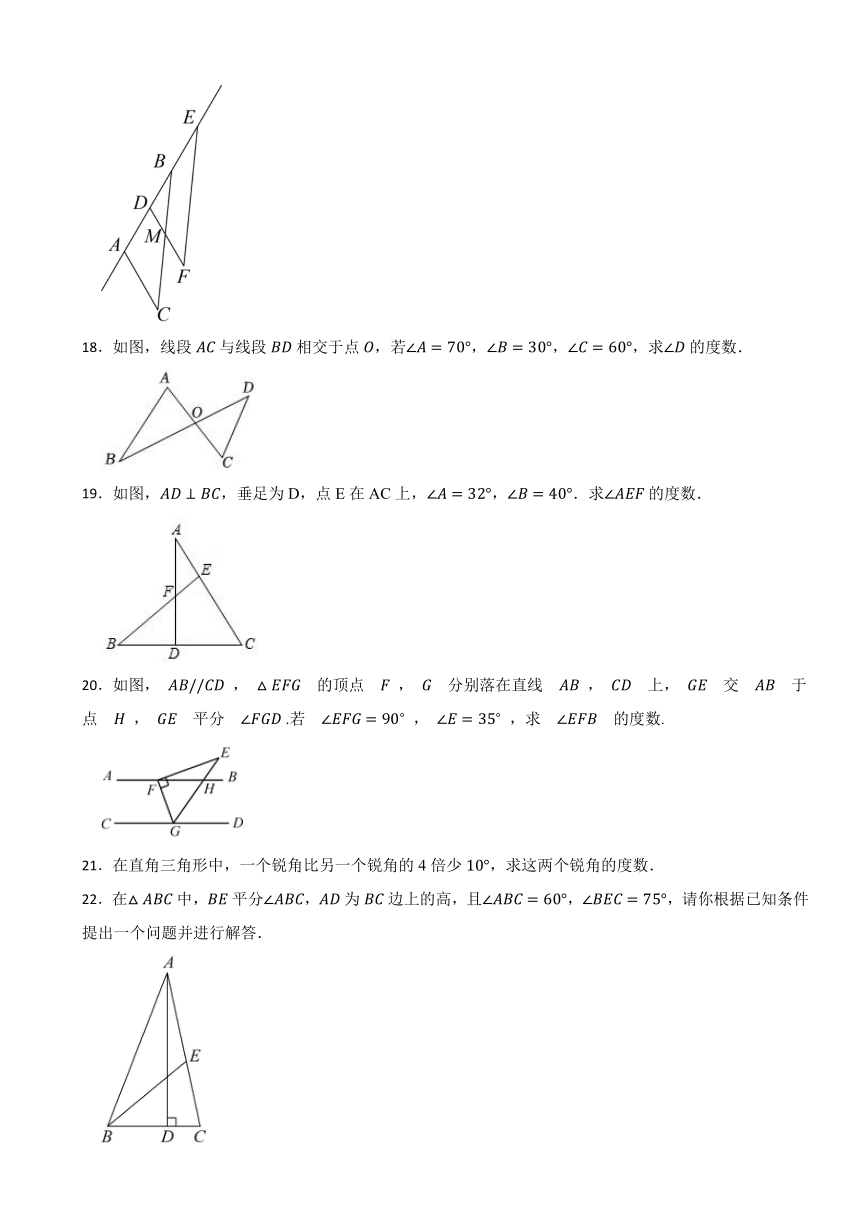
17.如图,将沿着直线AB平移得到,BC与DF相交于点M,若,,请求∠FMC的度数.
18.如图,线段与线段相交于点,若,,,求的度数.
19.如图,,垂足为D,点E在AC上,,.求的度数.
20.如图, , 的顶点 , 分别落在直线 , 上, 交 于点 , 平分 .若 , ,求 的度数.
21.在直角三角形中,一个锐角比另一个锐角的4倍少,求这两个锐角的度数.
22.在中,平分,为边上的高,且,,请你根据已知条件提出一个问题并进行解答.
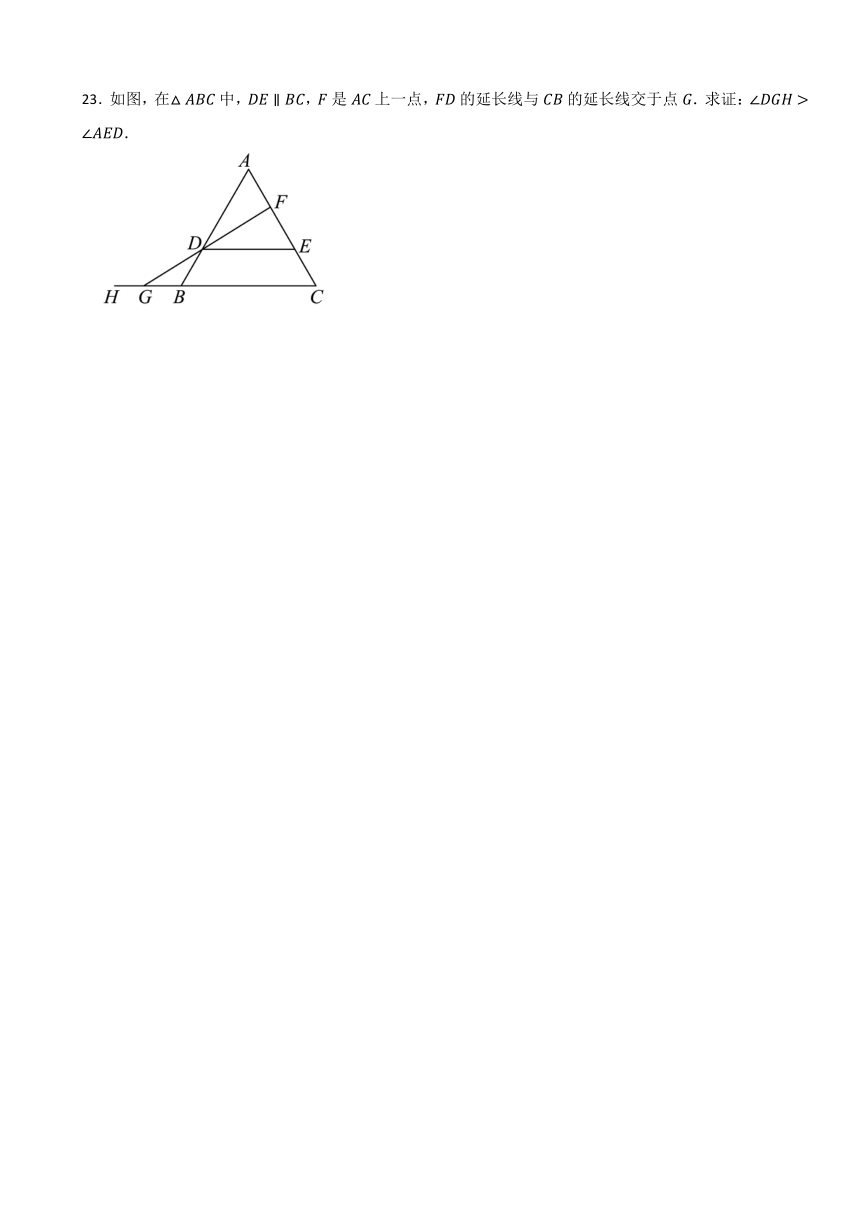
23.如图,在中,,是上一点,的延长线与的延长线交于点.求证:.
答案解析部分
1.【答案】D
【解析】【解答】解:三个角的角度分别为:,,,
故这个角一定是钝角三角形.
故答案为:D.
【分析】考查三角形的内角和为180°,利用三角形三个内角的度数之比,求出每个角的度数,就能求出这个三角形.
2.【答案】A
【解析】【解答】解:∵三角形是等腰三角形,∴当80°是顶角时,则底角为(180°-80°)÷2=50°,此时三角形为锐角三角形;当80°为底角时,则顶角为180°-80°-80°=20°,此时三角形仍是锐角三角形.
故答案为:A.
【分析】由等腰三角形的定义可知,其中有两个底角相等,再由三角形的内角和定理,就可以计算出其它的角的大小,从而判断三角形的类型.
3.【答案】A
【解析】【解答】解:∵△ABC中,∠A=90°,
∴∠B+∠C=90°,
∴∠C为锐角,可能为80°.
故答案为:A.
【分析】由内角和定理可得∠B+∠C=90°,据此判断.
4.【答案】B
【解析】【解答】解:∵,,
∴,
故是直角三角形.
故答案为:B.
【分析】根据直角三角形的判定即可求解.
5.【答案】B
【解析】【解答】解:由题意得∠1=∠2+90°,
∴∠2=20°,
故答案为:B
【分析】根据三角形外角的性质结合题意即可求解。
6.【答案】B
【解析】【解答】解:∵AB//CD,
∴∠C=∠B=20°,
又∵∠D=40°,
∴∠AOC=∠C+∠D=60°,
故答案为:B.
【分析】根据平行线的性质求出∠C=∠B=20°,再根据三角形的外角计算求解即可。
7.【答案】B
【解析】【解答】解:如图,∵AB∥CD,∠1=55°,
∴∠3=∠1=55°,
∵∠3=∠2+30°,
∴∠2=∠3-30°=55°-30°=25°;
故答案为:B.
【分析】由平行线的性质可得∠3=∠1=55°,利用三角形外角的性质可得∠3=∠2+30°,据此即可求解.
8.【答案】C
【解析】【解答】∵一个三角形的两个内角分别为和,
∴第三个内角为:180°-50°-30°=100°,
∴三角形为钝角三角形,
故答案为:C.
【分析】先利用三角形的内角和求出第三个角的度数,再判断三角形的形状即可.
9.【答案】D
【解析】【解答】解:如图,
,
,
,,
.
故答案为:D.
【分析】由30°的直角三角形可知∠3=60°,再利用二直线平行,同旁内角互补求得∠2的度数.
10.【答案】A
【解析】【解答】解: ∵∠1=24°,
∴∠ADB=∠1=24°.
∵直线a∥b,∠2=70°,
∴∠DBC=∠2=70°.
∵∠BDC是△ABD的外角,
∴∠A=∠DBC-∠ADB=70°-24°=46°.
故答案为:A.
【分析】先根据对顶角相等得出∠ADB的度数,再由平行线的性质求出∠DBC的度数,由三角形外角的性质即可得出结论.
11.【答案】34
【解析】【解答】解:如图,
∵AB⊥CD,
∴∠BED=90°,
∵∠ABG与∠EBF互为对顶角,
∴∠ABG=∠EBF=x°,
在△BED中,∠EBD+∠D+∠BED=180°,
即x°+x°+22°+90°=180°,
解得:x°=34°,
故答案为:34.
【分析】根据对顶角的性质和三角形内角和定理列式求解即可得到答案.
12.【答案】50°
【解析】【解答】解:如图,
∵∠A=30°,∠ACB=90°,
∴∠ABC=180°-∠A-∠ACB=60°,
又∵∠ABD=20°,
∴∠1=∠ABC-∠ABD=40°,
∵a∥b,
∴∠2=∠1=40°,
∴ =180°-∠2-∠ACB=180°-90°-40°=50°.
故答案为:50°.
【分析】由三角形的内角和定理算出∠ABC=60°,由角的和差算出∠1=40°,根据二直线平行,内错角相等得∠2=40°,最后根据平角定义算出答案.
13.【答案】
14.【答案】
15.【答案】20°
【解析】【解答】解:∵∠A=40°,∠AEF=70°,
∴∠AFD=∠A+∠AEF=110°,
又∵AC⊥BD,
∴∠ACD=90°,
∴∠D=∠AFD-∠ACD=20°,
故答案为:20°.
【分析】根据题意先求出∠AFD=∠A+∠AEF=110°,再求出∠ACD=90°,最后计算求解即可。
16.【答案】或
【解析】【解答】解:∵ AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠AEC=∠CAE,
在△ACE中,∠ACE=110°,
∴∠CAE===35°,
∴∠AEC=∠CAE=∠BAE=35°,
下面分二种情况探讨
图1图2
如图1,点F位于点A的右侧,
∵∠ACF=∠AEC=35°,
∴∠AFC=180°-∠BAE-∠CAE-∠ACF=180°-35°×3=75°,
如图2,点F位于点A的左侧,
∵∠ACF=∠AEC=35°,
∴∠AFC=∠BAC-∠ACF=∠BAE+∠CAE-∠ACF=35°+35-35°=35°.
故答案为:35°或75°.
【分析】由平行线性质得∠BAE=∠AEC,再由角平分线的性质得∠BAE=∠CAE,等量代换得∠AEC=∠CAE=∠BAE=35°,点F作为一个动点分两种情况进行讨论,分别为A点的左侧与右侧,画出图形,并结合图形由三角形的外角定理及内角和定理解决.
17.【答案】解:由平移可知,,
∴,
∵DF∥AC,
∴.
【解析】【分析】根据平移的性质求出 ,, 再利用三角形的内角和定理求出∠C=50°,最后根据平行线的性质计算求解即可。
18.【答案】解:∵ ,
∴ ,
∵ , , ,
∴ ,
∴ .
【解析】【分析】根据三角形的内角和可得,再将数据代入可得,最后求出即可。
19.【答案】解:∵,
∴∠ADC=90°,
∴∠C=90°-∠A=58°,
∵.
∴=∠B+∠C=58°+40°=98°.
【解析】【分析】先利用三角形的内角和求出∠C的度数,再利用三角形外角的性质可得∠AEF的度数。
20.【答案】解:∵∠EFG=90°,∠E=35°,
∴∠FGH=55°,
∵GE平分∠FGD,AB∥CD,
∴∠FHG=∠HGD=∠FGH=55°,
∵∠FHG是△EFH的外角,
∴∠EFB=55°-35°=20°.
【解析】【点评】用三角形内角和定理可求得∠FGH的度数,由角平分线定义和平行线的性质可得 ∠FHG=∠HGD=∠FGH,再根据三角形的一个外角等于和它不相邻的内角的和可求解.
21.【答案】解:设较小的角为,则较大的角为,由题意可列:
,解得,
较大的锐角为,所以这两个角分别是和.
【解析】【分析】 设较小的角为,则较大的角为, 根据“ 一个锐角比另一个锐角的4倍少 ”列出方程,再求解即可.
22.【答案】解:提问:求的度数.
平分∠ABC,且,
,
又,
23.【答案】证明:∵是的一个外角,
∴,
∵是的一个外角,
∴,
∴,
∵,
∴,
∴.
【解析】【分析】运用平行线的性质得出∠AED=∠C,再根据外角的性质判断∠DGH>∠DBG>∠C即可。
一、选择题
1.一个三角形三个内角的度数之比为,则这个三角形一定是( )
A.等腰三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
2.等腰三角形有一个角是,则这个等腰三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.已知中,,则的角度可能是( )
A. B. C. D.
4.在中,,则的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
5.体育课上的侧压腿动作(图1)可以抽象为几何图形(图2),如果,则等于( )
A. B. C. D.
6.如图,AD与BC相交于点O,AB∥CD,如果 ∠B=20°,∠D=40° ,那么∠AOC的度数为( )
A.80° B.60° C.40° D.20°
7.如图,将含有30°角的直角三角尺的直角顶点与一张长方形纸片的顶点重合,其中一个锐角顶点在一边上.若,则的度数是( )
A.15° B.25° C.30° D.35°
8.如果一个三角形的两个内角分别为和,则这个三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
9.如图,将直尺与30°角的三角尺叠放在一起,若∠1=35°,则∠2的大小是( )
A.45° B.65° C.75° D.85°
10.如图,直线a∥b,若∠1=24°,∠2=70°,则∠A等于( )
A.46° B.45° C.40° D.30°
二、填空题
11. 如图所示的图形是一瓷砖镶嵌图的一部分,AB⊥CD,则x的值为 .
12.将一个三角尺按如图所示的位置摆放,直线,若,则的度数是 .
13.如图,直线,,则的度数为 .
14.如图,已知,则为 .
15.如图,AC⊥BD于点C,已知∠A=40°,∠AEF=70°,则∠D= .
16.如图,已知,,的平分线交于点E,在直线上取点F,使,则的度数是 .
三、解答题
17.如图,将沿着直线AB平移得到,BC与DF相交于点M,若,,请求∠FMC的度数.
18.如图,线段与线段相交于点,若,,,求的度数.
19.如图,,垂足为D,点E在AC上,,.求的度数.
20.如图, , 的顶点 , 分别落在直线 , 上, 交 于点 , 平分 .若 , ,求 的度数.
21.在直角三角形中,一个锐角比另一个锐角的4倍少,求这两个锐角的度数.
22.在中,平分,为边上的高,且,,请你根据已知条件提出一个问题并进行解答.
23.如图,在中,,是上一点,的延长线与的延长线交于点.求证:.
答案解析部分
1.【答案】D
【解析】【解答】解:三个角的角度分别为:,,,
故这个角一定是钝角三角形.
故答案为:D.
【分析】考查三角形的内角和为180°,利用三角形三个内角的度数之比,求出每个角的度数,就能求出这个三角形.
2.【答案】A
【解析】【解答】解:∵三角形是等腰三角形,∴当80°是顶角时,则底角为(180°-80°)÷2=50°,此时三角形为锐角三角形;当80°为底角时,则顶角为180°-80°-80°=20°,此时三角形仍是锐角三角形.
故答案为:A.
【分析】由等腰三角形的定义可知,其中有两个底角相等,再由三角形的内角和定理,就可以计算出其它的角的大小,从而判断三角形的类型.
3.【答案】A
【解析】【解答】解:∵△ABC中,∠A=90°,
∴∠B+∠C=90°,
∴∠C为锐角,可能为80°.
故答案为:A.
【分析】由内角和定理可得∠B+∠C=90°,据此判断.
4.【答案】B
【解析】【解答】解:∵,,
∴,
故是直角三角形.
故答案为:B.
【分析】根据直角三角形的判定即可求解.
5.【答案】B
【解析】【解答】解:由题意得∠1=∠2+90°,
∴∠2=20°,
故答案为:B
【分析】根据三角形外角的性质结合题意即可求解。
6.【答案】B
【解析】【解答】解:∵AB//CD,
∴∠C=∠B=20°,
又∵∠D=40°,
∴∠AOC=∠C+∠D=60°,
故答案为:B.
【分析】根据平行线的性质求出∠C=∠B=20°,再根据三角形的外角计算求解即可。
7.【答案】B
【解析】【解答】解:如图,∵AB∥CD,∠1=55°,
∴∠3=∠1=55°,
∵∠3=∠2+30°,
∴∠2=∠3-30°=55°-30°=25°;
故答案为:B.
【分析】由平行线的性质可得∠3=∠1=55°,利用三角形外角的性质可得∠3=∠2+30°,据此即可求解.
8.【答案】C
【解析】【解答】∵一个三角形的两个内角分别为和,
∴第三个内角为:180°-50°-30°=100°,
∴三角形为钝角三角形,
故答案为:C.
【分析】先利用三角形的内角和求出第三个角的度数,再判断三角形的形状即可.
9.【答案】D
【解析】【解答】解:如图,
,
,
,,
.
故答案为:D.
【分析】由30°的直角三角形可知∠3=60°,再利用二直线平行,同旁内角互补求得∠2的度数.
10.【答案】A
【解析】【解答】解: ∵∠1=24°,
∴∠ADB=∠1=24°.
∵直线a∥b,∠2=70°,
∴∠DBC=∠2=70°.
∵∠BDC是△ABD的外角,
∴∠A=∠DBC-∠ADB=70°-24°=46°.
故答案为:A.
【分析】先根据对顶角相等得出∠ADB的度数,再由平行线的性质求出∠DBC的度数,由三角形外角的性质即可得出结论.
11.【答案】34
【解析】【解答】解:如图,
∵AB⊥CD,
∴∠BED=90°,
∵∠ABG与∠EBF互为对顶角,
∴∠ABG=∠EBF=x°,
在△BED中,∠EBD+∠D+∠BED=180°,
即x°+x°+22°+90°=180°,
解得:x°=34°,
故答案为:34.
【分析】根据对顶角的性质和三角形内角和定理列式求解即可得到答案.
12.【答案】50°
【解析】【解答】解:如图,
∵∠A=30°,∠ACB=90°,
∴∠ABC=180°-∠A-∠ACB=60°,
又∵∠ABD=20°,
∴∠1=∠ABC-∠ABD=40°,
∵a∥b,
∴∠2=∠1=40°,
∴ =180°-∠2-∠ACB=180°-90°-40°=50°.
故答案为:50°.
【分析】由三角形的内角和定理算出∠ABC=60°,由角的和差算出∠1=40°,根据二直线平行,内错角相等得∠2=40°,最后根据平角定义算出答案.
13.【答案】
14.【答案】
15.【答案】20°
【解析】【解答】解:∵∠A=40°,∠AEF=70°,
∴∠AFD=∠A+∠AEF=110°,
又∵AC⊥BD,
∴∠ACD=90°,
∴∠D=∠AFD-∠ACD=20°,
故答案为:20°.
【分析】根据题意先求出∠AFD=∠A+∠AEF=110°,再求出∠ACD=90°,最后计算求解即可。
16.【答案】或
【解析】【解答】解:∵ AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠AEC=∠CAE,
在△ACE中,∠ACE=110°,
∴∠CAE===35°,
∴∠AEC=∠CAE=∠BAE=35°,
下面分二种情况探讨
图1图2
如图1,点F位于点A的右侧,
∵∠ACF=∠AEC=35°,
∴∠AFC=180°-∠BAE-∠CAE-∠ACF=180°-35°×3=75°,
如图2,点F位于点A的左侧,
∵∠ACF=∠AEC=35°,
∴∠AFC=∠BAC-∠ACF=∠BAE+∠CAE-∠ACF=35°+35-35°=35°.
故答案为:35°或75°.
【分析】由平行线性质得∠BAE=∠AEC,再由角平分线的性质得∠BAE=∠CAE,等量代换得∠AEC=∠CAE=∠BAE=35°,点F作为一个动点分两种情况进行讨论,分别为A点的左侧与右侧,画出图形,并结合图形由三角形的外角定理及内角和定理解决.
17.【答案】解:由平移可知,,
∴,
∵DF∥AC,
∴.
【解析】【分析】根据平移的性质求出 ,, 再利用三角形的内角和定理求出∠C=50°,最后根据平行线的性质计算求解即可。
18.【答案】解:∵ ,
∴ ,
∵ , , ,
∴ ,
∴ .
【解析】【分析】根据三角形的内角和可得,再将数据代入可得,最后求出即可。
19.【答案】解:∵,
∴∠ADC=90°,
∴∠C=90°-∠A=58°,
∵.
∴=∠B+∠C=58°+40°=98°.
【解析】【分析】先利用三角形的内角和求出∠C的度数,再利用三角形外角的性质可得∠AEF的度数。
20.【答案】解:∵∠EFG=90°,∠E=35°,
∴∠FGH=55°,
∵GE平分∠FGD,AB∥CD,
∴∠FHG=∠HGD=∠FGH=55°,
∵∠FHG是△EFH的外角,
∴∠EFB=55°-35°=20°.
【解析】【点评】用三角形内角和定理可求得∠FGH的度数,由角平分线定义和平行线的性质可得 ∠FHG=∠HGD=∠FGH,再根据三角形的一个外角等于和它不相邻的内角的和可求解.
21.【答案】解:设较小的角为,则较大的角为,由题意可列:
,解得,
较大的锐角为,所以这两个角分别是和.
【解析】【分析】 设较小的角为,则较大的角为, 根据“ 一个锐角比另一个锐角的4倍少 ”列出方程,再求解即可.
22.【答案】解:提问:求的度数.
平分∠ABC,且,
,
又,
23.【答案】证明:∵是的一个外角,
∴,
∵是的一个外角,
∴,
∴,
∵,
∴,
∴.
【解析】【分析】运用平行线的性质得出∠AED=∠C,再根据外角的性质判断∠DGH>∠DBG>∠C即可。
