12.3角的平分线的性质 同步测试题(含解析)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 12.3角的平分线的性质 同步测试题(含解析)2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 596.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 00:00:00 | ||
图片预览


文档简介
2023-2024学年人教版八年级数学上册《12.3角平分线的性质》同步测试题(附答案)
一、单选题(满分32分)
1.如图,为促进某地旅游业的发展,当地旅游部门要在三条公路AB,AC,BC两两相交后围成的三角形区域内修建一个度假村,若这个度假村到三条公路的距离相等,则度假村应建在( )
A.三边的垂直平分线的交点上 B.三条角平分线的交点上
C.三条高线的交点上 D.三边中线的交点上
2.如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )
A.PC=PD B.OC=OD C.OC=OP D.∠CPO=∠DPO
3.如图,已知在四边形中,,平分,,,,则四边形的面积是( )
A.40 B.42 C.46 D.48
4.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.2 B.3 C.4 D.5
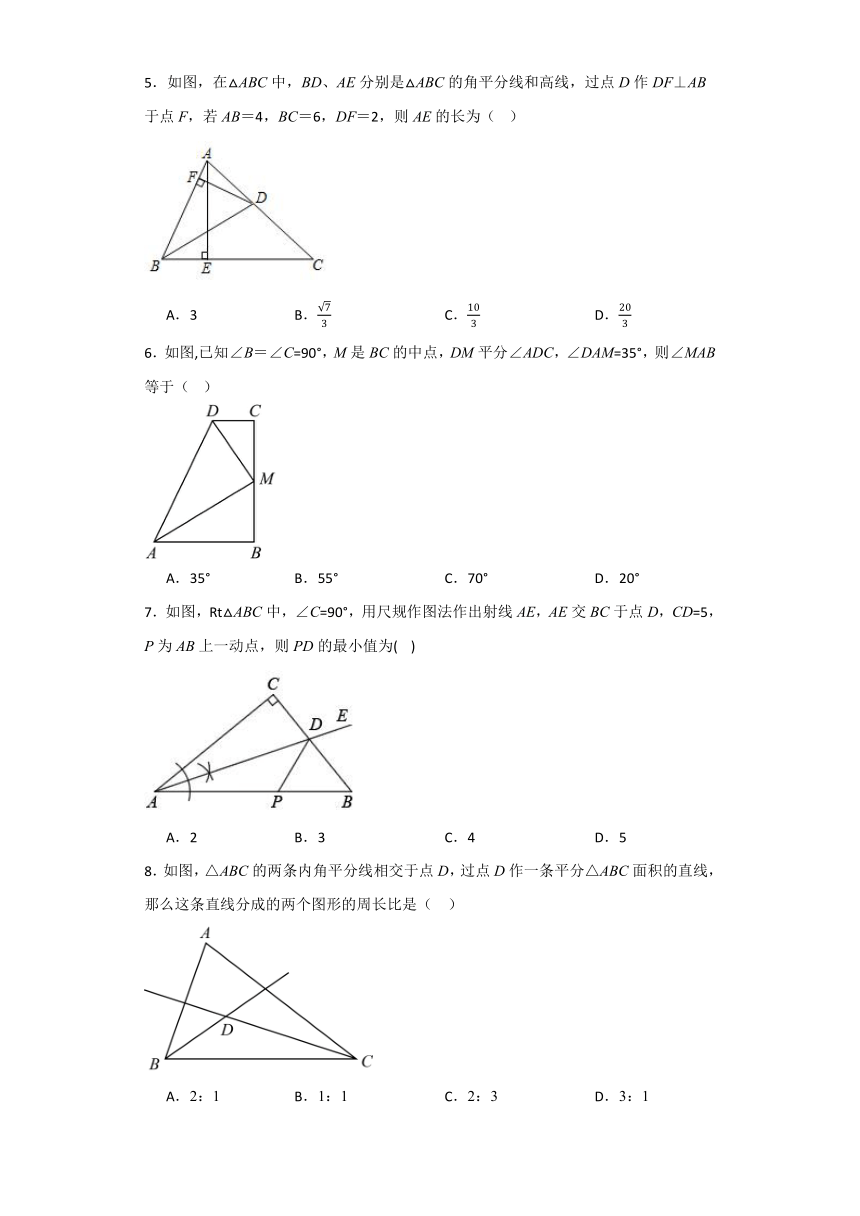
5.如图,在△ABC中,BD、AE分别是△ABC的角平分线和高线,过点D作DF⊥AB于点F,若AB=4,BC=6,DF=2,则AE的长为( )
A.3 B. C. D.
6.如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC,∠DAM=35°,则∠MAB等于( )
A.35° B.55° C.70° D.20°
7.如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=5,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.5
8.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
二、填空题(满分32分)
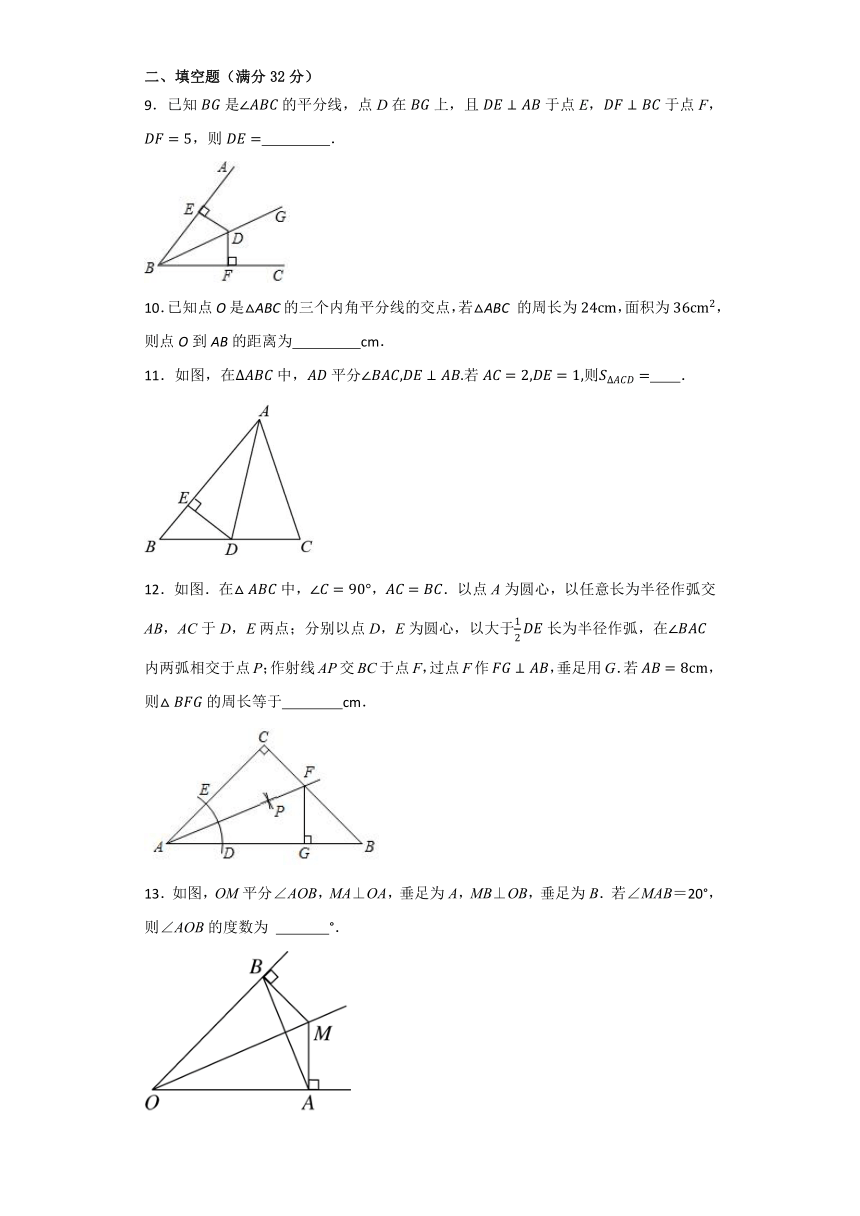
9.已知是的平分线,点D在上,且于点E,于点F,,则 .
10.已知点O是△ABC的三个内角平分线的交点,若△ABC 的周长为,面积为,则点O到AB的距离为 cm.
11.如图,在中,平分若则 .
12.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于 cm.
13.如图,OM平分∠AOB,MA⊥OA,垂足为A,MB⊥OB,垂足为B.若∠MAB=20°,则∠AOB的度数为 °.
14.如图,ABCD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是 .
15.如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P,PF⊥AB,垂足为F,PF=3,则点P到AC的距离为 .
16.如图,中,、的角平分线、交于点,延长、,,,则下列结论中正确的是 .(填序号)①平分;②;③;④.
三、解答题(满分56分)
17.作图:
如图,,按以下步骤使用尺规作图(保留作图痕迹,不写作法):
①作的平分线;
②在上任意画出点E(不与点A重合);
③连接.
问题:
(1)说明平分的理由;
(2)判断与的数量关系,并说明理由.(提示:为说明方便,可直接在尺规作图后的图中添加字母或线段)
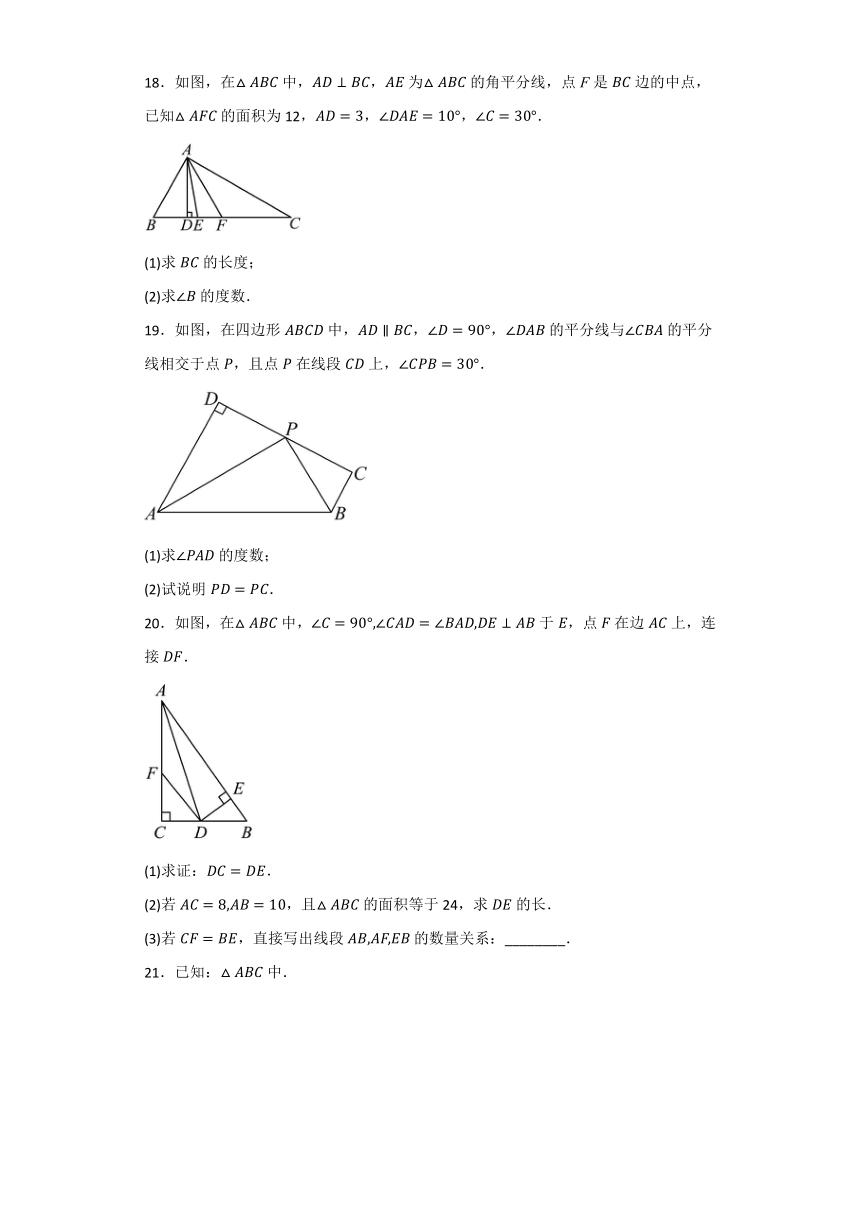
18.如图,在中,,为的角平分线,点F是边的中点,已知的面积为12,,,.
(1)求的长度;
(2)求的度数.
19.如图,在四边形中,,,的平分线与的平分线相交于点,且点在线段上,.
(1)求的度数;
(2)试说明.
20.如图,在中,于,点在边上,连接.
(1)求证:.
(2)若,且的面积等于24,求的长.
(3)若,直接写出线段的数量关系:________.
21.已知:中.
(1)如图,的角平分线、交于点.若,求的度数;
(2)如图,用无刻度的直尺和圆规在的边上找一点,使得.(不写作法,保留作图痕迹)
22.在中,,线段、分别平分、交于点G.
(1)如图1,求的度数;
(2)如图2,求证:;
(3)如图3,过点C作交延长线于点D,连接,点N在延长线上,连接交于点,使,若,,求线段的长.
参考答案
1.解:∵度假村在三条公路围成的平地上且到三条公路的距离相等,
∴度假村应该在△ABC三条角平分线的交点处.
故选:B.
2.解:∵OP平分∠BOA,PC⊥OA,PD⊥OB,
∴PC=PD,∠DOP=∠COP,且OP=OP,故A正确,
∴△ODP≌△OCP(HL),
∴OD=OC,∠CPO=∠DPO,故B,D正确,
故选C.
3.解:如图,过D作DE⊥AB交BA的延长线于E,
∵BD平分∠ABC,∠BCD=90°,
∴DE=CD=5,
∴四边形ABCD的面积.故选:A.
4.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得:DE=3,
∴CD=3.
故选:B.
5.解:如图所示,过作于,
平分,,,
,
,
,
即,
,
故选:C.
6.解:过点M作ME⊥AD于E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴ME=MC,
∵MC=MB,
∴ME=MB,
∵ME⊥AD,∠B=90°,
∴AM平分∠DAB,
∵∠DAM=35°,
∴∠MAB=∠DAM=35°,
故选:A.
7.解:当DP⊥AB时,根据垂线段最短可知,此时DP的值最小.
由作图可知:AE平分∠BAC,
∵∠C=90°,
∴DC⊥AC,
∵DP⊥AB,
∴DP=CD=5,
∴PD的最小值为5,
故选:D.
8.解:连接AD,过D点作DE⊥AB于点E,作DF⊥AC于点F,作DG⊥BC于点G,
∵△ABC的两条内角平分线相交于点D,
∴DE=DF=DG,
设MN平分△ABC的面积,则+=++,
∵=BM DE,=AM DE,=AC DF,=NC DG,=BN DG,
∴BM DE+BN DG=AM DE+AC DF+NC DG,
∴BM+BN=AM+AC+NC,
∴BM+BN+MN=AM+AC+NC+MN,
即这条直线分成的两个图形的周长比是1:1;
故选:B
9.解:∵BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,
∴DE=DF=5.
故答案为:5.
10.解:连接OA、OB、OC,作OD⊥AB于D,OF⊥AC于F,OE⊥BC于E,
∵OB平分∠ABC,OD⊥AB,OE⊥BC,
∴OD=OE,
同理,OD=OE=OF,
∵△ABC 的周长为,面积为,
则AB OD+AC OF+CB OE=36,即×(AB+AC+BC)×OD=36,
∴OD=3(cm),
∴点O到AB的距离为3
故答案为:3.
11.解:如图,作于点F,
∵平分,,,
∴,
∴.
故答案为:1.
12.解:根据题意,
在中,,,
由角平分线的性质,得,
∴的周长为:
;
故答案为:8
13.解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,
∴,
∵,
∴,
∴,
∵四边形OAMB的内角和为,
∴,
故答案为:40
14.解:过点P作于E.
∵,,
∴.
∵BP和CP分别平分和,, ,,
∴.
∵,
∴,
即点P到BC的距离是5.
故答案为:5.
15.解:
如图,作PH⊥AC于点H,PG⊥BC于点G,
∵BD平分∠CBF,CE平分∠HCB
∴PG=PF,PG=PH
∴PH= PF
∵PF=3
∴PH=3
∴点P到AC的距离为3,
故答案为:3.
16.解:①过点作于,
∵平分,平分,,,,
,,
,
点在的角平分线上,故①正确;
②∵,,
,
.
在和中,,
,
,
同理:,
,
,
,②正确;
③∵平分,平分,
,,
,③正确;
④由②可知,
,,
,故④正确.
故答案为:①②③④.
17.解:(1)尺规作图如下(作法不唯一).
证明:根据作图痕迹可知,,,,
所以,所以,所以AD平分.
(2)解:.
理由如下:
因为,,,
所以(SAS),所以.
18.(1)解:∵点F是边的中点,
∴,,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
又∵,
∴,
∵为的角平分线,
∴,
∴;
19.解:(1)∵,
∴.
∵,
∴.
∵平分,
∴.
∵,
∴,
∴.
∵平分,
∴.
(2)如图.过点作于点.
∵平分,,,
∴.
∵平分,,,
∴,
∴.
20.(1)证明:,,
∴;
(2)解:,
,
又,,且的面积等于24,
,
;
(3)解:∵,
在和中,
,
,
,
,
,
,,
.
21.解:(1)∵平分,平分,
∴,,
∵,,
∴,
∴,
∴,
(2)如图,由(1)得:要使,
作平分线,
过作平分线的垂线,交于点,
∴点即为所求.
22.(1)解:在中,,
∵
∴,
∵平分、平分,
∴,,
∴,
在中,,
∴.
(2)解:作平分交于点,如图所示:
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:作交延长线于点,作交延长线于点,作于点,如图所示:
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴平分,
∵,,
∴,
∵平分,,,
∴,
∴,
∴平分,
∵,
∴,
∴,
由(1)得,
∴,
∵,
,
,
∴,
∵,
∴,
由(2)得,
∴,
∴,
,
∵,
,
∴,
∴,
∴,
∵,
∴,
作于点,于点,于点,
∵,
∴,
,
,
∴,
∴,
∴.
一、单选题(满分32分)
1.如图,为促进某地旅游业的发展,当地旅游部门要在三条公路AB,AC,BC两两相交后围成的三角形区域内修建一个度假村,若这个度假村到三条公路的距离相等,则度假村应建在( )
A.三边的垂直平分线的交点上 B.三条角平分线的交点上
C.三条高线的交点上 D.三边中线的交点上
2.如图,OP平分∠BOA,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论中错误的是( )
A.PC=PD B.OC=OD C.OC=OP D.∠CPO=∠DPO
3.如图,已知在四边形中,,平分,,,,则四边形的面积是( )
A.40 B.42 C.46 D.48
4.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.2 B.3 C.4 D.5
5.如图,在△ABC中,BD、AE分别是△ABC的角平分线和高线,过点D作DF⊥AB于点F,若AB=4,BC=6,DF=2,则AE的长为( )
A.3 B. C. D.
6.如图,已知∠B=∠C=90°,M是BC的中点,DM平分∠ADC,∠DAM=35°,则∠MAB等于( )
A.35° B.55° C.70° D.20°
7.如图,Rt△ABC中,∠C=90°,用尺规作图法作出射线AE,AE交BC于点D,CD=5,P为AB上一动点,则PD的最小值为( )
A.2 B.3 C.4 D.5
8.如图,△ABC的两条内角平分线相交于点D,过点D作一条平分△ABC面积的直线,那么这条直线分成的两个图形的周长比是( )
A.2:1 B.1:1 C.2:3 D.3:1
二、填空题(满分32分)
9.已知是的平分线,点D在上,且于点E,于点F,,则 .
10.已知点O是△ABC的三个内角平分线的交点,若△ABC 的周长为,面积为,则点O到AB的距离为 cm.
11.如图,在中,平分若则 .
12.如图.在中,,.以点A为圆心,以任意长为半径作弧交AB,AC于D,E两点;分别以点D,E为圆心,以大于长为半径作弧,在内两弧相交于点P;作射线AP交BC于点F,过点F作,垂足用G.若,则的周长等于 cm.
13.如图,OM平分∠AOB,MA⊥OA,垂足为A,MB⊥OB,垂足为B.若∠MAB=20°,则∠AOB的度数为 °.
14.如图,ABCD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=10,则点P到BC的距离是 .
15.如图,△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P,PF⊥AB,垂足为F,PF=3,则点P到AC的距离为 .
16.如图,中,、的角平分线、交于点,延长、,,,则下列结论中正确的是 .(填序号)①平分;②;③;④.
三、解答题(满分56分)
17.作图:
如图,,按以下步骤使用尺规作图(保留作图痕迹,不写作法):
①作的平分线;
②在上任意画出点E(不与点A重合);
③连接.
问题:
(1)说明平分的理由;
(2)判断与的数量关系,并说明理由.(提示:为说明方便,可直接在尺规作图后的图中添加字母或线段)
18.如图,在中,,为的角平分线,点F是边的中点,已知的面积为12,,,.
(1)求的长度;
(2)求的度数.
19.如图,在四边形中,,,的平分线与的平分线相交于点,且点在线段上,.
(1)求的度数;
(2)试说明.
20.如图,在中,于,点在边上,连接.
(1)求证:.
(2)若,且的面积等于24,求的长.
(3)若,直接写出线段的数量关系:________.
21.已知:中.
(1)如图,的角平分线、交于点.若,求的度数;
(2)如图,用无刻度的直尺和圆规在的边上找一点,使得.(不写作法,保留作图痕迹)
22.在中,,线段、分别平分、交于点G.
(1)如图1,求的度数;
(2)如图2,求证:;
(3)如图3,过点C作交延长线于点D,连接,点N在延长线上,连接交于点,使,若,,求线段的长.
参考答案
1.解:∵度假村在三条公路围成的平地上且到三条公路的距离相等,
∴度假村应该在△ABC三条角平分线的交点处.
故选:B.
2.解:∵OP平分∠BOA,PC⊥OA,PD⊥OB,
∴PC=PD,∠DOP=∠COP,且OP=OP,故A正确,
∴△ODP≌△OCP(HL),
∴OD=OC,∠CPO=∠DPO,故B,D正确,
故选C.
3.解:如图,过D作DE⊥AB交BA的延长线于E,
∵BD平分∠ABC,∠BCD=90°,
∴DE=CD=5,
∴四边形ABCD的面积.故选:A.
4.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得:DE=3,
∴CD=3.
故选:B.
5.解:如图所示,过作于,
平分,,,
,
,
,
即,
,
故选:C.
6.解:过点M作ME⊥AD于E,
∵DM平分∠ADC,∠C=90°,ME⊥AD,
∴ME=MC,
∵MC=MB,
∴ME=MB,
∵ME⊥AD,∠B=90°,
∴AM平分∠DAB,
∵∠DAM=35°,
∴∠MAB=∠DAM=35°,
故选:A.
7.解:当DP⊥AB时,根据垂线段最短可知,此时DP的值最小.
由作图可知:AE平分∠BAC,
∵∠C=90°,
∴DC⊥AC,
∵DP⊥AB,
∴DP=CD=5,
∴PD的最小值为5,
故选:D.
8.解:连接AD,过D点作DE⊥AB于点E,作DF⊥AC于点F,作DG⊥BC于点G,
∵△ABC的两条内角平分线相交于点D,
∴DE=DF=DG,
设MN平分△ABC的面积,则+=++,
∵=BM DE,=AM DE,=AC DF,=NC DG,=BN DG,
∴BM DE+BN DG=AM DE+AC DF+NC DG,
∴BM+BN=AM+AC+NC,
∴BM+BN+MN=AM+AC+NC+MN,
即这条直线分成的两个图形的周长比是1:1;
故选:B
9.解:∵BG是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F,
∴DE=DF=5.
故答案为:5.
10.解:连接OA、OB、OC,作OD⊥AB于D,OF⊥AC于F,OE⊥BC于E,
∵OB平分∠ABC,OD⊥AB,OE⊥BC,
∴OD=OE,
同理,OD=OE=OF,
∵△ABC 的周长为,面积为,
则AB OD+AC OF+CB OE=36,即×(AB+AC+BC)×OD=36,
∴OD=3(cm),
∴点O到AB的距离为3
故答案为:3.
11.解:如图,作于点F,
∵平分,,,
∴,
∴.
故答案为:1.
12.解:根据题意,
在中,,,
由角平分线的性质,得,
∴的周长为:
;
故答案为:8
13.解:∵OM平分∠AOB,MA⊥OA,MB⊥OB,
∴,
∵,
∴,
∴,
∵四边形OAMB的内角和为,
∴,
故答案为:40
14.解:过点P作于E.
∵,,
∴.
∵BP和CP分别平分和,, ,,
∴.
∵,
∴,
即点P到BC的距离是5.
故答案为:5.
15.解:
如图,作PH⊥AC于点H,PG⊥BC于点G,
∵BD平分∠CBF,CE平分∠HCB
∴PG=PF,PG=PH
∴PH= PF
∵PF=3
∴PH=3
∴点P到AC的距离为3,
故答案为:3.
16.解:①过点作于,
∵平分,平分,,,,
,,
,
点在的角平分线上,故①正确;
②∵,,
,
.
在和中,,
,
,
同理:,
,
,
,②正确;
③∵平分,平分,
,,
,③正确;
④由②可知,
,,
,故④正确.
故答案为:①②③④.
17.解:(1)尺规作图如下(作法不唯一).
证明:根据作图痕迹可知,,,,
所以,所以,所以AD平分.
(2)解:.
理由如下:
因为,,,
所以(SAS),所以.
18.(1)解:∵点F是边的中点,
∴,,
∴,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
∵,
∴,
又∵,
∴,
∵为的角平分线,
∴,
∴;
19.解:(1)∵,
∴.
∵,
∴.
∵平分,
∴.
∵,
∴,
∴.
∵平分,
∴.
(2)如图.过点作于点.
∵平分,,,
∴.
∵平分,,,
∴,
∴.
20.(1)证明:,,
∴;
(2)解:,
,
又,,且的面积等于24,
,
;
(3)解:∵,
在和中,
,
,
,
,
,
,,
.
21.解:(1)∵平分,平分,
∴,,
∵,,
∴,
∴,
∴,
(2)如图,由(1)得:要使,
作平分线,
过作平分线的垂线,交于点,
∴点即为所求.
22.(1)解:在中,,
∵
∴,
∵平分、平分,
∴,,
∴,
在中,,
∴.
(2)解:作平分交于点,如图所示:
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴;
(3)解:作交延长线于点,作交延长线于点,作于点,如图所示:
∵平分,
∴,
∵,
∴,
∴,
∵,
∴,
∴平分,
∵,,
∴,
∵平分,,,
∴,
∴,
∴平分,
∵,
∴,
∴,
由(1)得,
∴,
∵,
,
,
∴,
∵,
∴,
由(2)得,
∴,
∴,
,
∵,
,
∴,
∴,
∴,
∵,
∴,
作于点,于点,于点,
∵,
∴,
,
,
∴,
∴,
∴.
