12.2三角形全等的判定 同步测试题(含解析)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 12.2三角形全等的判定 同步测试题(含解析)2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 00:00:00 | ||
图片预览



文档简介
2023-2024学年人教版八年级数学上册《12.2三角形全等的判定》
同步测试题(附答案)
一、单选题(满分28分)
1.已知:如图,点A、D、B、E在同一直线上,且,,增加下列条件不能推导出的是( )
A. B. C. D.
2.给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )
A., B.,
C., D.,
3.如图,在四边形ABCD中,F是对角线AC的中点,连接DF并延长交BC于点E,若,,,则四边形的面积为( )
A.1 B.2 C.3 D.4
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
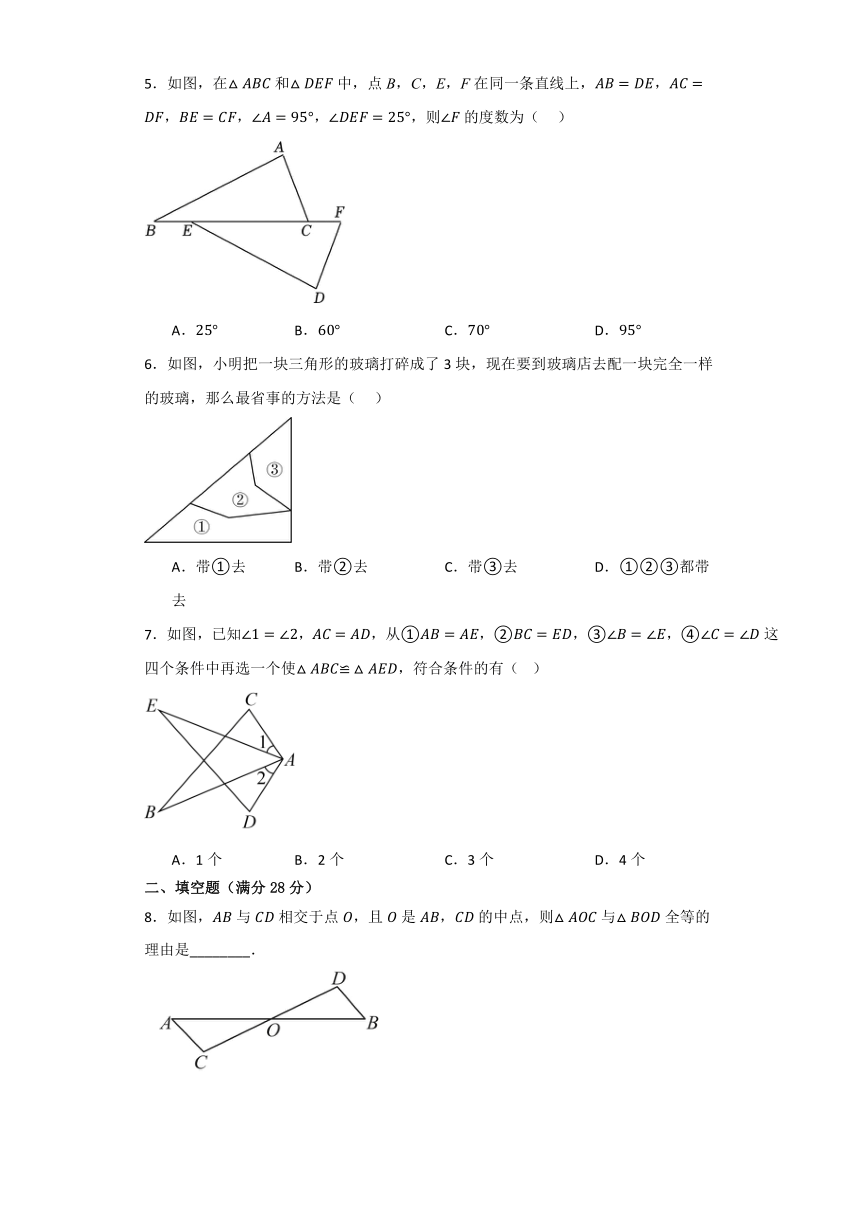
5.如图,在和中,点B,C,E,F在同一条直线上,,则的度数为( )
A. B. C. D.
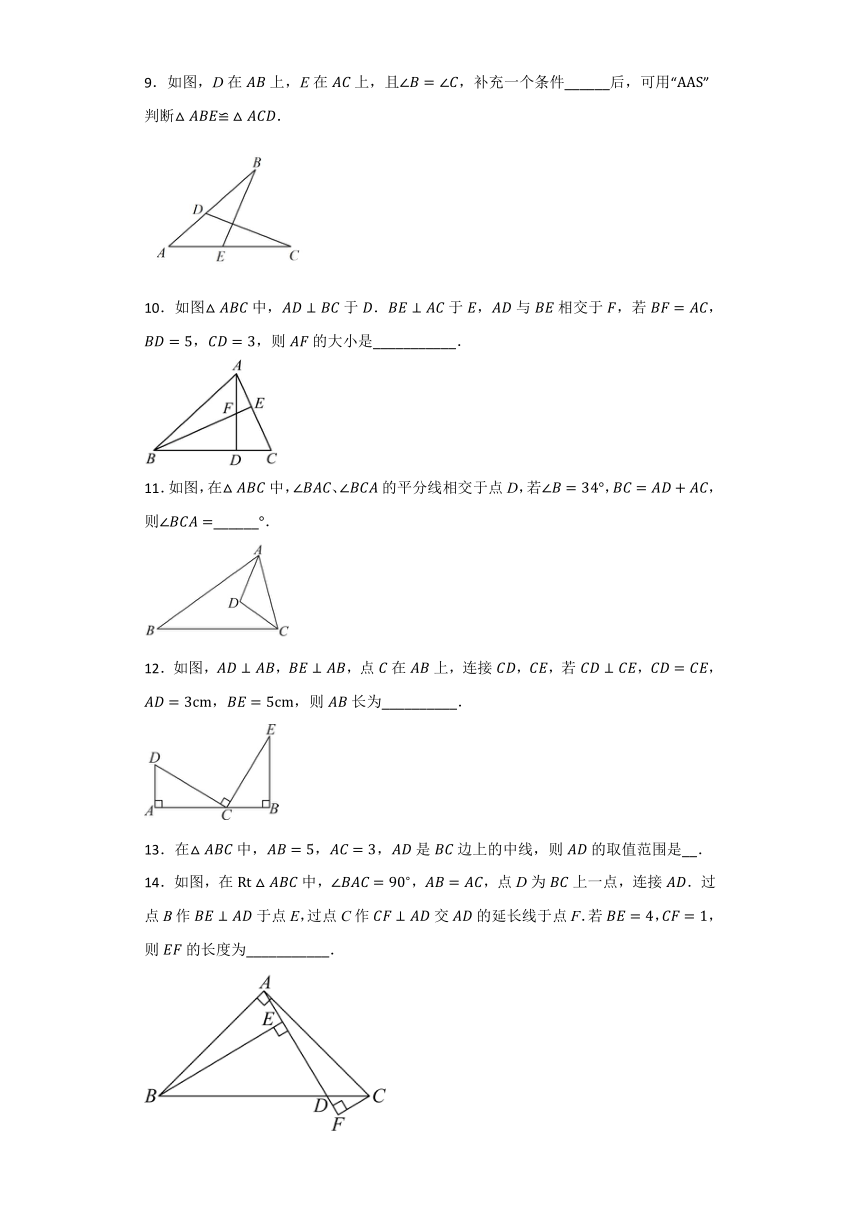
6.如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
7.如图,已知,,从①,②,③,④这四个条件中再选一个使,符合条件的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(满分28分)
8.如图,与相交于点,且是的中点,则与全等的理由是________.
9.如图,D在上,E在上,且,补充一个条件______后,可用“”判断.
10.如图中,于.于,与相交于,若,,,则的大小是___________.
11.如图,在中,、的平分线相交于点D,若,,则______.
12.如图,,,点在上,连接,,若,,,,则长为__________.
13.在中,,是边上的中线,则的取值范围是__.
14.如图,在中,,,点D为上一点,连接.过点B作于点E,过点C作交的延长线于点F.若,,则的长度为___________.
三、解答题(满分44分)
15.如图在中,D是边上的一点,,平分,交边于点E,连接.
(1)求证:;
(2)若,求的度数.
16.如图,中,点D是延长线上一点,满足,过点D作,连接,使.
(1)求证:.
(2)如果,,求的长.
17.将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
18.问题:如图,在中,,,平分,于点E,说明的理由.
分析:要说明“一条线段等于另一条线段的两倍”,我们容易想到“线段的中点”和“等腰三角形的三线合一”两个基本图形.
如图1,若点C是线段AB的中点,则.
如图2,在中,若,于点D,则.
要求:请根据上述分析完成上述问题的解答.
19.如图,是经过顶点C的一条直线,,E、F分别是直线上两点,且.
(1)若直线经过的内部,且E、F在射线上.
①如图1,若,,试判断和的数量关系,并说明理由.
②如图2,若,请添加一个关于与关系的条件______,使①中的结论仍然成立;
(2)如图3,若直线经过的外部,,请提出关于,,三条线段数量关系的合理猜想,并说明理由.
20.(1)如图1,中,,,,、分别是、上的点,且.探究图中线段,,之间的数量关系是______.
(2)如图2,若在四边形中,,,E,F分别是、上的点,且,上述结论是否仍然成立,并说明理由.
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以80海里/小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角,试求此时两舰艇之间的距离.
参考答案
1.解:∵,
∴,
即,
∵,
∴,
当时,为,不能判定;
当时,,满足,可以判定;
当时,满足,可以判定
当时,,满足,可以判定,
故选A.
2.解:A.,,增加“”后,类似,不能判定两三角形全等,所以所画出的三角形的形状和大小仍不能完全确定,故选项A符合题意.
B.,,增加“”后,属于用来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项B不符合题意.
C.,,增加“”后,属于用来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项C不符合题意.
D.,,增加“”后,属于用SSS 来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项D不符合题意.
故选:A.
3.解:∵F是对角线AC的中点,
∴
在和中,
∴(SAS),
∴,,
∴,,
如图,过点D作于点H,
∴,,
∴,
∴.
故选:D
4.解∶在和中
,
∴,
∴,
又米,
∴米.
故选∶B.
5.解:∵,
∴,即,
又∵,
∴,
∴,
∴,
故选B.
6.解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃.
故选:A.
7.解:∵,
∴,
即,
①∵,,
∴,故①正确;
添加③,则
添加④,则
添加条件②,不能证明,
故选:C.
8.解:∵是的中点,
∴
在和中,
∴,
故答案为:.
9.解:∵,,
∴若用“”判断,可补充的条件是或;
故答案为:或.
10.解:于,于
,,
又(对顶角相等)
,
在和中,
,
,
,,
,
故答案为:2.
11.解:在上取,连接,,
平分,
,
又,
,
,,
,
,
,
、的平分线相交于点,
平分,
.
,
,
,
,
,
,
故答案为:78.
12.解:,
,
,
,
,
,
在和中,
,
,
,,
.
故答案为:.
13.解:如图,延长到E,使,
∵是边上的中线,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
即,
∴.
故答案为:.
14.解: ∵,
∴,
∵,,
∴,
∴,
∴,
在和中:
,
∴,
∴,
∴,
故答案为:3.
15.(1)解:∵平分,
∴.
∵,
∴;
(2)解:∵,
∴,
∴.
16.(1)解:∵,
∴,
在与中,
∴
(2)∵,
∴
又∵,,
∴
17.(1)解:因为,
所以,
即.
在和中,
,
所以.
(2)因为,
所以,.
在和中,
,
所以,
所以,
所以.
18.解:延长,,交于点F,
∵,
∴,,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵,
∴.
19.(1)解:①,理由如下:
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
②添加,使①中的结论仍然成立,理由如下:
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴;
故答案为:;
(2),理由如下:
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,,
∴,
即.
20.解:(1)如图1,,
理由如下:在和中,
,
,
,,
,
,
,
在和中,
,
,
,
,
;
(2)如图2,(1)中的结论仍然成立,即.
理由:延长到点.使.连接,
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
,
;
(3)如图3,连接,延长、相交于点,
,,
,
,,
符合(2)中的条件,
结论成立,
即(海里).
此时两舰艇之间的距离为210海里.
同步测试题(附答案)
一、单选题(满分28分)
1.已知:如图,点A、D、B、E在同一直线上,且,,增加下列条件不能推导出的是( )
A. B. C. D.
2.给定三角形的两个元素,画出的三角形的形状和大小都是不能确定的,在下列给定的条件下,再增加一个“”的条件后,所画出的三角形形状和大小仍不能完全确定的是( )
A., B.,
C., D.,
3.如图,在四边形ABCD中,F是对角线AC的中点,连接DF并延长交BC于点E,若,,,则四边形的面积为( )
A.1 B.2 C.3 D.4
4.如图,为测量池塘两端A、B的距离,小康在池塘外一块平地上选取了一点O,连接,,并分别延长,到点C,D,使得,,连接,测得的长为165米,则池塘两端A,B之间的距离为( )
A.160米 B.165米 C.170米 D.175米
5.如图,在和中,点B,C,E,F在同一条直线上,,则的度数为( )
A. B. C. D.
6.如图,小明把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
7.如图,已知,,从①,②,③,④这四个条件中再选一个使,符合条件的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(满分28分)
8.如图,与相交于点,且是的中点,则与全等的理由是________.
9.如图,D在上,E在上,且,补充一个条件______后,可用“”判断.
10.如图中,于.于,与相交于,若,,,则的大小是___________.
11.如图,在中,、的平分线相交于点D,若,,则______.
12.如图,,,点在上,连接,,若,,,,则长为__________.
13.在中,,是边上的中线,则的取值范围是__.
14.如图,在中,,,点D为上一点,连接.过点B作于点E,过点C作交的延长线于点F.若,,则的长度为___________.
三、解答题(满分44分)
15.如图在中,D是边上的一点,,平分,交边于点E,连接.
(1)求证:;
(2)若,求的度数.
16.如图,中,点D是延长线上一点,满足,过点D作,连接,使.
(1)求证:.
(2)如果,,求的长.
17.将两个三角形纸板和按如图所示的方式摆放,连接.已知,,.
(1)试说明.
(2)若,求的度数.
18.问题:如图,在中,,,平分,于点E,说明的理由.
分析:要说明“一条线段等于另一条线段的两倍”,我们容易想到“线段的中点”和“等腰三角形的三线合一”两个基本图形.
如图1,若点C是线段AB的中点,则.
如图2,在中,若,于点D,则.
要求:请根据上述分析完成上述问题的解答.
19.如图,是经过顶点C的一条直线,,E、F分别是直线上两点,且.
(1)若直线经过的内部,且E、F在射线上.
①如图1,若,,试判断和的数量关系,并说明理由.
②如图2,若,请添加一个关于与关系的条件______,使①中的结论仍然成立;
(2)如图3,若直线经过的外部,,请提出关于,,三条线段数量关系的合理猜想,并说明理由.
20.(1)如图1,中,,,,、分别是、上的点,且.探究图中线段,,之间的数量关系是______.
(2)如图2,若在四边形中,,,E,F分别是、上的点,且,上述结论是否仍然成立,并说明理由.
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东的方向以80海里/小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角,试求此时两舰艇之间的距离.
参考答案
1.解:∵,
∴,
即,
∵,
∴,
当时,为,不能判定;
当时,,满足,可以判定;
当时,满足,可以判定
当时,,满足,可以判定,
故选A.
2.解:A.,,增加“”后,类似,不能判定两三角形全等,所以所画出的三角形的形状和大小仍不能完全确定,故选项A符合题意.
B.,,增加“”后,属于用来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项B不符合题意.
C.,,增加“”后,属于用来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项C不符合题意.
D.,,增加“”后,属于用SSS 来判定三角形全等,所以所画出的三角形的形状和大小确定,故选项D不符合题意.
故选:A.
3.解:∵F是对角线AC的中点,
∴
在和中,
∴(SAS),
∴,,
∴,,
如图,过点D作于点H,
∴,,
∴,
∴.
故选:D
4.解∶在和中
,
∴,
∴,
又米,
∴米.
故选∶B.
5.解:∵,
∴,即,
又∵,
∴,
∴,
∴,
故选B.
6.解:第①块不仅保留了原来三角形的两个角还保留了一边,则可以根据来配一块一样的玻璃.
故选:A.
7.解:∵,
∴,
即,
①∵,,
∴,故①正确;
添加③,则
添加④,则
添加条件②,不能证明,
故选:C.
8.解:∵是的中点,
∴
在和中,
∴,
故答案为:.
9.解:∵,,
∴若用“”判断,可补充的条件是或;
故答案为:或.
10.解:于,于
,,
又(对顶角相等)
,
在和中,
,
,
,,
,
故答案为:2.
11.解:在上取,连接,,
平分,
,
又,
,
,,
,
,
,
、的平分线相交于点,
平分,
.
,
,
,
,
,
,
故答案为:78.
12.解:,
,
,
,
,
,
在和中,
,
,
,,
.
故答案为:.
13.解:如图,延长到E,使,
∵是边上的中线,,
∴,
在和中,
,
∴,
∴,
∵,
∴,
即,
∴.
故答案为:.
14.解: ∵,
∴,
∵,,
∴,
∴,
∴,
在和中:
,
∴,
∴,
∴,
故答案为:3.
15.(1)解:∵平分,
∴.
∵,
∴;
(2)解:∵,
∴,
∴.
16.(1)解:∵,
∴,
在与中,
∴
(2)∵,
∴
又∵,,
∴
17.(1)解:因为,
所以,
即.
在和中,
,
所以.
(2)因为,
所以,.
在和中,
,
所以,
所以,
所以.
18.解:延长,,交于点F,
∵,
∴,,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∵平分,
∴,
在和中,
,
∴,
∴,
∵,
∴.
19.(1)解:①,理由如下:
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴;
②添加,使①中的结论仍然成立,理由如下:
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴;
故答案为:;
(2),理由如下:
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,,
∴,
即.
20.解:(1)如图1,,
理由如下:在和中,
,
,
,,
,
,
,
在和中,
,
,
,
,
;
(2)如图2,(1)中的结论仍然成立,即.
理由:延长到点.使.连接,
在和中,
,
,
,,
,
,
,
在和中,
,
,
,
,
;
(3)如图3,连接,延长、相交于点,
,,
,
,,
符合(2)中的条件,
结论成立,
即(海里).
此时两舰艇之间的距离为210海里.
