勾股定理第一课时(浙江省台州市)
文档属性
| 名称 | 勾股定理第一课时(浙江省台州市) |  | |
| 格式 | rar | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-02 00:43:00 | ||
图片预览



文档简介
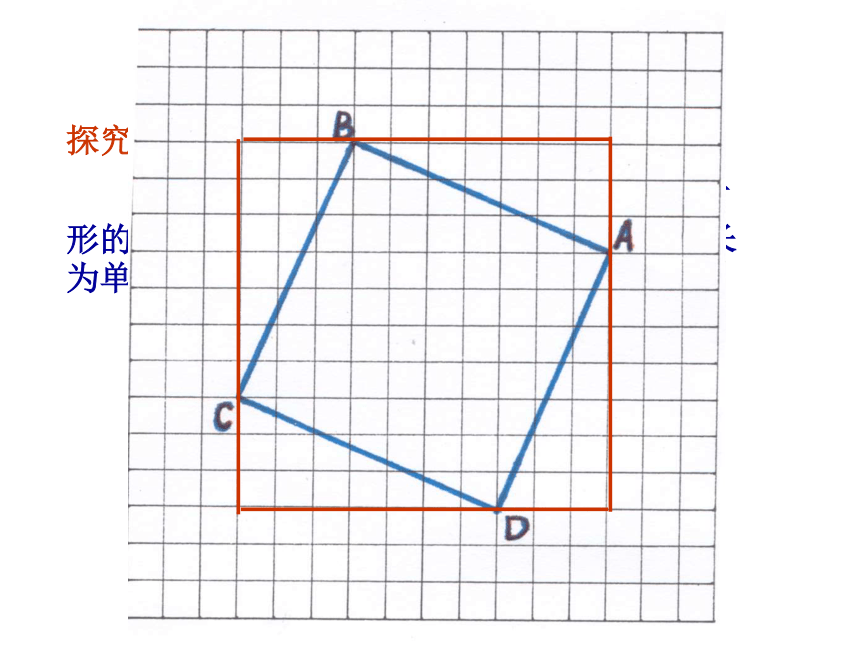
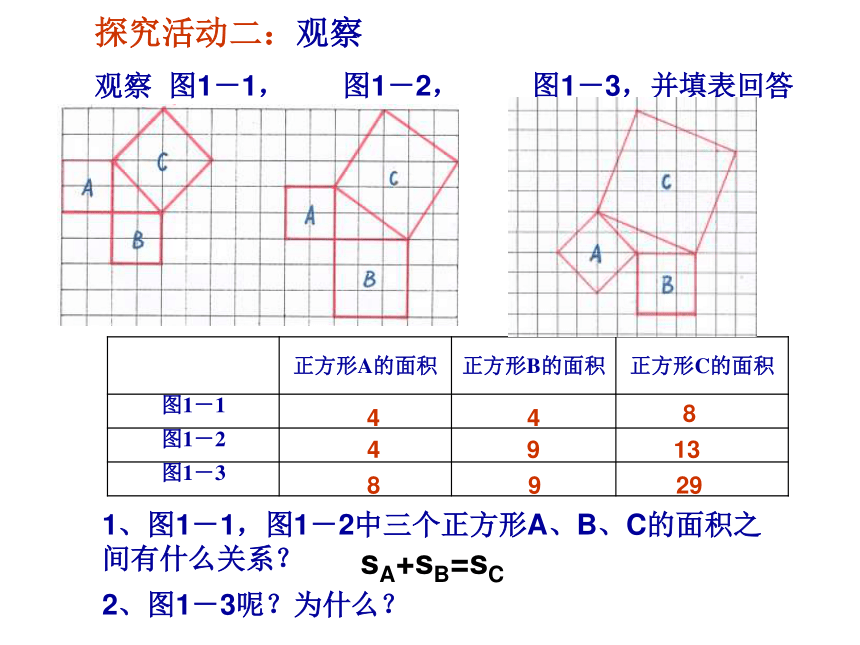
课件28张PPT。勾股定理执教:敬业中学 徐颖锦探究活动二:观察观察 图1-1, 图1-2, 图1-3,并填表回答 sA+sB=sC
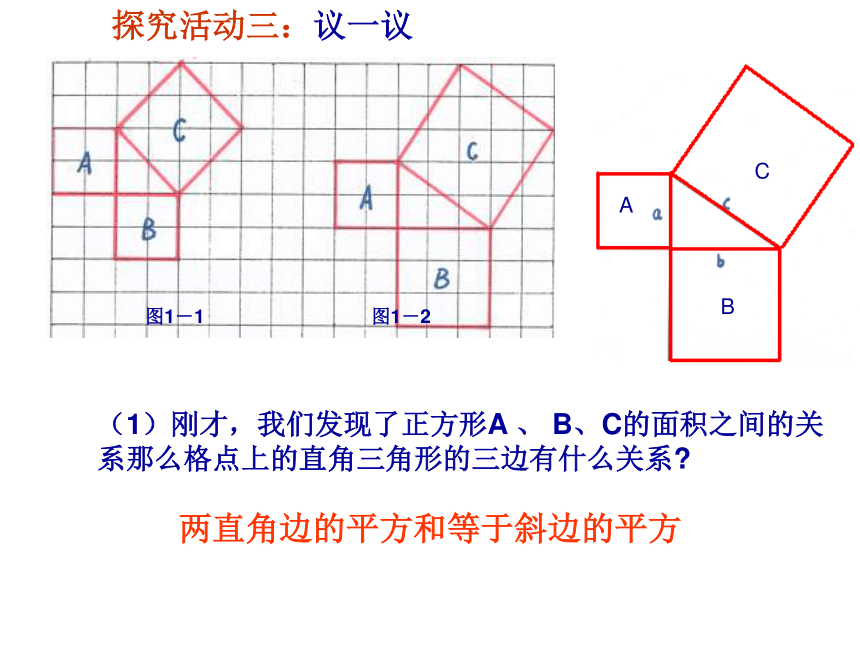
探究活动三:议一议(1)刚才,我们发现了正方形A 、 B、C的面积之间的关系那么格点上的直角三角形的三边有什么关系?
图1-1 图1-2 图1-4 ABC两直角边的平方和等于斜边的平方如果直角三角形的两直角边长分别
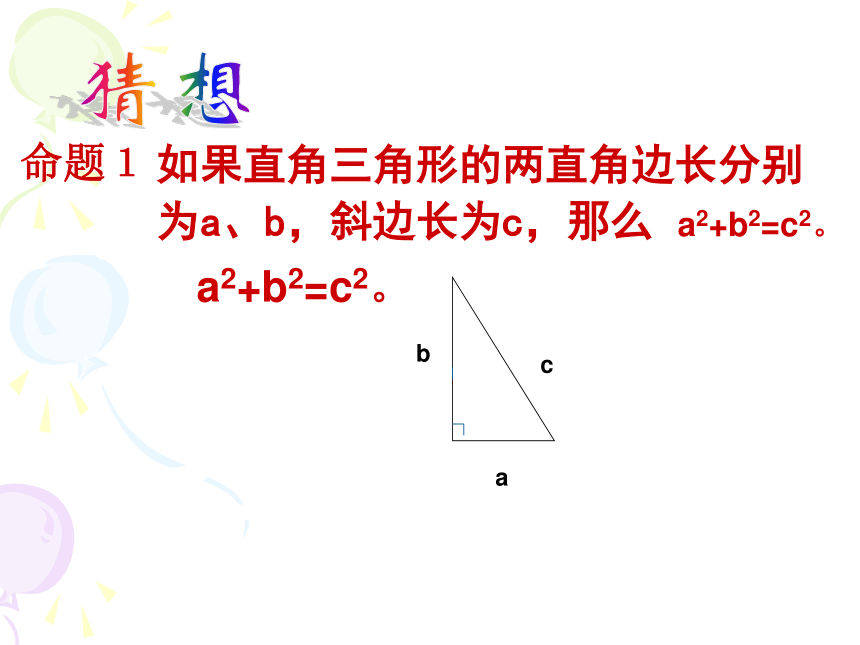
为a、b,斜边长为c,那么 a2+b2=c2。 abc a2+b2=c2。猜想命题1探究活动四:动手拼一拼abcb-a 同学们:拿出你手中准备好
的四个直角三角形,拼一拼,
动手动脑,试一试,你能用这一
只转动着的风车来验证猜想吗?
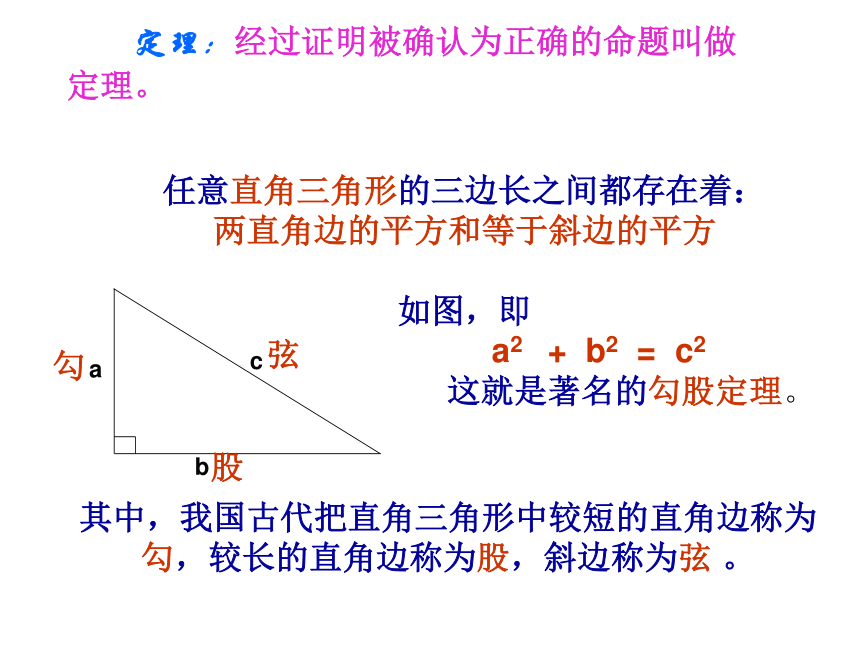
定理:经过证明被确认为正确的命题叫做
定理。 任意直角三角形的三边长之间都存在着:
两直角边的平方和等于斜边的平方
如图,即
a2 + b2 = c2
这就是著名的勾股定理。勾股弦其中,我国古代把直角三角形中较短的直角边称为
勾,较长的直角边称为股,斜边称为弦 。这个标志的设计基础是1700多年前,中国古代数学家赵爽的“弦图”,是为了证明发明于中国周代的勾股定理而绘制的。它既标志着中国古代数学的成就,又像一只转动着的风车欢迎来自世界各地的数学家们。 同学们:拿出你手中准备好的四个
直角三角形,拼一拼,动手动脑,
试一试,你能用这一只转动着
的风车来验证猜想吗?
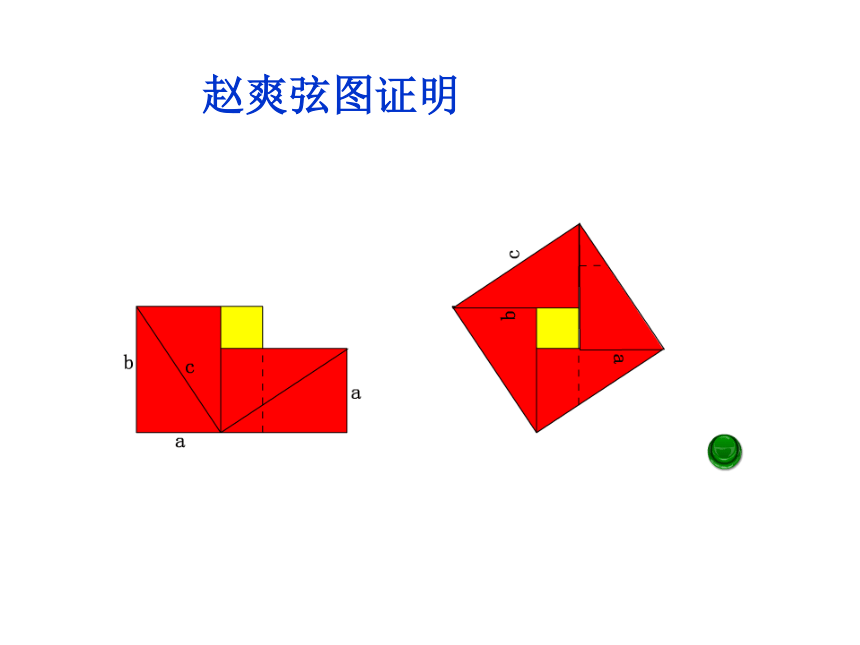
赵爽弦图证明在西方,勾股定理又称毕达哥拉斯定理.毕达哥拉斯是生活在2500年前的古希腊数学家、哲学家。他的一个学生希帕索斯通过勾股定理发现了无理数,从而导致第一次数学危机。毕达哥拉斯与勾股定理 伽菲尔德证法:aabbcc s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2应用一: 根据我国古算书《周髀算经》记载,在约公元
前1100年,人们就有“勾三、股四、弦五”的说法,
这一说法的依据是什么?勾股定理 32+42=52(1)解 ∵x2=62+82=100∴x=1 0(2)解:∵x2=132-122=25∴x=52、已知一直角三角形的两条边长为3,4,
求另一条边长?(1)两直角边长为3,4AB那么斜边长为5(2) AC=4,AB=3那么BC2=42-32=7那么BC= √7C解:此题分为两种情况:答:另一条边长为5或√7
应用三:小明妈妈买了一部29英寸(约74厘米)的电视机。小明量了电视机屏幕后,发现屏幕只有约58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗? 想一想:如下图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为
7cm。求A、B、C、D的面积之和。EEEEF试一试 如图,一根旗杆在离地5米处断裂,旗杆顶部落在离旗杆底部12米处.旗杆折断之前有多高?5米12米 1、本节课我们学到了什么? 2、你还有什么困惑? 小结:作业:1、通过查阅资料,了解勾股定理的文化背景。
2、收集有关勾股定理的证明方法,与同伴交流,
写一篇关于勾股定理证明的小论文。
再见
探究活动三:议一议(1)刚才,我们发现了正方形A 、 B、C的面积之间的关系那么格点上的直角三角形的三边有什么关系?
图1-1 图1-2 图1-4 ABC两直角边的平方和等于斜边的平方如果直角三角形的两直角边长分别
为a、b,斜边长为c,那么 a2+b2=c2。 abc a2+b2=c2。猜想命题1探究活动四:动手拼一拼abcb-a 同学们:拿出你手中准备好
的四个直角三角形,拼一拼,
动手动脑,试一试,你能用这一
只转动着的风车来验证猜想吗?
定理:经过证明被确认为正确的命题叫做
定理。 任意直角三角形的三边长之间都存在着:
两直角边的平方和等于斜边的平方
如图,即
a2 + b2 = c2
这就是著名的勾股定理。勾股弦其中,我国古代把直角三角形中较短的直角边称为
勾,较长的直角边称为股,斜边称为弦 。这个标志的设计基础是1700多年前,中国古代数学家赵爽的“弦图”,是为了证明发明于中国周代的勾股定理而绘制的。它既标志着中国古代数学的成就,又像一只转动着的风车欢迎来自世界各地的数学家们。 同学们:拿出你手中准备好的四个
直角三角形,拼一拼,动手动脑,
试一试,你能用这一只转动着
的风车来验证猜想吗?
赵爽弦图证明在西方,勾股定理又称毕达哥拉斯定理.毕达哥拉斯是生活在2500年前的古希腊数学家、哲学家。他的一个学生希帕索斯通过勾股定理发现了无理数,从而导致第一次数学危机。毕达哥拉斯与勾股定理 伽菲尔德证法:aabbcc s梯形= (a+b)(a+b)= (a2+2ab+b2)
= a2+ab+ b2
s梯形=2× ab+ c2=ab+ c2
∵s梯形=s梯形 ∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2应用一: 根据我国古算书《周髀算经》记载,在约公元
前1100年,人们就有“勾三、股四、弦五”的说法,
这一说法的依据是什么?勾股定理 32+42=52(1)解 ∵x2=62+82=100∴x=1 0(2)解:∵x2=132-122=25∴x=52、已知一直角三角形的两条边长为3,4,
求另一条边长?(1)两直角边长为3,4AB那么斜边长为5(2) AC=4,AB=3那么BC2=42-32=7那么BC= √7C解:此题分为两种情况:答:另一条边长为5或√7
应用三:小明妈妈买了一部29英寸(约74厘米)的电视机。小明量了电视机屏幕后,发现屏幕只有约58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗? 想一想:如下图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为
7cm。求A、B、C、D的面积之和。EEEEF试一试 如图,一根旗杆在离地5米处断裂,旗杆顶部落在离旗杆底部12米处.旗杆折断之前有多高?5米12米 1、本节课我们学到了什么? 2、你还有什么困惑? 小结:作业:1、通过查阅资料,了解勾股定理的文化背景。
2、收集有关勾股定理的证明方法,与同伴交流,
写一篇关于勾股定理证明的小论文。
再见
