数学人教A版(2019)必修第一册2.1等式性质与不等式性质课件(共36张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册2.1等式性质与不等式性质课件(共36张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 19:05:23 | ||
图片预览











文档简介
(共36张PPT)
第2章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【素养目标】
1.了解现实世界和日常生活中的等量关系与不等关系.(数学抽象)
2.了解不等式(组)的实际背景,会用不等式(组)表示不等关系.(数学建模)
3.掌握不等式的性质及应用.(逻辑推理)
4.会用作差法(或作商法)比较两个实数或代数式值的大小.(数学运算)
5.能运用等式的性质或不等式的性质解决相关问题.(逻辑推理)
【学法解读】
在相等关系与不等关系的学习中,学生通过类比学过的等式与不等式的性质,进一步探索等式与不等式的共性与差异.
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过或不少于等.类似于这样的问题,反映在数量关系上,就是相等与不等.相等用等式表示,不等用不等式表示.
【等式】指的是用等号“=”连接起来的式子.
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”连接起来的式子
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋白质的含量应不少于2.3%;
设该路段行驶的汽车速度为,则
,
问题1:不等关系及其表示
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ.
A
B
C
P
Q
你能写出其他的可能情况 吗?
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
设三角形三边分别为,则
【问题2】某种杂志原本以每本2.5元的价格出售,可以售出8万本.据市场调查发现,杂志的单价每提高0.1元,销售量就可能减少2000本.如何定价才能使涨价后的总收入不低于20万元
【分析】设涨价之后的杂志每本定价元,则销售总收入为
万元,
≥20,求出不等式的解,即可求出定价
所以用不等式表示为:
问题1:不等关系及其表示
问题2:不等式的性质
实际上,在初中我们已经通过具体实例归纳了一些不等式的性质.那么,这些性质为什么是正确的?还有其他不等式的性质吗?回答这些问题要用到关于两个实数大小关系的基本事实.
由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系:如图,设a,b是两个实数,它们在数轴上所对应的点分别是A,B,当点A在点B的左边时,ab.
如何解不等式 ≥20呢?
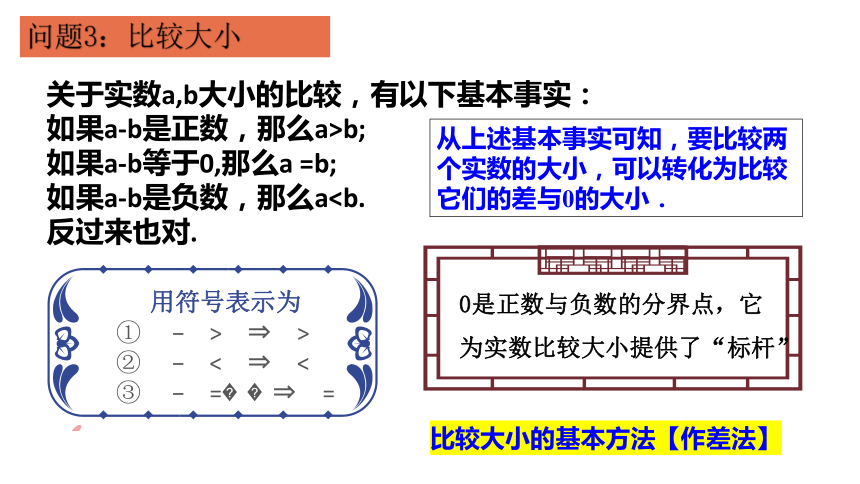
问题3:比较大小
关于实数a,b大小的比较,有以下基本事实:
如果a-b是正数,那么a>b;
如果a-b等于0,那么a =b;
如果a-b是负数,那么a反过来也对.
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
比较大小的基本方法【作差法】
用符号表示为
① > >
② < < ③ = =
0是正数与负数的分界点,它为实数比较大小提供了“标杆”
比较和的大小.
【解】运用作差法:
2>0,
所以>
0是正数与负数的分界线,它为比较实数的大小提供了标杆.
如图是根据第24届国际数学家大会的会标设计的,会标灵感来源于中国古代数学家赵爽的弦图,图中有什么不等关系?
很显然赵爽弦图是我们在初中研究勾股定理时的模型,我们把它抽象成如图所示的图形.
设图中直角三角形的两个直角边长为,那么正方形的边长就是,这样,四个直角三角形的面积之和就是,正方形的面积为,很显然正方形的面积大于三角形面积和.即
当直角三角形变为等腰直角三角形时,内部的小正方形变成了一个点,此时,有,所以综合可知,
问题4:一个重要不等式
一般地,,这个不等式被称为重要不等式,
当且仅当时,等号成立.
事实上,利用完全平方公式也可以得到这个不等式:
因为,,当且仅当时,等号成立.
所以
因此,由两个实数大小关系的基本事实,我们得到:
,当且仅当时,等号成立.
问题4:一个重要不等式
★性质1【对称性】
★性质2【传递性】
★性质3【加减性】
★性质4【同乘性】
★性质5【同除性】
如果,那么
如果,,那么
如果,那么
如果,那么
如果,,那么
思考
请你先梳理等式的基本性质,再观察它们的共性.你能归纳一下发现等式基本性质的方法吗?
可以发现,性质1,2反映了相等关系自身的特性,性质3,4,5是从运算的角度提出的,反映了等式在运算中保持的不变性.
问题5:等式有什么性质
★性质1【对称性】
★性质2【传递性】
如果,那么.即
如果,,那么.
即,
我们来证明性质2:
类比等式的性质1,2,我们可以猜想不等式有如下性质:
问题6:不等式有什么性质
★性质3
【可加性】
★性质4
【可乘性】
★性质5
【同向可加性】
如果,那么
如果,,那么;
如果,,那么
不等式两边同时加上一个数,不变号
不等式两边同时乘上一个正数,不变号;
如果,,那么
不等式两边同时乘上一个负数,要变号 .
如果,,那么
如果,,那么
问题6:不等式有什么性质
类比等式的性质3~5,可以猜想不等式还有如下性质:
★性质6
【同向同正可乘性】
★性质7
【同正可乘方性】
如果, ,那么
如果,那么
等式
不等式
问题6:不等式有什么性质
我的等号左右能对应加减乘除(除数不为0),你行吗?
我只有同向可加性,同向可乘还必须保证是正数!
例2 已知,,求证
【分析】因为,所以要证,可先证明
【证明】因为,所以, .
所以 ,
因为,所以,即
>
<
<
<
习题2.1
(第42页)
2.某市环保局为增加城市的绿地面积,提出两个投资方案:方案A为一次性投资500万元;方案B为第一年投资100万元,以后每年投资10万元.列出不等式表示“经过n年之后,方案B的投入不少于方案A的投入” .
4.一个大于50且小于60的两位数,其个位数字比十位数字大2.试用不等式表示上述关系,并求这个两位数(用a和b分别表示这个两位数的十位数字和个位数字).
B
9.证明:圆的面积大于与它具有相同周长的正方形的面积.并据此说明,人们通常把自来水管的横截面制成圆形,而不是正方形的原因.
所以圆的面积更大
原因:自来水管的横截面是圆形的,可以最大面积地使水通过,减少阻力.
12.火车站有某公司代运的甲种货物1 530 ,乙种货物1 150 .现计划用A,B两种型号的货厢共50节运送这批货物.已知35甲种货物和15乙种货物可装满一节A型货厢,25甲种货物和35乙种货物可装满一节B型货厢,据此安排A,B两种货厢的节数,共有几种方案?若每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元,哪种方案的运费较少?
所以共有三种方案,方案一:安排A型货厢28节,B型货厢22节;方案二:安排A型货厢29节,B型货厢21节;方案三:安排A型货厢30节,B型货厢20节.
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
第2章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
【素养目标】
1.了解现实世界和日常生活中的等量关系与不等关系.(数学抽象)
2.了解不等式(组)的实际背景,会用不等式(组)表示不等关系.(数学建模)
3.掌握不等式的性质及应用.(逻辑推理)
4.会用作差法(或作商法)比较两个实数或代数式值的大小.(数学运算)
5.能运用等式的性质或不等式的性质解决相关问题.(逻辑推理)
【学法解读】
在相等关系与不等关系的学习中,学生通过类比学过的等式与不等式的性质,进一步探索等式与不等式的共性与差异.
在现实世界和日常生活中,大量存在着相等关系和不等关系,例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重、不超过或不少于等.类似于这样的问题,反映在数量关系上,就是相等与不等.相等用等式表示,不等用不等式表示.
【等式】指的是用等号“=”连接起来的式子.
【不等式】指的是用不等号“≠”“>”“<”“≥”“≤”连接起来的式子
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速;;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋白质的含量应不少于2.3%;
设该路段行驶的汽车速度为,则
,
问题1:不等关系及其表示
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ.
A
B
C
P
Q
你能写出其他的可能情况 吗?
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
设三角形三边分别为,则
【问题2】某种杂志原本以每本2.5元的价格出售,可以售出8万本.据市场调查发现,杂志的单价每提高0.1元,销售量就可能减少2000本.如何定价才能使涨价后的总收入不低于20万元
【分析】设涨价之后的杂志每本定价元,则销售总收入为
万元,
≥20,求出不等式的解,即可求出定价
所以用不等式表示为:
问题1:不等关系及其表示
问题2:不等式的性质
实际上,在初中我们已经通过具体实例归纳了一些不等式的性质.那么,这些性质为什么是正确的?还有其他不等式的性质吗?回答这些问题要用到关于两个实数大小关系的基本事实.
由于数轴上的点与实数一一对应,所以可以利用数轴上点的位置关系来规定实数的大小关系:如图,设a,b是两个实数,它们在数轴上所对应的点分别是A,B,当点A在点B的左边时,a
如何解不等式 ≥20呢?
问题3:比较大小
关于实数a,b大小的比较,有以下基本事实:
如果a-b是正数,那么a>b;
如果a-b等于0,那么a =b;
如果a-b是负数,那么a
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
比较大小的基本方法【作差法】
用符号表示为
① > >
② < < ③ = =
0是正数与负数的分界点,它为实数比较大小提供了“标杆”
比较和的大小.
【解】运用作差法:
2>0,
所以>
0是正数与负数的分界线,它为比较实数的大小提供了标杆.
如图是根据第24届国际数学家大会的会标设计的,会标灵感来源于中国古代数学家赵爽的弦图,图中有什么不等关系?
很显然赵爽弦图是我们在初中研究勾股定理时的模型,我们把它抽象成如图所示的图形.
设图中直角三角形的两个直角边长为,那么正方形的边长就是,这样,四个直角三角形的面积之和就是,正方形的面积为,很显然正方形的面积大于三角形面积和.即
当直角三角形变为等腰直角三角形时,内部的小正方形变成了一个点,此时,有,所以综合可知,
问题4:一个重要不等式
一般地,,这个不等式被称为重要不等式,
当且仅当时,等号成立.
事实上,利用完全平方公式也可以得到这个不等式:
因为,,当且仅当时,等号成立.
所以
因此,由两个实数大小关系的基本事实,我们得到:
,当且仅当时,等号成立.
问题4:一个重要不等式
★性质1【对称性】
★性质2【传递性】
★性质3【加减性】
★性质4【同乘性】
★性质5【同除性】
如果,那么
如果,,那么
如果,那么
如果,那么
如果,,那么
思考
请你先梳理等式的基本性质,再观察它们的共性.你能归纳一下发现等式基本性质的方法吗?
可以发现,性质1,2反映了相等关系自身的特性,性质3,4,5是从运算的角度提出的,反映了等式在运算中保持的不变性.
问题5:等式有什么性质
★性质1【对称性】
★性质2【传递性】
如果,那么.即
如果,,那么.
即,
我们来证明性质2:
类比等式的性质1,2,我们可以猜想不等式有如下性质:
问题6:不等式有什么性质
★性质3
【可加性】
★性质4
【可乘性】
★性质5
【同向可加性】
如果,那么
如果,,那么;
如果,,那么
不等式两边同时加上一个数,不变号
不等式两边同时乘上一个正数,不变号;
如果,,那么
不等式两边同时乘上一个负数,要变号 .
如果,,那么
如果,,那么
问题6:不等式有什么性质
类比等式的性质3~5,可以猜想不等式还有如下性质:
★性质6
【同向同正可乘性】
★性质7
【同正可乘方性】
如果, ,那么
如果,那么
等式
不等式
问题6:不等式有什么性质
我的等号左右能对应加减乘除(除数不为0),你行吗?
我只有同向可加性,同向可乘还必须保证是正数!
例2 已知,,求证
【分析】因为,所以要证,可先证明
【证明】因为,所以, .
所以 ,
因为,所以,即
>
<
<
<
习题2.1
(第42页)
2.某市环保局为增加城市的绿地面积,提出两个投资方案:方案A为一次性投资500万元;方案B为第一年投资100万元,以后每年投资10万元.列出不等式表示“经过n年之后,方案B的投入不少于方案A的投入” .
4.一个大于50且小于60的两位数,其个位数字比十位数字大2.试用不等式表示上述关系,并求这个两位数(用a和b分别表示这个两位数的十位数字和个位数字).
B
9.证明:圆的面积大于与它具有相同周长的正方形的面积.并据此说明,人们通常把自来水管的横截面制成圆形,而不是正方形的原因.
所以圆的面积更大
原因:自来水管的横截面是圆形的,可以最大面积地使水通过,减少阻力.
12.火车站有某公司代运的甲种货物1 530 ,乙种货物1 150 .现计划用A,B两种型号的货厢共50节运送这批货物.已知35甲种货物和15乙种货物可装满一节A型货厢,25甲种货物和35乙种货物可装满一节B型货厢,据此安排A,B两种货厢的节数,共有几种方案?若每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元,哪种方案的运费较少?
所以共有三种方案,方案一:安排A型货厢28节,B型货厢22节;方案二:安排A型货厢29节,B型货厢21节;方案三:安排A型货厢30节,B型货厢20节.
谢谢大家
We have many PowerPoint templates that has been specifically designed to help anyone that is stepping into the world of PowerPt for the very first time.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
