北师大版中考试题精选第二章二次函数的图像与性质
文档属性
| 名称 | 北师大版中考试题精选第二章二次函数的图像与性质 | 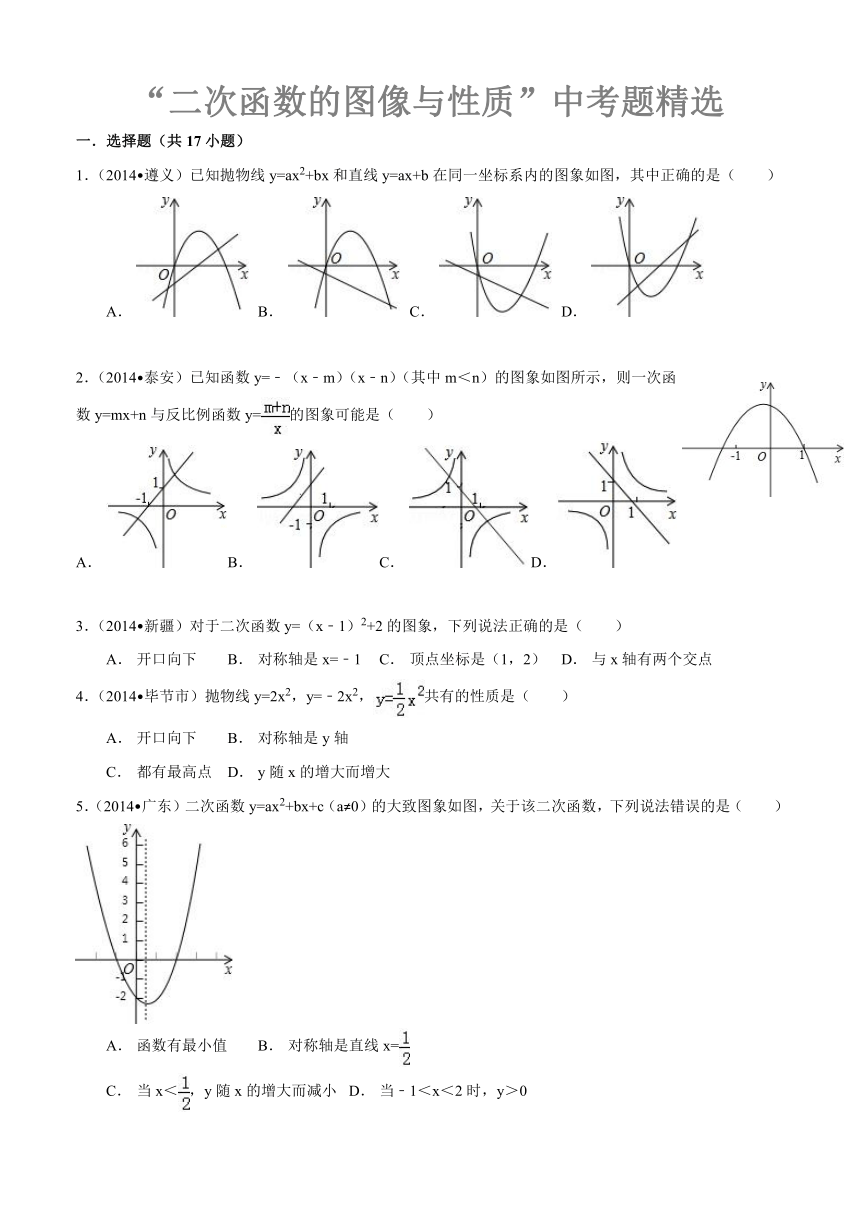 | |
| 格式 | zip | ||
| 文件大小 | 107.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-23 13:48:47 | ||
图片预览




文档简介
“二次函数的图像与性质”中考题精选
一.选择题(共17小题)
1.(2014 遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2014 泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.(2014 新疆)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A. 开口向下 B. 对称轴是x=﹣1 C. 顶点坐标是(1,2) D. 与x轴有两个交点
4.(2014 毕节市)抛物线y=2x2,y=﹣2x2,共有的性质是( )
A. 开口向下 B. 对称轴是y轴
C. 都有最高点 D. y随x的增大而增大
5.(2014 广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
( http: / / www.21cnjy.com )
A. 函数有最小值 B. 对称轴是直线x=
C. 当x<,y随x的增大而减小 D. 当﹣1<x<2时,y>0
6.(2014 淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A. 6 B. 5 C. 4 D. 3
7.(2014 三明)已知二次函数y=﹣x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A. b≥﹣1 B. b≤﹣1 C. b≥1 D. b≤1
8.(2014 兰州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
( http: / / www.21cnjy.com )
A. c>0 B. 2a+b=0 C. b2﹣4ac>0 D. a﹣b+c>0
9.(2014 达州)如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
( http: / / www.21cnjy.com )
A. ①② B. ①④ C. ①③④ D. ②③④
10.(2014 孝感)抛物线y=ax2 ( http: / / www.21cnjy.com )+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.
其中正确结论的个数为( )
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
11.(2013 陕西)已知两点A(﹣5, ( http: / / www.21cnjy.com )y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0,则x0的取值范围是( )
A. x0>﹣5 B. x0>﹣1 C. ﹣5<x0<﹣1 D. ﹣2<x0<3
12.(2012 泰安)设A(﹣2,y1) ( http: / / www.21cnjy.com ),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
13.(2014 牡丹江)将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
A. (0,2) B. (0,3) C. (0,4) D. (0,7)
14.(2014 荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A. y=(x﹣4)2﹣6 B. y=(x﹣4)2﹣2 C. y=(x﹣2)2﹣2 D. y=(x﹣1)2﹣3
15.(2014 丽水)在 ( http: / / www.21cnjy.com )同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A. (﹣3,﹣6) B. (1,﹣4) C. (1,﹣6) D. (﹣3,﹣4)
16.(2013 聊城)如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. 2 B. 4 C. 8 D. 16
17.(2013 衢州)抛物线y=x2 ( http: / / www.21cnjy.com )+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )
A. b=2,c=﹣6 B. b=2,c=0 C. b=﹣6,c=8 D. b=﹣6,c=2
二.填空题(共6小题)
18.(2014 珠海)如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 _________ .
( http: / / www.21cnjy.com )
19.(2014 牡丹江)抛物线y=ax2+bx+c经过点A(﹣3,0),对称轴是直线x=﹣1,则a+b+c= _________ .
20.(2014 乌鲁木齐)对于二次函数y=ax2﹣(2a﹣1)x+a﹣1(a≠0),有下列结论:
①其图象与x轴一定相交;
②若a<0,函数在x>1时,y随x的增大而减小;
③无论a取何值,抛物线的顶点始终在同一条直线上;
④无论a取何值,函数图象都经过同一个点.
其中所有正确的结论是 _________ .(填写正确结论的序号)
21.(2013 营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第 _________ 象限.
( http: / / www.21cnjy.com )
22.(2013 德阳)已知二次函 ( http: / / www.21cnjy.com )数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有
23.(2013 河南)如图,抛物 ( http: / / www.21cnjy.com )线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 _________ .
( http: / / www.21cnjy.com )
三.解答题(共4小题)
24.(2013 资阳)在关于x,y的二元一次方程组中.
(1)若a=3.求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值.
25.(2014 泉州)如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
( http: / / www.21cnjy.com )
26.(2012 柳州)已知:抛物线y=(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
27.(2014 绍兴)如果二次函数的二次项 ( http: / / www.21cnjy.com )系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
参考答案与试题解析
一.选择题(共17小题)
1. D.2. C.3. C.4. B.5. D.6. D.7. D.8. D.9. B.10. C.11. B.12. A.
13. B.14. B.15. C.16. B.17. B.
二.填空题(共6小题)
18.直线x=2.19. 0.20.①③④.21.四.22.①③④.23. 12.
三.解答题(共4小题)
24.解:(1)当a=3时,方程组为,
②×2得,4x﹣2y=2③,
①+③得,5x=5,
解得x=1,
把x=1代入①得,1+2y=3,
解得y=1,
所以,方程组的解是;
(2)方程组的两个方程相加得,3x+y=a+1,
所以,S=a(3x+y)=a(a+1)=(a+)2﹣,
所以,当a=﹣时,S有最小值﹣.
25.解:(1)∵二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
解得:h=1,a=﹣,
∴抛物线的对称轴为直线x=1;
(2)点A′是该函数图象的顶点.理由如下:
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,∠OA′B=30°,
∴OB=OA′=1,
∴A′B=OB=,
∴A′点的坐标为(1,),
∴点A′为抛物线y=﹣(x﹣1)2+的顶点.
( http: / / www.21cnjy.com )
26.解:(1)抛物线y=(x﹣1)2﹣3,
∵a=>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=>0,
∴函数y有最小值,最小值为﹣3;
(3)令x=0,则y=(0﹣1)2﹣3=﹣,
所以,点P的坐标为(0,﹣),
令y=0,则(x﹣1)2﹣3=0,
解得x1=﹣1,x2=3,
所以,点Q的坐标为(﹣1,0)或(3,0),
当点P(0,﹣),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
则,
解得,
所以直线PQ的解析式为y=﹣x﹣,
当P(0,﹣),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则,
解得,
所以,直线PQ的解析式为y=x﹣,
综上所述,直线PQ的解析式为y=﹣x﹣或y=x﹣.
27.解:(1)由题意可得出:y=x2﹣2x+1=(x﹣1)2,
∴此函数图象的顶点坐标为:(1,0);
(2)①由题意可得出:y=x2+4x﹣1=(x+2)2﹣5,
∴将此函数的图象先向右平移1个单位,再向上平移1个单位后得到:y=(x+2﹣1)2﹣5+1=(x+1)2﹣4=x2+2x﹣3,
∴图象对应的函数的特征数为:[2,﹣3];
②∵一个函数的特征数为[2,3],
∴函数解析式为:y=x2+2x+3=(x+1)2+2,
∵一个函数的特征数为[3,4],
∴函数解析式为:y=x2+3x+4=(x+)2+,
∴原函数的图象向左平移个单位,再向下平移个单位得到.
一.选择题(共17小题)
1.(2014 遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
2.(2014 泰安)已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
3.(2014 新疆)对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A. 开口向下 B. 对称轴是x=﹣1 C. 顶点坐标是(1,2) D. 与x轴有两个交点
4.(2014 毕节市)抛物线y=2x2,y=﹣2x2,共有的性质是( )
A. 开口向下 B. 对称轴是y轴
C. 都有最高点 D. y随x的增大而增大
5.(2014 广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
( http: / / www.21cnjy.com )
A. 函数有最小值 B. 对称轴是直线x=
C. 当x<,y随x的增大而减小 D. 当﹣1<x<2时,y>0
6.(2014 淄博)已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A. 6 B. 5 C. 4 D. 3
7.(2014 三明)已知二次函数y=﹣x2+2bx+c,当x>1时,y的值随x值的增大而减小,则实数b的取值范围是( )
A. b≥﹣1 B. b≤﹣1 C. b≥1 D. b≤1
8.(2014 兰州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( )
( http: / / www.21cnjy.com )
A. c>0 B. 2a+b=0 C. b2﹣4ac>0 D. a﹣b+c>0
9.(2014 达州)如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
( http: / / www.21cnjy.com )
A. ①② B. ①④ C. ①③④ D. ②③④
10.(2014 孝感)抛物线y=ax2 ( http: / / www.21cnjy.com )+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.
其中正确结论的个数为( )
( http: / / www.21cnjy.com )
A. 1个 B. 2个 C. 3个 D. 4个
11.(2013 陕西)已知两点A(﹣5, ( http: / / www.21cnjy.com )y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0,则x0的取值范围是( )
A. x0>﹣5 B. x0>﹣1 C. ﹣5<x0<﹣1 D. ﹣2<x0<3
12.(2012 泰安)设A(﹣2,y1) ( http: / / www.21cnjy.com ),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
13.(2014 牡丹江)将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( )
A. (0,2) B. (0,3) C. (0,4) D. (0,7)
14.(2014 荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A. y=(x﹣4)2﹣6 B. y=(x﹣4)2﹣2 C. y=(x﹣2)2﹣2 D. y=(x﹣1)2﹣3
15.(2014 丽水)在 ( http: / / www.21cnjy.com )同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )
A. (﹣3,﹣6) B. (1,﹣4) C. (1,﹣6) D. (﹣3,﹣4)
16.(2013 聊城)如图,在平面直角坐标系中,抛物线y=经过平移得到抛物线y=,其对称轴与两段抛物线所围成的阴影部分的面积为( )
( http: / / www.21cnjy.com )
A. 2 B. 4 C. 8 D. 16
17.(2013 衢州)抛物线y=x2 ( http: / / www.21cnjy.com )+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )
A. b=2,c=﹣6 B. b=2,c=0 C. b=﹣6,c=8 D. b=﹣6,c=2
二.填空题(共6小题)
18.(2014 珠海)如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 _________ .
( http: / / www.21cnjy.com )
19.(2014 牡丹江)抛物线y=ax2+bx+c经过点A(﹣3,0),对称轴是直线x=﹣1,则a+b+c= _________ .
20.(2014 乌鲁木齐)对于二次函数y=ax2﹣(2a﹣1)x+a﹣1(a≠0),有下列结论:
①其图象与x轴一定相交;
②若a<0,函数在x>1时,y随x的增大而减小;
③无论a取何值,抛物线的顶点始终在同一条直线上;
④无论a取何值,函数图象都经过同一个点.
其中所有正确的结论是 _________ .(填写正确结论的序号)
21.(2013 营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第 _________ 象限.
( http: / / www.21cnjy.com )
22.(2013 德阳)已知二次函 ( http: / / www.21cnjy.com )数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有
23.(2013 河南)如图,抛物 ( http: / / www.21cnjy.com )线的顶点为P(﹣2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 _________ .
( http: / / www.21cnjy.com )
三.解答题(共4小题)
24.(2013 资阳)在关于x,y的二元一次方程组中.
(1)若a=3.求方程组的解;
(2)若S=a(3x+y),当a为何值时,S有最值.
25.(2014 泉州)如图,已知二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
( http: / / www.21cnjy.com )
26.(2012 柳州)已知:抛物线y=(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
27.(2014 绍兴)如果二次函数的二次项 ( http: / / www.21cnjy.com )系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[﹣2,1],求此函数图象的顶点坐标.
(2)探究下列问题:
①若一个函数的特征数为[4,﹣1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
参考答案与试题解析
一.选择题(共17小题)
1. D.2. C.3. C.4. B.5. D.6. D.7. D.8. D.9. B.10. C.11. B.12. A.
13. B.14. B.15. C.16. B.17. B.
二.填空题(共6小题)
18.直线x=2.19. 0.20.①③④.21.四.22.①③④.23. 12.
三.解答题(共4小题)
24.解:(1)当a=3时,方程组为,
②×2得,4x﹣2y=2③,
①+③得,5x=5,
解得x=1,
把x=1代入①得,1+2y=3,
解得y=1,
所以,方程组的解是;
(2)方程组的两个方程相加得,3x+y=a+1,
所以,S=a(3x+y)=a(a+1)=(a+)2﹣,
所以,当a=﹣时,S有最小值﹣.
25.解:(1)∵二次函数y=a(x﹣h)2+的图象经过原点O(0,0),A(2,0).
解得:h=1,a=﹣,
∴抛物线的对称轴为直线x=1;
(2)点A′是该函数图象的顶点.理由如下:
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,∠OA′B=30°,
∴OB=OA′=1,
∴A′B=OB=,
∴A′点的坐标为(1,),
∴点A′为抛物线y=﹣(x﹣1)2+的顶点.
( http: / / www.21cnjy.com )
26.解:(1)抛物线y=(x﹣1)2﹣3,
∵a=>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=>0,
∴函数y有最小值,最小值为﹣3;
(3)令x=0,则y=(0﹣1)2﹣3=﹣,
所以,点P的坐标为(0,﹣),
令y=0,则(x﹣1)2﹣3=0,
解得x1=﹣1,x2=3,
所以,点Q的坐标为(﹣1,0)或(3,0),
当点P(0,﹣),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
则,
解得,
所以直线PQ的解析式为y=﹣x﹣,
当P(0,﹣),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则,
解得,
所以,直线PQ的解析式为y=x﹣,
综上所述,直线PQ的解析式为y=﹣x﹣或y=x﹣.
27.解:(1)由题意可得出:y=x2﹣2x+1=(x﹣1)2,
∴此函数图象的顶点坐标为:(1,0);
(2)①由题意可得出:y=x2+4x﹣1=(x+2)2﹣5,
∴将此函数的图象先向右平移1个单位,再向上平移1个单位后得到:y=(x+2﹣1)2﹣5+1=(x+1)2﹣4=x2+2x﹣3,
∴图象对应的函数的特征数为:[2,﹣3];
②∵一个函数的特征数为[2,3],
∴函数解析式为:y=x2+2x+3=(x+1)2+2,
∵一个函数的特征数为[3,4],
∴函数解析式为:y=x2+3x+4=(x+)2+,
∴原函数的图象向左平移个单位,再向下平移个单位得到.
