6.2三角形的面积(教案)-五年级上册上册数学 人教版
文档属性
| 名称 | 6.2三角形的面积(教案)-五年级上册上册数学 人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 00:00:00 | ||
图片预览



文档简介
《三角形的面积》教学设计
备教材内容
1.本课时教学的是教材91~92页的内容。
2.教材以实际问题“怎样算出红领巾的面积呢?”为载体,先以小组合作学习的形式把三角形转化成学过的图形,再让学生通过动手操作和观察探究,推导出三角形的面积计算公式,最后用字母表示出面积计算公式。例2是应用三角形的面积计算公式解决实际问题。
3.三角形面积计算公式的推导,一方面,以实际问题“怎样计算红领巾的面积”为载体,以小组合作学习的形式展现学生探索交流的过程,呈现学生操作活动的多样性。通过观察思考“你发现了什么”,使探究过程更加明确。另一方面,根据平行四边形面积公式推导的方法提出解决问题的思路:把三角形也转化成学过的图形;通过学生动手操作和实验,发现三角形与平行四边形的关系,推导出三角形面积计算公式。这里给出三角形与平行四边形的转化示意图,有利于学生观察它们之间的关系,自主探索三角形面积公式。最后和平行四边形一样,结合三角形的图形,用字母表示出三角形的面积计算公式。将三角形转化成已学过的图形,教材没有呈现割补方法,而是用两个同样三角形拼摆的方法这种方法推导过程简单,学生比较容易理解和掌握。
4.三角形面积的计算是在学生掌握了长方形、正方形和平行四边形面积计算的基础上进行教学的,三角形面积的计算是小学阶段学习几何知识的重要内容,也是学生今后学习几何知识的重要基础。
备教法学法
学生已经掌握了三角形的特征以及长方形、正方形、平行四边形的面积计算方法和转化的策略,教师可以在此基础上,先放手让学生自主探究,继续渗透转化思想,让学生经历将未知转化为已知的过程,也就是把三角形转化为已经知道面积计算公式的图形,再推导出三角形的面积计算公式。引导学生发现两个完全一样的三角形可以拼成一个平行四边形,明确三角形的面积是拼成的平行四边形面积的一半,掌握三角形的面积计算公式。提高学生的动手操作能力及实践能力。继续渗透“转化”的思想。有了推导平行四边形面积计算公式的经
验,这里可以放手让学生自主探究。继续渗透转化思想,让学生经历将未知转化为已知的过
程,也就是把三角形转化为已经知道面积计算公式的图形,就能推导出三角形的面积公式。
准备相同的直角三角形、锐角三角形、钝角三角形各两个,放手让学生动手操作将三角形转化成学过的图形。学生可能会拼出多种不同形状的图形,但只有拼成长方形和平行四边形才能推导出三角形的面积。让学生通过交流发现:任意两个完全相同的三角形都可以拼成
一个平行四边形。再结合三角形转化成平行四边形的示意图引导学生自主推导公式。强调公式中的“÷2”。计算三角形面积时,学生经常忘记除以2,教学中要引导学生加深理解。从拼摆开始,就让学生明确用两个相同的三角形拼成的图形,三角形的面积是这个图形的一半。推导公式时,让学生思考:三角形的底乘高计算的是哪个图形的面积?从反面提醒学生记住“除以2”适当拓展。根据学生的实际情况,适当拓展割补的推导方法。
备教学目标
1.经历操作、观察、比较、归纳等过程,推导并掌握三角形的面积计算公式,进一步体会转化思想,培养推理意识。
2.会计算三角形的面积,并能应用三角形的面积计算公式解决简单的实际问题。
3.获得积极的情感体验,培养学习数学的兴趣。
备教学重难点
重点:掌握三角形的面积计算公式,会计算三角形的面积。
难点:理解拼成的平行四边形和原来的三角形之间的关系。
备已学知识
长方形的面积=长×宽 用字母表示:S=ab
正方形的面积=边长×边长 用字母表示:S=a2
平行四边形的面积=底×高 用字母表示:S=ah
备知识讲解
知识点一 三角形的面积计算公式
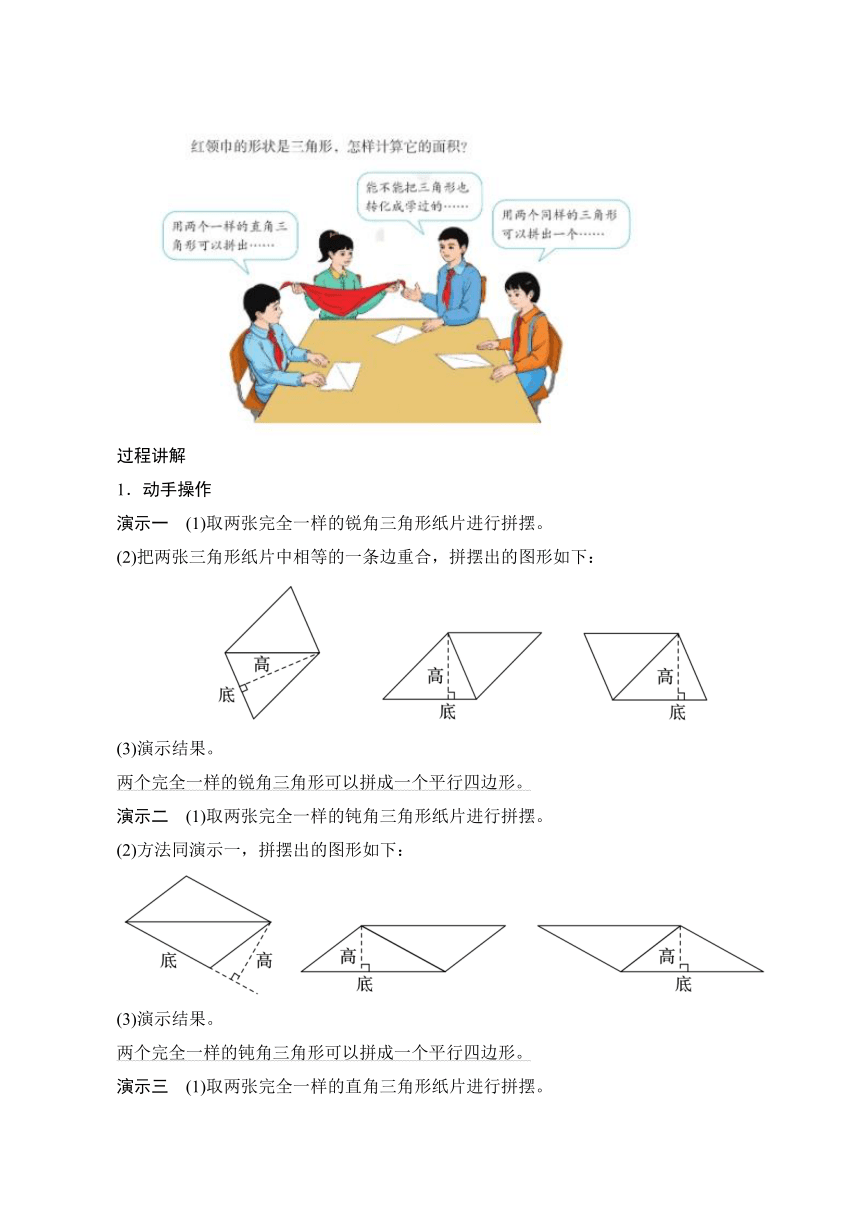
问题导入 怎样计算三角形的面积呢?在求三角形的面积时是否可以把三角形转化成学过的图形呢?(教材91页)
过程讲解
1.动手操作
演示一 (1)取两张完全一样的锐角三角形纸片进行拼摆。
(2)把两张三角形纸片中相等的一条边重合,拼摆出的图形如下:
(3)演示结果。
两个完全一样的锐角三角形可以拼成一个平行四边形。
演示二 (1)取两张完全一样的钝角三角形纸片进行拼摆。
(2)方法同演示一,拼摆出的图形如下:
(3)演示结果。
两个完全一样的钝角三角形可以拼成一个平行四边形。
演示三 (1)取两张完全一样的直角三角形纸片进行拼摆。
(2)方法同演示一,拼摆出的图形如下:
(3)演示结果。
两个完全一样的直角三角形可以拼成一个平行四边形或一个长方形。
2.根据平行四边形的面积计算公式推导三角形的面积计算公式
(1)观察三角形和拼成的平行四边形,找出两者之间的联系。
①拼成的平行四边形的底等于三角形的底。
②拼成的平行四边形的高等于三角形的高。
③拼成的平行四边形的面积等于三角形面积的2倍,也就是说每个三角形的面积等于拼成的平行四边形面积的一半。
(2)推导三角形的面积计算公式。
平行四边形的面积=底×高
三角形的面积×2=底 × 高
由此可知:三角形的面积=底×高÷2
3.根据长方形的面积计算公式推导三角形的面积计算公式
(1)观察三角形和拼成的长方形,找出两者之间的联系。
①拼成的长方形的长等于三角形的底。
②拼成的长方形的宽等于三角形的高。
③拼成的长方形的面积等于三角形面积的2倍,也就是说每个三角形的面积等于拼成的长方形面积的一半。
(2)推导三角形的面积计算公式。
思想方法提示 把三角形转化成平行四边形或长方形,进而推导出三角形的面积计算公式,体现了转化的思想方法。
长方形的面积 =长×宽
三角形的面积×2 =底×高
由此可知:三角形的面积=底×高÷2
4.构建三角形面积的计算模型
如果用S表示三角形的面积,用a和h分别表示三角形的底和高,那么三角形的面积计算公式可以写成:S=ah÷2。
归纳总结
三角形的面积计算公式:三角形的面积=底×高÷2,用字母表示为S=ah÷2。
拓展提高
运用割补法、折叠法也可以推导出三角形的面积计算公式。
1.割补法。
(1)三角形的面积=拼成的平行四边形的面积
(2)拼成的平行四边形的底等于三角形的底,高等于三角形高的一半。
由此可知:拼成的平行四边形的面积=三角形的底×(三角形的高÷2)
由此推出:三角形的面积=底×高÷2
2.折叠法。
(1)折叠后的长方形的面积是三角形面积的一半。
(2)折叠后的长方形的长等于三角形底的一半,宽等于三角形高的一半。
由此可知:折叠后的长方形的面积=(三角形的底÷2)×(三角形的高÷2)
由此推出:三角形的面积=折叠后的长方形的面积×2=(底÷2)×(高÷2)×2=底×高÷2
知识点二 三角形面积计算公式的应用
应用一 已知三角形的底和高,求三角形的面积。
典型例题 红领巾的底是100cm,高33cm,它的面积是多少平方厘米?(教材92页例2)
思路分析 要求红领巾的面积,就是求三角形的面积。已知三角形的底和高,要求三角形的面积,可以直接运用三角形的面积计算公式求得。
正确解答
S=ah÷2
=100×33÷2
=1650(cm2)
答:它的面积是1650cm2。
方法总结
已知三角形的底和高,可以直接运用三角形的面积计算公式S=ah÷2求出三角形的面积。
应用二 已知三角形的面积和底(或高),求高(或底)。
典型例题 一块三角形绿地的面积是13.5m2,底是6m,高是多少米?
思路分析 可以先根据三角形的面积计算公式S=ah÷2推导出h=2S÷a,再计算。
正确解答
由S=ah÷2推导出h=2S÷a。
h=2S÷a
=2×13.5÷6
=4.5(m)
答:高是4.5m。
方法总结
已知三角形的面积和高,求底,可以根据a=2S÷h计算;已知三角形的面积和底,求高,可以根据h=2S÷a计算。
知识巧记
计算三角形面积,底高之积除以2。
面积乘2除以底,轻松求高很容易。
面积乘2除以高,底的数据就出现。
解决问题要注意,数2千万别忘记。
备易错易混
误区一 判断:三角形的面积等于平行四边形面积的一半。(√)
错解分析 此题错在没有强调三角形的底和高与平行四边形的底和高分别相等这一条件。
错解改正 ×
温馨提示
三角形的面积等于与它等底等高的平行四边形面积的一半。
误区二 判断:三角形的底是8cm,高是4cm,面积是32cm2。(√)
错解分析 此题错在三角形的面积计算公式运用错误,忘记除以2了。
错解改正 ×
温馨提示
计算三角形的面积时,不要忘记底乘高后再除以2。
误区三 一个三角形的面积是75cm2,高是7.5cm,它的底是多少厘米?
75÷7.5=10(cm)
答:它的底是10cm。
错解分析 此题错在已知三角形的面积和高,求底时直接用面积除以高了,忘记要先用面积乘2了。
错解改正 75×2÷7.5=20(cm)
答:它的底是20cm。
温馨提示
已知三角形的面积和高,求底时一定要用三角形的面积先乘2再计算。
备综合能力
综合运用 运用平行四边形与三角形面积之间的关系解决图形面积的问题
典型例题 下图中阴影部分的面积是10cm2,平行四边形ABCD的面积是多少平方厘米?
思路分析 图中的阴影部分是一个三角形,已知它的面积和底,根据三角形的面积计算公式S=ah÷2推导出h=2S÷a,可求出它的高。这个高也是平行四边形ABCD的高,根据平行四边形的面积计算公式可求出它的面积。
正确解答 10×2÷4=5(cm)
(6+4)×5=50(cm2)
答:平行四边形ABCD的面积是50cm2。
方法总结
在平行四边形中,底与平行四边形的底在同一条边上且顶点在对边上的三角形的高与平行四边形的高相等。
思维开放 运用剔除法或分割法解决图形面积的问题
典型例题 右图中两个正方形的边长分别是8cm和4cm,求阴影部分的面积。
思路分析
思路一 剔除法。
先求出两个正方形的面积和,再从中减去空白部分的面积和,即可求出阴影部分的面积。
思路二 分割法。
将阴影部分分割成两个已知底和高的三角形,如下图。先分别求出两个阴影三角形的面积,再求出整个阴影部分的面积。
正确解答
方法一 4×4+8×8=80(cm2)
4×(4+8)÷2+8×8÷2=56(cm2)
80-56=24(cm2)
方法二 4×4÷2+(8-4)×8÷2
=8+16
=24(cm2)
答:阴影部分的面积是24cm2。
方法总结
求图形的面积有多种方法。如果阴影部分的面积不能直接求出来,那么可以从整个图形中剔除空白部分的面积,求出阴影部分的面积;也可以先将阴影部分分割成几个基本图形,再求这几个基本图形的面积和。
备教学资源
加菲尔德证明勾股定理的故事
勾股定理指的是在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方。勾股定理在中国古代被称为“商高定理”,在有些国家被称为“毕达哥拉斯定理”。
1876年,美国华盛顿的郊外,加菲尔德正在散步,欣赏着周围美丽的风景。突然,他发现在路边有两个小孩儿正在争论着什么。他走过去静静地看着,只见其中一个小孩儿用树枝在地上画了一个直角三角形。于是,加菲尔德便开口问道:“小朋友,你们在干什么?”画直角三角形的小孩儿回答说:“先生,你知道勾股定理吗?如果一个直角三角形的两条直角边长分别是3和4,那么它的斜边长又是多少呢?”加菲尔德回答道:“斜边长是5啊!”另外一个小孩儿接着问道:“如果一个直角三角形的两条直角边长分别是4和5,那么它的斜边长又是多少呢?”加菲尔德不假思索地答道:“斜边长的平方等于4的平方加上5的平方啊。”小孩儿接着又问道:“这是为什么呢?先生你能说出其中的道理吗?”
加菲尔德愣住了,因为他从来没有思索过勾股定理的证明过程。
回到家后,加菲尔德便开始思考小孩儿留给他的问题。经过反复的计算和推演,他终于弄清楚了小孩儿留给他的“难题”,并得出了比较简便的证明过程。
在上图中,利用梯形的面积等于三个直角三角形面积的和,化简整理可以得出勾股定理。
科学之祖——泰勒斯
泰勒斯被称为“科学之祖”,他是古希腊第一个自然科学家。他把埃及的地面几何演变成平面几何学,并发现了许多几何学的基本定理,如“等腰三角形底角相等”“相似三角形对应边成比例”等,并将几何学知识应用到了实践中。
备教材内容
1.本课时教学的是教材91~92页的内容。
2.教材以实际问题“怎样算出红领巾的面积呢?”为载体,先以小组合作学习的形式把三角形转化成学过的图形,再让学生通过动手操作和观察探究,推导出三角形的面积计算公式,最后用字母表示出面积计算公式。例2是应用三角形的面积计算公式解决实际问题。
3.三角形面积计算公式的推导,一方面,以实际问题“怎样计算红领巾的面积”为载体,以小组合作学习的形式展现学生探索交流的过程,呈现学生操作活动的多样性。通过观察思考“你发现了什么”,使探究过程更加明确。另一方面,根据平行四边形面积公式推导的方法提出解决问题的思路:把三角形也转化成学过的图形;通过学生动手操作和实验,发现三角形与平行四边形的关系,推导出三角形面积计算公式。这里给出三角形与平行四边形的转化示意图,有利于学生观察它们之间的关系,自主探索三角形面积公式。最后和平行四边形一样,结合三角形的图形,用字母表示出三角形的面积计算公式。将三角形转化成已学过的图形,教材没有呈现割补方法,而是用两个同样三角形拼摆的方法这种方法推导过程简单,学生比较容易理解和掌握。
4.三角形面积的计算是在学生掌握了长方形、正方形和平行四边形面积计算的基础上进行教学的,三角形面积的计算是小学阶段学习几何知识的重要内容,也是学生今后学习几何知识的重要基础。
备教法学法
学生已经掌握了三角形的特征以及长方形、正方形、平行四边形的面积计算方法和转化的策略,教师可以在此基础上,先放手让学生自主探究,继续渗透转化思想,让学生经历将未知转化为已知的过程,也就是把三角形转化为已经知道面积计算公式的图形,再推导出三角形的面积计算公式。引导学生发现两个完全一样的三角形可以拼成一个平行四边形,明确三角形的面积是拼成的平行四边形面积的一半,掌握三角形的面积计算公式。提高学生的动手操作能力及实践能力。继续渗透“转化”的思想。有了推导平行四边形面积计算公式的经
验,这里可以放手让学生自主探究。继续渗透转化思想,让学生经历将未知转化为已知的过
程,也就是把三角形转化为已经知道面积计算公式的图形,就能推导出三角形的面积公式。
准备相同的直角三角形、锐角三角形、钝角三角形各两个,放手让学生动手操作将三角形转化成学过的图形。学生可能会拼出多种不同形状的图形,但只有拼成长方形和平行四边形才能推导出三角形的面积。让学生通过交流发现:任意两个完全相同的三角形都可以拼成
一个平行四边形。再结合三角形转化成平行四边形的示意图引导学生自主推导公式。强调公式中的“÷2”。计算三角形面积时,学生经常忘记除以2,教学中要引导学生加深理解。从拼摆开始,就让学生明确用两个相同的三角形拼成的图形,三角形的面积是这个图形的一半。推导公式时,让学生思考:三角形的底乘高计算的是哪个图形的面积?从反面提醒学生记住“除以2”适当拓展。根据学生的实际情况,适当拓展割补的推导方法。
备教学目标
1.经历操作、观察、比较、归纳等过程,推导并掌握三角形的面积计算公式,进一步体会转化思想,培养推理意识。
2.会计算三角形的面积,并能应用三角形的面积计算公式解决简单的实际问题。
3.获得积极的情感体验,培养学习数学的兴趣。
备教学重难点
重点:掌握三角形的面积计算公式,会计算三角形的面积。
难点:理解拼成的平行四边形和原来的三角形之间的关系。
备已学知识
长方形的面积=长×宽 用字母表示:S=ab
正方形的面积=边长×边长 用字母表示:S=a2
平行四边形的面积=底×高 用字母表示:S=ah
备知识讲解
知识点一 三角形的面积计算公式
问题导入 怎样计算三角形的面积呢?在求三角形的面积时是否可以把三角形转化成学过的图形呢?(教材91页)
过程讲解
1.动手操作
演示一 (1)取两张完全一样的锐角三角形纸片进行拼摆。
(2)把两张三角形纸片中相等的一条边重合,拼摆出的图形如下:
(3)演示结果。
两个完全一样的锐角三角形可以拼成一个平行四边形。
演示二 (1)取两张完全一样的钝角三角形纸片进行拼摆。
(2)方法同演示一,拼摆出的图形如下:
(3)演示结果。
两个完全一样的钝角三角形可以拼成一个平行四边形。
演示三 (1)取两张完全一样的直角三角形纸片进行拼摆。
(2)方法同演示一,拼摆出的图形如下:
(3)演示结果。
两个完全一样的直角三角形可以拼成一个平行四边形或一个长方形。
2.根据平行四边形的面积计算公式推导三角形的面积计算公式
(1)观察三角形和拼成的平行四边形,找出两者之间的联系。
①拼成的平行四边形的底等于三角形的底。
②拼成的平行四边形的高等于三角形的高。
③拼成的平行四边形的面积等于三角形面积的2倍,也就是说每个三角形的面积等于拼成的平行四边形面积的一半。
(2)推导三角形的面积计算公式。
平行四边形的面积=底×高
三角形的面积×2=底 × 高
由此可知:三角形的面积=底×高÷2
3.根据长方形的面积计算公式推导三角形的面积计算公式
(1)观察三角形和拼成的长方形,找出两者之间的联系。
①拼成的长方形的长等于三角形的底。
②拼成的长方形的宽等于三角形的高。
③拼成的长方形的面积等于三角形面积的2倍,也就是说每个三角形的面积等于拼成的长方形面积的一半。
(2)推导三角形的面积计算公式。
思想方法提示 把三角形转化成平行四边形或长方形,进而推导出三角形的面积计算公式,体现了转化的思想方法。
长方形的面积 =长×宽
三角形的面积×2 =底×高
由此可知:三角形的面积=底×高÷2
4.构建三角形面积的计算模型
如果用S表示三角形的面积,用a和h分别表示三角形的底和高,那么三角形的面积计算公式可以写成:S=ah÷2。
归纳总结
三角形的面积计算公式:三角形的面积=底×高÷2,用字母表示为S=ah÷2。
拓展提高
运用割补法、折叠法也可以推导出三角形的面积计算公式。
1.割补法。
(1)三角形的面积=拼成的平行四边形的面积
(2)拼成的平行四边形的底等于三角形的底,高等于三角形高的一半。
由此可知:拼成的平行四边形的面积=三角形的底×(三角形的高÷2)
由此推出:三角形的面积=底×高÷2
2.折叠法。
(1)折叠后的长方形的面积是三角形面积的一半。
(2)折叠后的长方形的长等于三角形底的一半,宽等于三角形高的一半。
由此可知:折叠后的长方形的面积=(三角形的底÷2)×(三角形的高÷2)
由此推出:三角形的面积=折叠后的长方形的面积×2=(底÷2)×(高÷2)×2=底×高÷2
知识点二 三角形面积计算公式的应用
应用一 已知三角形的底和高,求三角形的面积。
典型例题 红领巾的底是100cm,高33cm,它的面积是多少平方厘米?(教材92页例2)
思路分析 要求红领巾的面积,就是求三角形的面积。已知三角形的底和高,要求三角形的面积,可以直接运用三角形的面积计算公式求得。
正确解答
S=ah÷2
=100×33÷2
=1650(cm2)
答:它的面积是1650cm2。
方法总结
已知三角形的底和高,可以直接运用三角形的面积计算公式S=ah÷2求出三角形的面积。
应用二 已知三角形的面积和底(或高),求高(或底)。
典型例题 一块三角形绿地的面积是13.5m2,底是6m,高是多少米?
思路分析 可以先根据三角形的面积计算公式S=ah÷2推导出h=2S÷a,再计算。
正确解答
由S=ah÷2推导出h=2S÷a。
h=2S÷a
=2×13.5÷6
=4.5(m)
答:高是4.5m。
方法总结
已知三角形的面积和高,求底,可以根据a=2S÷h计算;已知三角形的面积和底,求高,可以根据h=2S÷a计算。
知识巧记
计算三角形面积,底高之积除以2。
面积乘2除以底,轻松求高很容易。
面积乘2除以高,底的数据就出现。
解决问题要注意,数2千万别忘记。
备易错易混
误区一 判断:三角形的面积等于平行四边形面积的一半。(√)
错解分析 此题错在没有强调三角形的底和高与平行四边形的底和高分别相等这一条件。
错解改正 ×
温馨提示
三角形的面积等于与它等底等高的平行四边形面积的一半。
误区二 判断:三角形的底是8cm,高是4cm,面积是32cm2。(√)
错解分析 此题错在三角形的面积计算公式运用错误,忘记除以2了。
错解改正 ×
温馨提示
计算三角形的面积时,不要忘记底乘高后再除以2。
误区三 一个三角形的面积是75cm2,高是7.5cm,它的底是多少厘米?
75÷7.5=10(cm)
答:它的底是10cm。
错解分析 此题错在已知三角形的面积和高,求底时直接用面积除以高了,忘记要先用面积乘2了。
错解改正 75×2÷7.5=20(cm)
答:它的底是20cm。
温馨提示
已知三角形的面积和高,求底时一定要用三角形的面积先乘2再计算。
备综合能力
综合运用 运用平行四边形与三角形面积之间的关系解决图形面积的问题
典型例题 下图中阴影部分的面积是10cm2,平行四边形ABCD的面积是多少平方厘米?
思路分析 图中的阴影部分是一个三角形,已知它的面积和底,根据三角形的面积计算公式S=ah÷2推导出h=2S÷a,可求出它的高。这个高也是平行四边形ABCD的高,根据平行四边形的面积计算公式可求出它的面积。
正确解答 10×2÷4=5(cm)
(6+4)×5=50(cm2)
答:平行四边形ABCD的面积是50cm2。
方法总结
在平行四边形中,底与平行四边形的底在同一条边上且顶点在对边上的三角形的高与平行四边形的高相等。
思维开放 运用剔除法或分割法解决图形面积的问题
典型例题 右图中两个正方形的边长分别是8cm和4cm,求阴影部分的面积。
思路分析
思路一 剔除法。
先求出两个正方形的面积和,再从中减去空白部分的面积和,即可求出阴影部分的面积。
思路二 分割法。
将阴影部分分割成两个已知底和高的三角形,如下图。先分别求出两个阴影三角形的面积,再求出整个阴影部分的面积。
正确解答
方法一 4×4+8×8=80(cm2)
4×(4+8)÷2+8×8÷2=56(cm2)
80-56=24(cm2)
方法二 4×4÷2+(8-4)×8÷2
=8+16
=24(cm2)
答:阴影部分的面积是24cm2。
方法总结
求图形的面积有多种方法。如果阴影部分的面积不能直接求出来,那么可以从整个图形中剔除空白部分的面积,求出阴影部分的面积;也可以先将阴影部分分割成几个基本图形,再求这几个基本图形的面积和。
备教学资源
加菲尔德证明勾股定理的故事
勾股定理指的是在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方。勾股定理在中国古代被称为“商高定理”,在有些国家被称为“毕达哥拉斯定理”。
1876年,美国华盛顿的郊外,加菲尔德正在散步,欣赏着周围美丽的风景。突然,他发现在路边有两个小孩儿正在争论着什么。他走过去静静地看着,只见其中一个小孩儿用树枝在地上画了一个直角三角形。于是,加菲尔德便开口问道:“小朋友,你们在干什么?”画直角三角形的小孩儿回答说:“先生,你知道勾股定理吗?如果一个直角三角形的两条直角边长分别是3和4,那么它的斜边长又是多少呢?”加菲尔德回答道:“斜边长是5啊!”另外一个小孩儿接着问道:“如果一个直角三角形的两条直角边长分别是4和5,那么它的斜边长又是多少呢?”加菲尔德不假思索地答道:“斜边长的平方等于4的平方加上5的平方啊。”小孩儿接着又问道:“这是为什么呢?先生你能说出其中的道理吗?”
加菲尔德愣住了,因为他从来没有思索过勾股定理的证明过程。
回到家后,加菲尔德便开始思考小孩儿留给他的问题。经过反复的计算和推演,他终于弄清楚了小孩儿留给他的“难题”,并得出了比较简便的证明过程。
在上图中,利用梯形的面积等于三个直角三角形面积的和,化简整理可以得出勾股定理。
科学之祖——泰勒斯
泰勒斯被称为“科学之祖”,他是古希腊第一个自然科学家。他把埃及的地面几何演变成平面几何学,并发现了许多几何学的基本定理,如“等腰三角形底角相等”“相似三角形对应边成比例”等,并将几何学知识应用到了实践中。
