2023-2024学年九年级上册数学冀教版 第二十三章《数据分析》单元检测题(含答案)
文档属性
| 名称 | 2023-2024学年九年级上册数学冀教版 第二十三章《数据分析》单元检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 10:59:52 | ||
图片预览



文档简介
第二十三章《数据分析》单元检测题
2023-2024学年九年级上册数学冀教版
一、单选题(本大题共12小题,每小题3分,共36分)
1.近几年受新冠肺炎病毒影响,多地学校开展停课不停学网上教学活动,梁老师调查统计了本班40名学生一天利用网课学习的时间(单位:小时)如表:
时间(小时) 3小时或以下 4 5 6 7 8小时或以上
人数(个) 4 6 20 5 3 2
这组数据的众数是( )
A.5 B.6 C.8 D.20
2.清溪中学在劳动基地开展主题为“春种秋收”的劳动教育活动,九年级(1)班师生共参与了剪枝、锄地、除草、浇水、施肥五项实践活动,已知五个项目的参与人数分别是,则这组数据的众数和中位数分别是( )
A.11,9 B.10,9 C.10,11 D.11,11
3.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A.160 B.165 C.170 D.175
4.一个射手连续射靶10次,其中3次射中10环,3次射中9环,4次射中8环.则该射手射中环数的中位数和众数分别为( )
A.8,9 B.9,8 C.8.5,8 D.8.5,9
5.五个绿化小组一天植树的棵树如下:10、10、12、、8.已知这组数据的众数与平均数相同,那么这组数据的平均数是( )
A.12 B.10 C.8 D.9
6.在庆祝中国共产党成立100周年的校园歌唱比赛中,15名参赛同学的成绩各不相同,按照成绩取前7名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这15名同学成绩的( )
A.中位数 B.众数 C.平均数 D.方差
7.为了推选一名同学参加学校举办的“中国汉字听写大赛”,九(3)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.8,根据以上数据,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
8.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数x与方差s2如下表所示:
甲 乙 丙 丁
平均数 8.0 8.0 8.5 8.5
方差s2 3.5 15.5 3.5 16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
9.A、B、C、D、E五名射击运动员在一次比赛中的平均成绩是80环,而A、B、C三人的平均成绩是78环,那么下列说法中一定正确的是( )
A.D、E的成绩比其他三人好
B.B、E两人的平均成绩是83环
C.最高分得主不是A、B、C
D.D、E中至少有1人的成绩不少于83环.
10.为庆祝2023年5月30日神舟十六号成功发射,学校开展航天知识竞赛活动,经过几轮筛选,某班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经统计,四名同学成绩的平均数(单位:分)及方差(单位:分)如下表:
甲 乙 丙 丁
平均数 97 95 97 93
方差 0.3 1.2 1.3 0.6
根据表中数据,要选一名成绩好且状态稳定的同学参赛,应选择( )
A.甲 B.乙 C.丙 D.丁
11.下表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分与方差∶
甲 乙 丙 丁
平均分 93 96 96 93
方差 5.1 5.1 1.2 1.2
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
12.下列说法正确的是( )
A.在小明,小红,小月三人中抽2人参加比赛,小刚被轴中是随机事件
B.要了解学校2000学生的体质健康情况,随机抽取100名学生进行调查,在该调查中样本容量是100名学生
C.预防“新冠病毒”期间,有关部门对某商店在售口罩的合格情况进行抽检,抽检了20包口罩,其中18包合格,该商店共进货100包,估计合格的口罩约有90包
D.了解某班学生的身高情况适宜抽样调查
二、填空题(本大题共8小题,每小题3分,共24分)
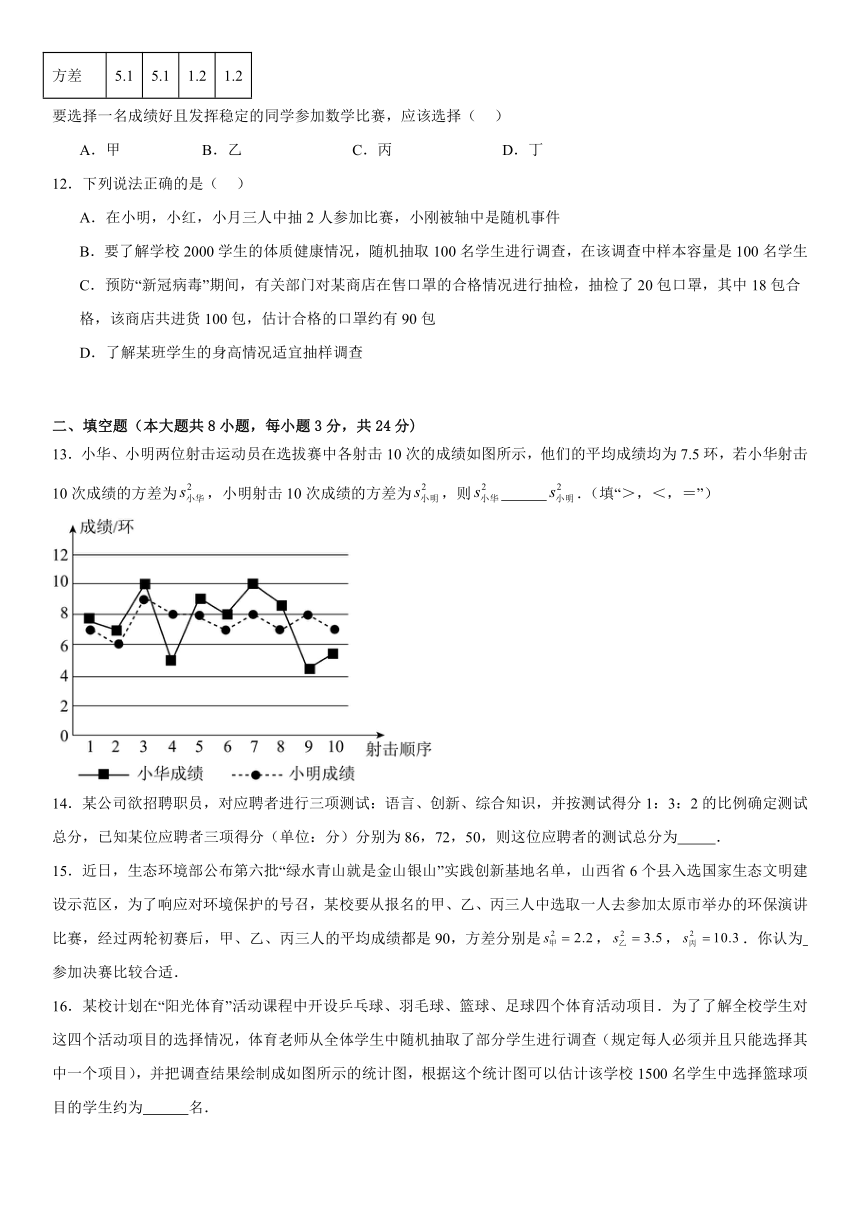
13.小华、小明两位射击运动员在选拔赛中各射击10次的成绩如图所示,他们的平均成绩均为7.5环,若小华射击10次成绩的方差为,小明射击10次成绩的方差为,则 .(填“>,<,=”)
14.某公司欲招聘职员,对应聘者进行三项测试:语言、创新、综合知识,并按测试得分1:3:2的比例确定测试总分,已知某位应聘者三项得分(单位:分)分别为86,72,50,则这位应聘者的测试总分为 .
15.近日,生态环境部公布第六批“绿水青山就是金山银山”实践创新基地名单,山西省6个县入选国家生态文明建设示范区,为了响应对环境保护的号召,某校要从报名的甲、乙、丙三人中选取一人去参加太原市举办的环保演讲比赛,经过两轮初赛后,甲、乙、丙三人的平均成绩都是90,方差分别是,,.你认为 参加决赛比较合适.
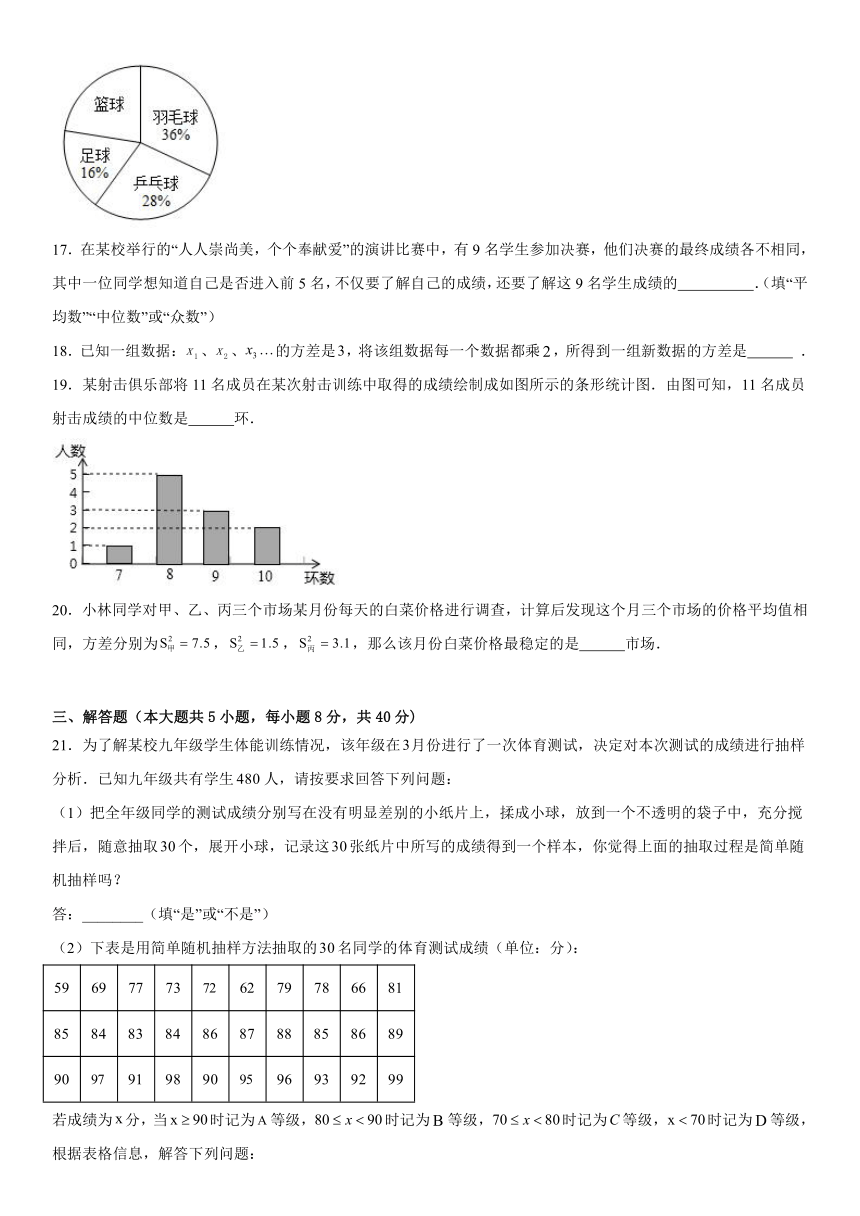
16.某校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目.为了了解全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中一个项目),并把调查结果绘制成如图所示的统计图,根据这个统计图可以估计该学校1500名学生中选择篮球项目的学生约为 名.
17.在某校举行的“人人崇尚美,个个奉献爱”的演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同,其中一位同学想知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的 .(填“平均数”“中位数”或“众数”)
18.已知一组数据:、、的方差是,将该组数据每一个数据都乘,所得到一组新数据的方差是 .
19.某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知,11名成员射击成绩的中位数是 环.
20.小林同学对甲、乙、丙三个市场某月份每天的白菜价格进行调查,计算后发现这个月三个市场的价格平均值相同,方差分别为,,,那么该月份白菜价格最稳定的是 市场.
三、解答题(本大题共5小题,每小题8分,共40分)
21.为了解某校九年级学生体能训练情况,该年级在月份进行了一次体育测试,决定对本次测试的成绩进行抽样分析.已知九年级共有学生人,请按要求回答下列问题:
(1)把全年级同学的测试成绩分别写在没有明显差别的小纸片上,揉成小球,放到一个不透明的袋子中,充分搅拌后,随意抽取个,展开小球,记录这张纸片中所写的成绩得到一个样本,你觉得上面的抽取过程是简单随机抽样吗?
答:________(填“是”或“不是”)
(2)下表是用简单随机抽样方法抽取的名同学的体育测试成绩(单位:分):
若成绩为分,当时记为等级,时记为等级,时记为等级,时记为等级,根据表格信息,解答下列问题:
①本次抽样调查获取的样本数据的中位数是________;估计全年级本次体育测试成绩在、两个等级的人数是________;
②经过一个多月的强化训练发现等级的同学平均成绩提高分,等级的同学平均成绩提高分,等级的同学平均成绩提高分,等级的同学平均成绩没有变化,请估计强化训练后全年级学生的平均成绩提高多少分?
22.某中学为了宣传防疫知识,在该校七、八两个年级开展了“防疫知识”大赛活动.为了了解参赛学生的成绩,从两个年级中各随机选取了名学生的成绩,数据如下:
七年级:92,97,88,92,94,95,92,95,97,98;
八年级:93,94,88,91,92,93,100,98,98,93.
通过整理,得到如下所示的数据分析表.
项目 平均分 中位数 众数 方差
七年级
八年级
(1)填空:_______,_______;
(2)通过计算说明哪个年级的成绩更稳定;
(3)学校规定,成绩不低于分的选手可以获奖,若该校七年级有人参加比赛,请估计七年级有多少人获奖.
23.某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图,请根据图中提供的信息解答下列问题:
(1)本次共调查了多少名学生;
(2)通过计算补全频数分布直方图;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
24.6月的第三个星期天是父亲节,某校组织了以“父爱如山”为主题的演讲比赛,根据初赛成绩,七、八年级各选出名学生组成代表队,参加决赛.并根据他们的决赛成绩绘制了如下两幅统计图表:(满分为分)
补全下表中的数据;
组别 平均数(分) 中位数(分) 众数(分)
七年级
八年级
结合两队决赛成绩的平均数和中位数,评价两个队的决赛成绩;
哪个年级代表队的决赛成绩更稳定.
25.新年伊始,中国电影行业迎来了开门红.春节档期全国总观影人次超过亿,总票房超过亿元.以下是甲、乙两部春节档影片上映后的票房信息.
a.两部影片上映第一周单日票房统计图
b.两部影片分时段累计票房如下
上映影片 2月12日—18日累计票房(亿元) 2月19日—21日累计票房(亿元)
甲
乙
根据以上信息,回答下列问题:
(1)2月12日—18日的一周时间内,影片甲单日票房的中位数为 ;
(2)对于甲、乙两部影片上映第一周的单日票房,下列说法中所有正确结论的序号是 ;
①甲的单日票房逐日增加;
②甲单日票房的方差小于乙单日票房的方差;
③在第一周的单日票房统计中,甲超过乙的差值于2月17日达到最大.
(3)截止到2月21日,影片甲上映后的总票房超过了影片乙,据此估计,2月19日—21日三天内影片甲的累计票房应超过 亿元.
参考答案:
1.A
2.D
3.B
4.B
5.B
6.A
7.A
8.C
9.D
10.A
11.C
12.C
13.>
14.67分
15.甲
16.300
17.中位数
18.
19.8
20.乙
21.(1)是;(2)①,;②
22.(1)94;93;(2)七年级学生的成绩更稳定;(3)七年级约有人获奖.
23.(1)100
(2)11
(3)870名
24.(1)85,80,85;(2)见解析;(3)七年级代表队学生成绩较为稳定
25.(1)4.36
(2)②③
(3)8.61
2023-2024学年九年级上册数学冀教版
一、单选题(本大题共12小题,每小题3分,共36分)
1.近几年受新冠肺炎病毒影响,多地学校开展停课不停学网上教学活动,梁老师调查统计了本班40名学生一天利用网课学习的时间(单位:小时)如表:
时间(小时) 3小时或以下 4 5 6 7 8小时或以上
人数(个) 4 6 20 5 3 2
这组数据的众数是( )
A.5 B.6 C.8 D.20
2.清溪中学在劳动基地开展主题为“春种秋收”的劳动教育活动,九年级(1)班师生共参与了剪枝、锄地、除草、浇水、施肥五项实践活动,已知五个项目的参与人数分别是,则这组数据的众数和中位数分别是( )
A.11,9 B.10,9 C.10,11 D.11,11
3.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A.160 B.165 C.170 D.175
4.一个射手连续射靶10次,其中3次射中10环,3次射中9环,4次射中8环.则该射手射中环数的中位数和众数分别为( )
A.8,9 B.9,8 C.8.5,8 D.8.5,9
5.五个绿化小组一天植树的棵树如下:10、10、12、、8.已知这组数据的众数与平均数相同,那么这组数据的平均数是( )
A.12 B.10 C.8 D.9
6.在庆祝中国共产党成立100周年的校园歌唱比赛中,15名参赛同学的成绩各不相同,按照成绩取前7名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这15名同学成绩的( )
A.中位数 B.众数 C.平均数 D.方差
7.为了推选一名同学参加学校举办的“中国汉字听写大赛”,九(3)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.8,根据以上数据,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
8.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数x与方差s2如下表所示:
甲 乙 丙 丁
平均数 8.0 8.0 8.5 8.5
方差s2 3.5 15.5 3.5 16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
9.A、B、C、D、E五名射击运动员在一次比赛中的平均成绩是80环,而A、B、C三人的平均成绩是78环,那么下列说法中一定正确的是( )
A.D、E的成绩比其他三人好
B.B、E两人的平均成绩是83环
C.最高分得主不是A、B、C
D.D、E中至少有1人的成绩不少于83环.
10.为庆祝2023年5月30日神舟十六号成功发射,学校开展航天知识竞赛活动,经过几轮筛选,某班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经统计,四名同学成绩的平均数(单位:分)及方差(单位:分)如下表:
甲 乙 丙 丁
平均数 97 95 97 93
方差 0.3 1.2 1.3 0.6
根据表中数据,要选一名成绩好且状态稳定的同学参赛,应选择( )
A.甲 B.乙 C.丙 D.丁
11.下表记录了甲、乙、丙、丁四名同学最近五次数学考试成绩的平均分与方差∶
甲 乙 丙 丁
平均分 93 96 96 93
方差 5.1 5.1 1.2 1.2
要选择一名成绩好且发挥稳定的同学参加数学比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
12.下列说法正确的是( )
A.在小明,小红,小月三人中抽2人参加比赛,小刚被轴中是随机事件
B.要了解学校2000学生的体质健康情况,随机抽取100名学生进行调查,在该调查中样本容量是100名学生
C.预防“新冠病毒”期间,有关部门对某商店在售口罩的合格情况进行抽检,抽检了20包口罩,其中18包合格,该商店共进货100包,估计合格的口罩约有90包
D.了解某班学生的身高情况适宜抽样调查
二、填空题(本大题共8小题,每小题3分,共24分)
13.小华、小明两位射击运动员在选拔赛中各射击10次的成绩如图所示,他们的平均成绩均为7.5环,若小华射击10次成绩的方差为,小明射击10次成绩的方差为,则 .(填“>,<,=”)
14.某公司欲招聘职员,对应聘者进行三项测试:语言、创新、综合知识,并按测试得分1:3:2的比例确定测试总分,已知某位应聘者三项得分(单位:分)分别为86,72,50,则这位应聘者的测试总分为 .
15.近日,生态环境部公布第六批“绿水青山就是金山银山”实践创新基地名单,山西省6个县入选国家生态文明建设示范区,为了响应对环境保护的号召,某校要从报名的甲、乙、丙三人中选取一人去参加太原市举办的环保演讲比赛,经过两轮初赛后,甲、乙、丙三人的平均成绩都是90,方差分别是,,.你认为 参加决赛比较合适.
16.某校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目.为了了解全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中一个项目),并把调查结果绘制成如图所示的统计图,根据这个统计图可以估计该学校1500名学生中选择篮球项目的学生约为 名.
17.在某校举行的“人人崇尚美,个个奉献爱”的演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同,其中一位同学想知道自己是否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的 .(填“平均数”“中位数”或“众数”)
18.已知一组数据:、、的方差是,将该组数据每一个数据都乘,所得到一组新数据的方差是 .
19.某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知,11名成员射击成绩的中位数是 环.
20.小林同学对甲、乙、丙三个市场某月份每天的白菜价格进行调查,计算后发现这个月三个市场的价格平均值相同,方差分别为,,,那么该月份白菜价格最稳定的是 市场.
三、解答题(本大题共5小题,每小题8分,共40分)
21.为了解某校九年级学生体能训练情况,该年级在月份进行了一次体育测试,决定对本次测试的成绩进行抽样分析.已知九年级共有学生人,请按要求回答下列问题:
(1)把全年级同学的测试成绩分别写在没有明显差别的小纸片上,揉成小球,放到一个不透明的袋子中,充分搅拌后,随意抽取个,展开小球,记录这张纸片中所写的成绩得到一个样本,你觉得上面的抽取过程是简单随机抽样吗?
答:________(填“是”或“不是”)
(2)下表是用简单随机抽样方法抽取的名同学的体育测试成绩(单位:分):
若成绩为分,当时记为等级,时记为等级,时记为等级,时记为等级,根据表格信息,解答下列问题:
①本次抽样调查获取的样本数据的中位数是________;估计全年级本次体育测试成绩在、两个等级的人数是________;
②经过一个多月的强化训练发现等级的同学平均成绩提高分,等级的同学平均成绩提高分,等级的同学平均成绩提高分,等级的同学平均成绩没有变化,请估计强化训练后全年级学生的平均成绩提高多少分?
22.某中学为了宣传防疫知识,在该校七、八两个年级开展了“防疫知识”大赛活动.为了了解参赛学生的成绩,从两个年级中各随机选取了名学生的成绩,数据如下:
七年级:92,97,88,92,94,95,92,95,97,98;
八年级:93,94,88,91,92,93,100,98,98,93.
通过整理,得到如下所示的数据分析表.
项目 平均分 中位数 众数 方差
七年级
八年级
(1)填空:_______,_______;
(2)通过计算说明哪个年级的成绩更稳定;
(3)学校规定,成绩不低于分的选手可以获奖,若该校七年级有人参加比赛,请估计七年级有多少人获奖.
23.某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图,请根据图中提供的信息解答下列问题:
(1)本次共调查了多少名学生;
(2)通过计算补全频数分布直方图;
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数.
24.6月的第三个星期天是父亲节,某校组织了以“父爱如山”为主题的演讲比赛,根据初赛成绩,七、八年级各选出名学生组成代表队,参加决赛.并根据他们的决赛成绩绘制了如下两幅统计图表:(满分为分)
补全下表中的数据;
组别 平均数(分) 中位数(分) 众数(分)
七年级
八年级
结合两队决赛成绩的平均数和中位数,评价两个队的决赛成绩;
哪个年级代表队的决赛成绩更稳定.
25.新年伊始,中国电影行业迎来了开门红.春节档期全国总观影人次超过亿,总票房超过亿元.以下是甲、乙两部春节档影片上映后的票房信息.
a.两部影片上映第一周单日票房统计图
b.两部影片分时段累计票房如下
上映影片 2月12日—18日累计票房(亿元) 2月19日—21日累计票房(亿元)
甲
乙
根据以上信息,回答下列问题:
(1)2月12日—18日的一周时间内,影片甲单日票房的中位数为 ;
(2)对于甲、乙两部影片上映第一周的单日票房,下列说法中所有正确结论的序号是 ;
①甲的单日票房逐日增加;
②甲单日票房的方差小于乙单日票房的方差;
③在第一周的单日票房统计中,甲超过乙的差值于2月17日达到最大.
(3)截止到2月21日,影片甲上映后的总票房超过了影片乙,据此估计,2月19日—21日三天内影片甲的累计票房应超过 亿元.
参考答案:
1.A
2.D
3.B
4.B
5.B
6.A
7.A
8.C
9.D
10.A
11.C
12.C
13.>
14.67分
15.甲
16.300
17.中位数
18.
19.8
20.乙
21.(1)是;(2)①,;②
22.(1)94;93;(2)七年级学生的成绩更稳定;(3)七年级约有人获奖.
23.(1)100
(2)11
(3)870名
24.(1)85,80,85;(2)见解析;(3)七年级代表队学生成绩较为稳定
25.(1)4.36
(2)②③
(3)8.61
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
