鲁教版(五四学制) 六年级下册 5.2线段的长短与比较 课件 (共35张PPT)
文档属性
| 名称 | 鲁教版(五四学制) 六年级下册 5.2线段的长短与比较 课件 (共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 656.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 11:27:30 | ||
图片预览









文档简介
(共35张PPT)
线段的长短与比较
Honeybee
目录
Honeybee
回顾与思考
02
线段的比较
03
线段的做法
04
线段的中点
05
学习目标
01
课堂总结
06
01
PART ONE
学习目标
学习目标
1、掌握“两点之间线段最短”的基本性质,理解两点间距离的意义,能度量两点之间的距离。(重点)
2、会比较两条线段的大小,并会用符号“>”“<”“=”表示。
3、会用直尺和圆规作一条线段,使它等于已知线段。(重难点)
4、理解线段的和、差以及线段中点的意义,能用直尺和圆规作出线段的和、差,会用刻度尺画出一条线段的中点,并能用符号语言表示出来(难点)感受符号语言在描述图形中的重要作用。
5、培养自己的观察和动手能力。
02
PART ONE
回顾与思考
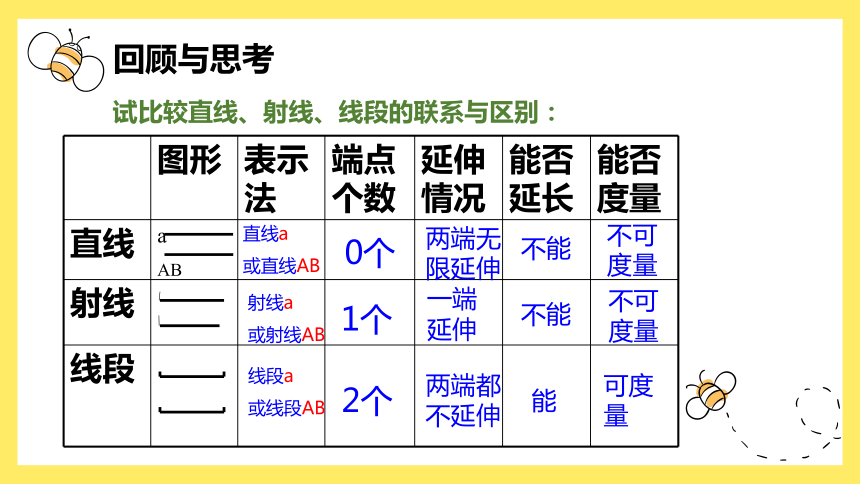
回顾与思考
图形 表示法 端点个数 延伸情况 能否延长 能否度量
直线
射线
线段
试比较直线、射线、线段的联系与区别:
射线a
或射线AB
直线a
或直线AB
线段a
或线段AB
0个
1个
2个
两端无
限延伸
一端
延伸
两端都
不延伸
不可度量
不可度量
可度量
a
AB
不能
不能
能
03
PART ONE
线段的比较
线段的基本事实
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
怎样走最近呢?
两点的所有连线中,线段最短.
(即两点之间,线段最短)
连接两点间的线段的长度,叫做这两点的距离。
探索
“两点之间的线段”和“两点间的距离”有何区别
两点之间的线段是图形.
两点之间线段的长度才是两点的距离,它是一个数量, 且有长度单位.
因此不能说线段是距离.
在学校400米环形跑道进行田径赛,田径赛中的200米跑,是指跑道的起点到终点的距离是200米吗?
不对.因为200米不是起点到终点的线段的长,而是曲线跑道的长.
例题讲练
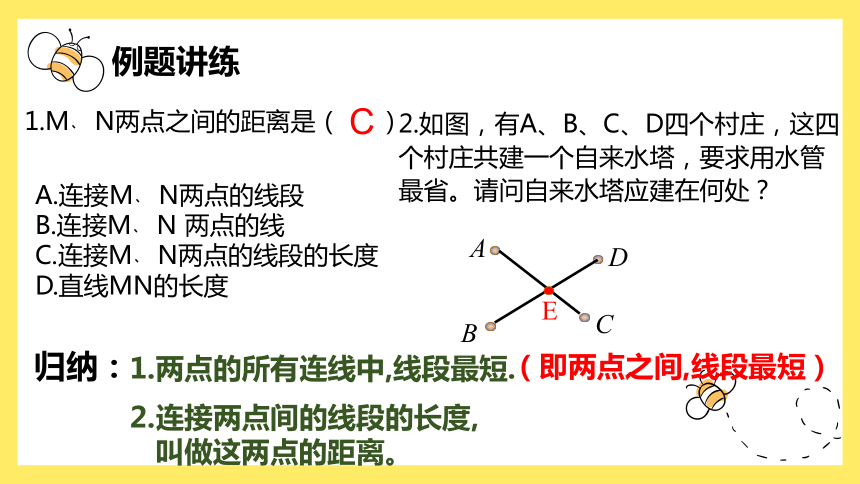
1.M﹑N两点之间的距离是( )
A.连接M﹑N两点的线段
B.连接M﹑N 两点的线
C.连接M﹑N两点的线段的长度
D.直线MN的长度
C
1.两点的所有连线中,线段最短.
(即两点之间,线段最短)
2.连接两点间的线段的长度,
叫做这两点的距离。
归纳:
A
B
C
D
2.如图,有A、B、C、D四个村庄,这四个村庄共建一个自来水塔,要求用水管最省。请问自来水塔应建在何处?
E
思考
思考 :怎样比较两个同学的高矮
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
① 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
知识应用
C
D
A
B
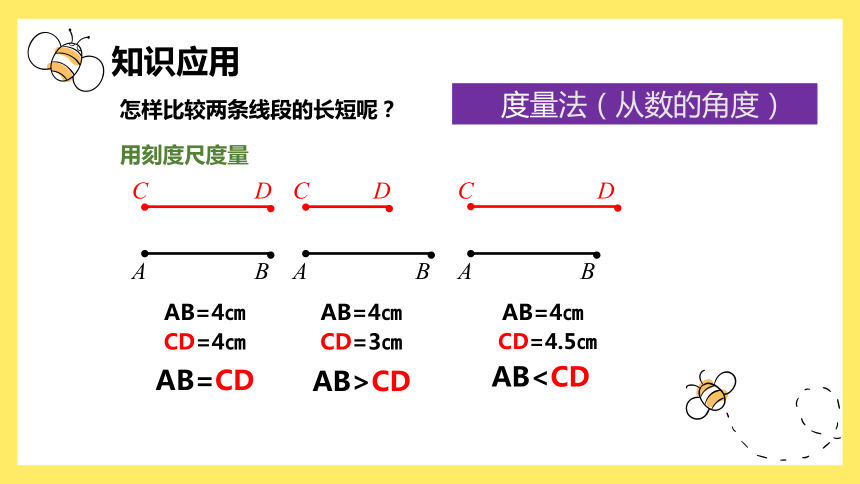
AB=4㎝
CD=4㎝
AB=CD
C
D
A
B
AB=4㎝
CD=3㎝
AB>CD
C
D
A
B
AB=4㎝
CD=4.5㎝
AB怎样比较两条线段的长短呢?
度量法(从数的角度)
用刻度尺度量
知识应用
怎样比较两条线段的长短呢?
将AB,CD放在同一条直线上,使端点A与C重合,端点B与D落在A的同一侧。
C
D
A
B
C
D
A
B
C
D
A
B
点D与B重合
AB=CD
点D在线段AB 内部
AB>CD
点D在线段AB延长线上
AB叠合法(从形的角度)
归纳
线段大小比较 度量法 叠合法
比较步骤
①用刻度尺测量长度;
②根据长度比较大小,长度大的线段大
①对端点;(使一个端点重合)
③看另一端点作判断。
②叠合:(在同一直线上,端点同侧)
线段的和与差
在右图中,点C在线段AB的延长线上,
B
A
C
a
b
图中三条线段AB,BC,AC有怎样的关系?
那么线段AC就是a与b的和,记作AC=a+b.
如果线段AB=a,线段BC=b,
线段的和
线段的和与差
在右图中,点D在线段AB上,
如果线段AB=a,线段DB=b,
那么线段AD就是a与b的差,记作AD=a-b
B
A
D
a
b
图中三条线段AB,BD,AD又有怎样的关系?
线段的差
例题讲练
C
B
A
1、 (1)CB = + ;
(2)AC = - ;
(3)AB = - ;
C
B
A
b
a
2、如右图,若AB=a , AC=b
则CB = + ;
C
B
A
b
a
3、如右图,若AB=a , BC=b
则AC = - ;
a
a
b
b
AC
BC
AB
BC
AB
AC
04
PART ONE
尺规作图
线段的做法
注意:在不要求写画法时,一定要标清字母,写出结论.
(1) 用直尺画射线AC ;
A C
B
所以 AB=a.
作 法:
已知线段a,画线段AB,使AB=a.
画一条线段等于已知线段
(2)用圆规 在射线AC上截取AB=a.
a
拓展提升
A
①先画一条直线 l ;
②在直线 l 上依次截取
AC = a ,CB=b。
已知线段a、b,画一条线段AB,
使AB=a+b.
b
C
a
b
B
所以AB=a+b.
作 法:
l
a
拓展提升
A
l
①先用直尺画一条直线 l ;
②在直线 l 上截取AD = b;
已知线段a,b(b>a)画一条线段AC,
使AC=b-a。
a
b
C
b
D
所以AC=b-a。
作 法:
a
在线段AD上截取DC=a。
归纳
线段的画法
截取法
度量法
注意:不要求大家写画法时,一定要保留作图痕迹,标清字母,写出结论.
要一量,
二算,
三画.
05
PART ONE
线段的中点
思考
你能用这根绳子正好做一双鞋带吗?
A
B
C
拿出一张纸,对折这张纸,把纸展开铺平,发现在边AB上有一个折痕点C,问AC和BC相等吗?
线段的中点
A
B
M
点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.
如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.
文字叙述:
数学符号语言:
因为点M是线段AB的中点
所以AM=MB= AB,AB=2AM=2BM
知识应用
1、如图①,AD=AB- =AC+ 。
图①
图②
2、如图②,下列说法不能判断点C是线段
的中点的是( )
( A)AC=CB ( B)AB=2AC
(C)AC+CB=AB ( D)2CB=AB
DB
CD
C
C
B
A
拓展提升
A
B
M
N
A
B
M
M、N为线段AB的三等分点
AM=MN=NB= AB; AB=3AM=3MN=3NB
N
P
M、N、P为线段AB的四等分点
AN=MN=MP=PB= AB;
AB=4AN=4MN=4NP=4PB
例题讲练
例1、如图①,AD=AB- =AC+ 。
图①
图②
例2、如图②,下列说法不能判断点C是线段
的中点的是( )
( A)AC=CB ( B)AB=2AC
(C)AC+CB=AB ( D)2CB=AB
DB
CD
C
C
B
A
例题讲练
例3、 AB=6cm,点C是线段AB的中点,点D是
线段CB的中点,求线段AD的长。
B
C
A
D
解:
因为AB=6,C是线段AB的中点
所以AC=BC= AB=3cm
因为D是线段CB的中点
所以CD= CB= 1.5cm
所以AD=AC+CD=4.5cm
故线段AD的长等于4.5cm.
符号语言
因为......,所以......
例题讲练
例4、 在直线上顺次取出A、B、C三点使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:因为AB=4cm BC=3cm,
所以AC=AB+BC=7cm,
因为点O是线段AC的中点,
所以OC= AC =3.5cm,
所以OB=OC-BC =3.5-3 =0.5(cm)。
答:线段OB的长为0.5cm。
例题讲练
例5、如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度。
。
。
。
。
A
C
D
B
∵ 点D是线段CB的中点,
∵ AD=8厘米,AB=10厘米,
∴ BD=AB-AD =2厘米
∴ CD =BD
∴ CB=2BD=4厘米
解:
06
PART ONE
课堂总结
课堂总结
1.线段的基本性质:
两点之间线段最短。
2.两点之间的距离:
两点之间线段的长度。
3.线段的两种比较方法:
叠合法和测量法。
5.用尺规法如何作图。
6.线段中点的概念及表示方法,中点的确定,线段的有关计算
4.线段和与差的计算
感谢聆听
Honeybee
课后作业
自我检测
1、已知:线段AB=4,延长AB至点C,使AC=11。点D是AB的中点,点E是AC的中点。求DE的长。
2、已知线段AB=12cm,点M是它的一个三等分点,则AM=___________cm.
3.课本作图题
线段的长短与比较
Honeybee
目录
Honeybee
回顾与思考
02
线段的比较
03
线段的做法
04
线段的中点
05
学习目标
01
课堂总结
06
01
PART ONE
学习目标
学习目标
1、掌握“两点之间线段最短”的基本性质,理解两点间距离的意义,能度量两点之间的距离。(重点)
2、会比较两条线段的大小,并会用符号“>”“<”“=”表示。
3、会用直尺和圆规作一条线段,使它等于已知线段。(重难点)
4、理解线段的和、差以及线段中点的意义,能用直尺和圆规作出线段的和、差,会用刻度尺画出一条线段的中点,并能用符号语言表示出来(难点)感受符号语言在描述图形中的重要作用。
5、培养自己的观察和动手能力。
02
PART ONE
回顾与思考
回顾与思考
图形 表示法 端点个数 延伸情况 能否延长 能否度量
直线
射线
线段
试比较直线、射线、线段的联系与区别:
射线a
或射线AB
直线a
或直线AB
线段a
或线段AB
0个
1个
2个
两端无
限延伸
一端
延伸
两端都
不延伸
不可度量
不可度量
可度量
a
AB
不能
不能
能
03
PART ONE
线段的比较
线段的基本事实
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线.
A
B
怎样走最近呢?
两点的所有连线中,线段最短.
(即两点之间,线段最短)
连接两点间的线段的长度,叫做这两点的距离。
探索
“两点之间的线段”和“两点间的距离”有何区别
两点之间的线段是图形.
两点之间线段的长度才是两点的距离,它是一个数量, 且有长度单位.
因此不能说线段是距离.
在学校400米环形跑道进行田径赛,田径赛中的200米跑,是指跑道的起点到终点的距离是200米吗?
不对.因为200米不是起点到终点的线段的长,而是曲线跑道的长.
例题讲练
1.M﹑N两点之间的距离是( )
A.连接M﹑N两点的线段
B.连接M﹑N 两点的线
C.连接M﹑N两点的线段的长度
D.直线MN的长度
C
1.两点的所有连线中,线段最短.
(即两点之间,线段最短)
2.连接两点间的线段的长度,
叫做这两点的距离。
归纳:
A
B
C
D
2.如图,有A、B、C、D四个村庄,这四个村庄共建一个自来水塔,要求用水管最省。请问自来水塔应建在何处?
E
思考
思考 :怎样比较两个同学的高矮
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
① 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较。
——度量法.
知识应用
C
D
A
B
AB=4㎝
CD=4㎝
AB=CD
C
D
A
B
AB=4㎝
CD=3㎝
AB>CD
C
D
A
B
AB=4㎝
CD=4.5㎝
AB
度量法(从数的角度)
用刻度尺度量
知识应用
怎样比较两条线段的长短呢?
将AB,CD放在同一条直线上,使端点A与C重合,端点B与D落在A的同一侧。
C
D
A
B
C
D
A
B
C
D
A
B
点D与B重合
AB=CD
点D在线段AB 内部
AB>CD
点D在线段AB延长线上
AB
归纳
线段大小比较 度量法 叠合法
比较步骤
①用刻度尺测量长度;
②根据长度比较大小,长度大的线段大
①对端点;(使一个端点重合)
③看另一端点作判断。
②叠合:(在同一直线上,端点同侧)
线段的和与差
在右图中,点C在线段AB的延长线上,
B
A
C
a
b
图中三条线段AB,BC,AC有怎样的关系?
那么线段AC就是a与b的和,记作AC=a+b.
如果线段AB=a,线段BC=b,
线段的和
线段的和与差
在右图中,点D在线段AB上,
如果线段AB=a,线段DB=b,
那么线段AD就是a与b的差,记作AD=a-b
B
A
D
a
b
图中三条线段AB,BD,AD又有怎样的关系?
线段的差
例题讲练
C
B
A
1、 (1)CB = + ;
(2)AC = - ;
(3)AB = - ;
C
B
A
b
a
2、如右图,若AB=a , AC=b
则CB = + ;
C
B
A
b
a
3、如右图,若AB=a , BC=b
则AC = - ;
a
a
b
b
AC
BC
AB
BC
AB
AC
04
PART ONE
尺规作图
线段的做法
注意:在不要求写画法时,一定要标清字母,写出结论.
(1) 用直尺画射线AC ;
A C
B
所以 AB=a.
作 法:
已知线段a,画线段AB,使AB=a.
画一条线段等于已知线段
(2)用圆规 在射线AC上截取AB=a.
a
拓展提升
A
①先画一条直线 l ;
②在直线 l 上依次截取
AC = a ,CB=b。
已知线段a、b,画一条线段AB,
使AB=a+b.
b
C
a
b
B
所以AB=a+b.
作 法:
l
a
拓展提升
A
l
①先用直尺画一条直线 l ;
②在直线 l 上截取AD = b;
已知线段a,b(b>a)画一条线段AC,
使AC=b-a。
a
b
C
b
D
所以AC=b-a。
作 法:
a
在线段AD上截取DC=a。
归纳
线段的画法
截取法
度量法
注意:不要求大家写画法时,一定要保留作图痕迹,标清字母,写出结论.
要一量,
二算,
三画.
05
PART ONE
线段的中点
思考
你能用这根绳子正好做一双鞋带吗?
A
B
C
拿出一张纸,对折这张纸,把纸展开铺平,发现在边AB上有一个折痕点C,问AC和BC相等吗?
线段的中点
A
B
M
点M把线段AB分成相等的两条线段AM与MB,我们把M点叫做线段AB的中点.
如果我们把拉直的线绳看作线段AB,刚才的折点看作点M,观察线段AM与BM的关系.
文字叙述:
数学符号语言:
因为点M是线段AB的中点
所以AM=MB= AB,AB=2AM=2BM
知识应用
1、如图①,AD=AB- =AC+ 。
图①
图②
2、如图②,下列说法不能判断点C是线段
的中点的是( )
( A)AC=CB ( B)AB=2AC
(C)AC+CB=AB ( D)2CB=AB
DB
CD
C
C
B
A
拓展提升
A
B
M
N
A
B
M
M、N为线段AB的三等分点
AM=MN=NB= AB; AB=3AM=3MN=3NB
N
P
M、N、P为线段AB的四等分点
AN=MN=MP=PB= AB;
AB=4AN=4MN=4NP=4PB
例题讲练
例1、如图①,AD=AB- =AC+ 。
图①
图②
例2、如图②,下列说法不能判断点C是线段
的中点的是( )
( A)AC=CB ( B)AB=2AC
(C)AC+CB=AB ( D)2CB=AB
DB
CD
C
C
B
A
例题讲练
例3、 AB=6cm,点C是线段AB的中点,点D是
线段CB的中点,求线段AD的长。
B
C
A
D
解:
因为AB=6,C是线段AB的中点
所以AC=BC= AB=3cm
因为D是线段CB的中点
所以CD= CB= 1.5cm
所以AD=AC+CD=4.5cm
故线段AD的长等于4.5cm.
符号语言
因为......,所以......
例题讲练
例4、 在直线上顺次取出A、B、C三点使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:因为AB=4cm BC=3cm,
所以AC=AB+BC=7cm,
因为点O是线段AC的中点,
所以OC= AC =3.5cm,
所以OB=OC-BC =3.5-3 =0.5(cm)。
答:线段OB的长为0.5cm。
例题讲练
例5、如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度。
。
。
。
。
A
C
D
B
∵ 点D是线段CB的中点,
∵ AD=8厘米,AB=10厘米,
∴ BD=AB-AD =2厘米
∴ CD =BD
∴ CB=2BD=4厘米
解:
06
PART ONE
课堂总结
课堂总结
1.线段的基本性质:
两点之间线段最短。
2.两点之间的距离:
两点之间线段的长度。
3.线段的两种比较方法:
叠合法和测量法。
5.用尺规法如何作图。
6.线段中点的概念及表示方法,中点的确定,线段的有关计算
4.线段和与差的计算
感谢聆听
Honeybee
课后作业
自我检测
1、已知:线段AB=4,延长AB至点C,使AC=11。点D是AB的中点,点E是AC的中点。求DE的长。
2、已知线段AB=12cm,点M是它的一个三等分点,则AM=___________cm.
3.课本作图题
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
