2.3确定二次函数的表达式基础练习(含简单答案)北师大版数学九年级下册
文档属性
| 名称 | 2.3确定二次函数的表达式基础练习(含简单答案)北师大版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 12:00:05 | ||
图片预览



文档简介
2.3确定二次函数的表达式基础练习-北师大版数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知二次函数的对称轴为,点在此函数的像上,则有( )
A. B. C. D.
2.某同学在利用描点法画二次函数的图象时,先取自变量x的一些值计算出相应的函数值y,如下表所示:
x … 0 1 2 3 4 …
y … -3 0 -1 0 -3 …
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. B. C. D.
3.下表中所列的,的6对值是二次函数的图象上的点所对应的坐标:
0 3 4
11 6 3 6 11
若,是该函数图象上的两点,根据表中信息,以下论断正确的是( )
A.当时, B.当时,
C.该函数的最小值为3 D.当,时(为常数),
4.如图,是二次函数的图象,对下列结论①ab>0,②abc>0,③,其中错误的个数是( )
A.3 B.2 C.1 D.0
5.如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
A.b2>4ac B.m>n C.方程ax2+bx+c=﹣4的两根为﹣5或﹣1 D.ax2+bx+c≥﹣6
6.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:
x 0 1 2 3 4
y 3 0 -2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式( )
A.y= B.y=x2-4x+3 C. D.
7.已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中,自变量x与函数值y之间满足下面对应关系:
x …… 5 3 1 ……
y=ax2+bx+c …… 2.5 1.5 1.5 ……
则的值是( )
A.﹣10 B.﹣5 C.﹣ D.﹣
8.已知抛物线的顶点坐标为,则抛物线对应的函数解析式为( )
A. B. C. D.
9.已知二次函数y=ax2+bx+1,若当x=1时,y=0;当x=﹣1时,y=4,则a、b的值分别为( )
A.a=1,b=2 B.a=1,b=﹣2 C.a=﹣1,b=2 D.a=﹣1,b=﹣2
10.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣1 0 ﹣3 ﹣4 ﹣3 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣1 B.﹣3 C.0 D.﹣4
二、填空题
11.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:
序号 ① ② ③ ④ ⑤
x 0 1 2 3 4
y 3 0 ﹣2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你找出错误的那组数据 .(只填序号)
12.将抛物线先向下平移3个单位,再向右平移个单位,所得新抛物线经过点.新抛物线的表达式为 .
13.二次函数y=x2-2x+m的图象与x轴的一个交点的坐标是(-1,0),则图像与x轴的另一个交点的坐标是 .
14.对于函数(a为常数),当时,,则当时, .
15.二次函数与y轴的交点到原点的距离为8,它的顶点坐标为,那么它的解析式为 .
16.二次函数表达式沿x轴翻折的表达式为 .
17.平移二次函数的图象,如果有一个点既在平移前的函数图象上,又在平移后的函数图象上,我们把这个点叫做“关联点”.现将二次函数(c为常数)的图象向右平移得到新的抛物线,若“关联点”为,则新抛物线的函数表达式为 .
18.已知二次函数y与自变量x的部分对应值如表:
… 0 1 3 4 8 …
… 7 0 0 40 …
则二次函数的解析式为 .
19.已知抛物线y=ax2+bx+c的图象与x轴交于点A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和C(2m﹣4,m﹣6),抛物线y=ax2+bx+c与y轴交于点D,点P在抛物线的对称轴上,连PA,PD,当PA+PD的长最短时,点P的坐标为 .
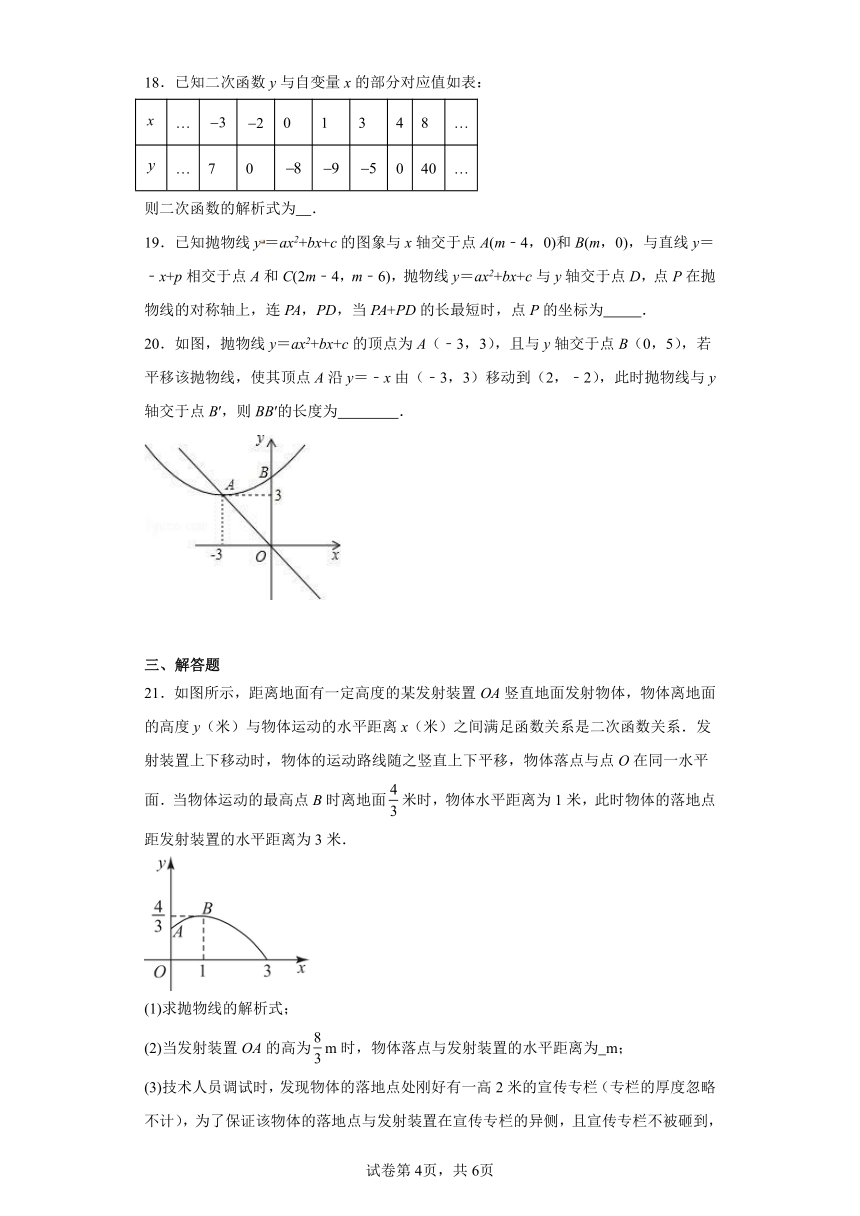
20.如图,抛物线y=ax2+bx+c的顶点为A(﹣3,3),且与y轴交于点B(0,5),若平移该抛物线,使其顶点A沿y=﹣x由(﹣3,3)移动到(2,﹣2),此时抛物线与y轴交于点B′,则BB′的长度为 .
三、解答题
21.如图所示,距离地面有一定高度的某发射装置OA竖直地面发射物体,物体离地面的高度y(米)与物体运动的水平距离x(米)之间满足函数关系是二次函数关系.发射装置上下移动时,物体的运动路线随之竖直上下平移,物体落点与点O在同一水平面.当物体运动的最高点B时离地面米时,物体水平距离为1米,此时物体的落地点距发射装置的水平距离为3米.
(1)求抛物线的解析式;
(2)当发射装置OA的高为m时,物体落点与发射装置的水平距离为 m;
(3)技术人员调试时,发现物体的落地点处刚好有一高2米的宣传专栏(专栏的厚度忽略不计),为了保证该物体的落地点与发射装置在宣传专栏的异侧,且宣传专栏不被砸到,技术人员则要调整发射装置的高度,问发射装置的高度至少为多少米时,该物体不被砸到?
22.已知抛物线关于y轴对称,且过点和点.
(1)求抛物线的解析式;
(2)若点和点在抛物线上,试比较p,q的大小;
(3)过点作与y轴不垂直的直线交抛物线于点A和点B,线段AB的垂直平分线交y轴于点M,试探究是否为定值?若是,求出定值;若不是,请说明理由.
23.如图1,在平面直角坐标系中,一次函数的图象分别交轴于点,抛物线经过点,点P为第四象限内抛物线上的一个动点.
(1)写出点A、点B的坐标;
(2)求此抛物线对应的函数表达式;
(3)如图2,过点P作PM//y轴,分别交直线轴于点,若以点为顶点的三角形与相似,求点P的坐标.
24.已知是关于的二次函数,下表给出了与的几对对应值,求二次函数的解析式.
…… 0 1 2 3 ……
…… 0 3 4 3 0 ……
25.如图,抛物线与轴分别交于两点(点在点左侧),与轴交于点,点为第二象限内的抛物线上一点,连接,,,,求抛物线的解析式.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.B
3.D
4.C
5.B
6.B
7.A
8.A
9.B
10.A
11.③.
12.
13.(3,0)
14.2
15.或
16.
17.
18.
19.(1,﹣2)
20.6
21.(1);
(2)4;
(3)发射装置的高度至少为3米时,该物体不被砸到.
22.(1)
(2)当0<m<2时,p>q;
当m=0或者m=2时,p=q;
当m<0或者m>2时,p<q
(3)是,定值为2
23.(1)A(4,0),B(0,﹣2)
(2)
(3)点P的坐标是或
24.
25.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知二次函数的对称轴为,点在此函数的像上,则有( )
A. B. C. D.
2.某同学在利用描点法画二次函数的图象时,先取自变量x的一些值计算出相应的函数值y,如下表所示:
x … 0 1 2 3 4 …
y … -3 0 -1 0 -3 …
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. B. C. D.
3.下表中所列的,的6对值是二次函数的图象上的点所对应的坐标:
0 3 4
11 6 3 6 11
若,是该函数图象上的两点,根据表中信息,以下论断正确的是( )
A.当时, B.当时,
C.该函数的最小值为3 D.当,时(为常数),
4.如图,是二次函数的图象,对下列结论①ab>0,②abc>0,③,其中错误的个数是( )
A.3 B.2 C.1 D.0
5.如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
A.b2>4ac B.m>n C.方程ax2+bx+c=﹣4的两根为﹣5或﹣1 D.ax2+bx+c≥﹣6
6.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:
x 0 1 2 3 4
y 3 0 -2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你根据上述信息写出该二次函数的解析式( )
A.y= B.y=x2-4x+3 C. D.
7.已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0),其中,自变量x与函数值y之间满足下面对应关系:
x …… 5 3 1 ……
y=ax2+bx+c …… 2.5 1.5 1.5 ……
则的值是( )
A.﹣10 B.﹣5 C.﹣ D.﹣
8.已知抛物线的顶点坐标为,则抛物线对应的函数解析式为( )
A. B. C. D.
9.已知二次函数y=ax2+bx+1,若当x=1时,y=0;当x=﹣1时,y=4,则a、b的值分别为( )
A.a=1,b=2 B.a=1,b=﹣2 C.a=﹣1,b=2 D.a=﹣1,b=﹣2
10.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … ﹣2 ﹣1 0 1 2 …
y … ﹣1 0 ﹣3 ﹣4 ﹣3 …
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.﹣1 B.﹣3 C.0 D.﹣4
二、填空题
11.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如下表:
序号 ① ② ③ ④ ⑤
x 0 1 2 3 4
y 3 0 ﹣2 0 3
经检查,发现表格中恰好有一组数据计算错误,请你找出错误的那组数据 .(只填序号)
12.将抛物线先向下平移3个单位,再向右平移个单位,所得新抛物线经过点.新抛物线的表达式为 .
13.二次函数y=x2-2x+m的图象与x轴的一个交点的坐标是(-1,0),则图像与x轴的另一个交点的坐标是 .
14.对于函数(a为常数),当时,,则当时, .
15.二次函数与y轴的交点到原点的距离为8,它的顶点坐标为,那么它的解析式为 .
16.二次函数表达式沿x轴翻折的表达式为 .
17.平移二次函数的图象,如果有一个点既在平移前的函数图象上,又在平移后的函数图象上,我们把这个点叫做“关联点”.现将二次函数(c为常数)的图象向右平移得到新的抛物线,若“关联点”为,则新抛物线的函数表达式为 .
18.已知二次函数y与自变量x的部分对应值如表:
… 0 1 3 4 8 …
… 7 0 0 40 …
则二次函数的解析式为 .
19.已知抛物线y=ax2+bx+c的图象与x轴交于点A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和C(2m﹣4,m﹣6),抛物线y=ax2+bx+c与y轴交于点D,点P在抛物线的对称轴上,连PA,PD,当PA+PD的长最短时,点P的坐标为 .
20.如图,抛物线y=ax2+bx+c的顶点为A(﹣3,3),且与y轴交于点B(0,5),若平移该抛物线,使其顶点A沿y=﹣x由(﹣3,3)移动到(2,﹣2),此时抛物线与y轴交于点B′,则BB′的长度为 .
三、解答题
21.如图所示,距离地面有一定高度的某发射装置OA竖直地面发射物体,物体离地面的高度y(米)与物体运动的水平距离x(米)之间满足函数关系是二次函数关系.发射装置上下移动时,物体的运动路线随之竖直上下平移,物体落点与点O在同一水平面.当物体运动的最高点B时离地面米时,物体水平距离为1米,此时物体的落地点距发射装置的水平距离为3米.
(1)求抛物线的解析式;
(2)当发射装置OA的高为m时,物体落点与发射装置的水平距离为 m;
(3)技术人员调试时,发现物体的落地点处刚好有一高2米的宣传专栏(专栏的厚度忽略不计),为了保证该物体的落地点与发射装置在宣传专栏的异侧,且宣传专栏不被砸到,技术人员则要调整发射装置的高度,问发射装置的高度至少为多少米时,该物体不被砸到?
22.已知抛物线关于y轴对称,且过点和点.
(1)求抛物线的解析式;
(2)若点和点在抛物线上,试比较p,q的大小;
(3)过点作与y轴不垂直的直线交抛物线于点A和点B,线段AB的垂直平分线交y轴于点M,试探究是否为定值?若是,求出定值;若不是,请说明理由.
23.如图1,在平面直角坐标系中,一次函数的图象分别交轴于点,抛物线经过点,点P为第四象限内抛物线上的一个动点.
(1)写出点A、点B的坐标;
(2)求此抛物线对应的函数表达式;
(3)如图2,过点P作PM//y轴,分别交直线轴于点,若以点为顶点的三角形与相似,求点P的坐标.
24.已知是关于的二次函数,下表给出了与的几对对应值,求二次函数的解析式.
…… 0 1 2 3 ……
…… 0 3 4 3 0 ……
25.如图,抛物线与轴分别交于两点(点在点左侧),与轴交于点,点为第二象限内的抛物线上一点,连接,,,,求抛物线的解析式.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
2.B
3.D
4.C
5.B
6.B
7.A
8.A
9.B
10.A
11.③.
12.
13.(3,0)
14.2
15.或
16.
17.
18.
19.(1,﹣2)
20.6
21.(1);
(2)4;
(3)发射装置的高度至少为3米时,该物体不被砸到.
22.(1)
(2)当0<m<2时,p>q;
当m=0或者m=2时,p=q;
当m<0或者m>2时,p<q
(3)是,定值为2
23.(1)A(4,0),B(0,﹣2)
(2)
(3)点P的坐标是或
24.
25.
答案第1页,共2页
答案第1页,共2页
