重点专题:梯形的面积(专项训练)数学五年级上册苏教版(含答案)
文档属性
| 名称 | 重点专题:梯形的面积(专项训练)数学五年级上册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 10:14:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
重点专题:梯形的面积(专项训练)数学五年级上册苏教版
一、选择题
1.两个完全一样的直角三角形重叠成如图形状,形成两个梯形(阴影部分),这两个梯形的面积大小关系是( )。
A.B大 B.A大 C.相等 D.无法确定
2.在下图中,平行线之间的三个图形的面积相比,正确的是( )。
A.平行四边形的面积最大 B.三角形的面积最大
C.梯形的面积最大 D.三个图形的面积都相等
3.用一条线段把一个平行四边形任意分割成两个梯形,这两个梯形中( )总是相等的。
A.高 B.上底、下底之和 C.周长 D.面积
4.一个等腰梯形的周长是48cm,面积是96cm2,高是8cm,则腰长是( )厘米。
A.6 B.8 C.12 D.24
5.一个直角梯形,下底长7cm。上底增加4cm,这个直角梯形就正好变成一个长方形,同时面积增加7cm2。这个直角梯形的面积是( )cm2。
A.14.5 B.17.5 C.20.5
6.梯形的上底扩大到原来的2倍,下底也扩大到原来的2倍,高不变,那么它的面积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍
C.扩大到原来的8倍 D.无法判断
二、填空题
7.一个梯形的上、下底之和是36分米,是高的4倍,这个梯形的面积是 ( )平方分米。
8.一个直角梯形的上底、下底和高分别是10dm、12dm和8dm,它的面积是( )dm2;在梯形内画一个最大的正方形,正方形的面积是( )dm2。
9.下图中,梯形上底长20厘米,高4厘米,阴影部分面积是( )平方厘米。
10.下面梯形的面积是( )dm2。
11.一个梯形的上底是3.2厘米,下底是6.8厘米,面积是40平方厘米,高是( )厘米。
12.一个果园是梯形。它的上底是120米,下底是40米,高是80米。这个果园的面积是( )平方米。
三、判断题
13.两个面积相等的梯形一定能拼成一个平行四边形。( )
14.梯形的面积是平行四边形面积的一半。( )
15.梯形的上底下底越长,面积越大。( )
16.可以把梯形转化成三角形推导出面积公式. ( )
17.一个梯形的高不变,如果上底增加2cm,下底减少2cm,面积不变。( )
四、图形计算
18.求阴影部分面积。(单位:m)
19.下图中阴影部分是一块草坪的平面图,求这块草坪的面积。
五、解答题
20.用100米长的篱笆一面靠墙围成一个花圃(如图)。这个花圃的面积是多少?
21.惠民广场有一个梯形花坛(如下图)。如果每平方米花坛种花16株,这个花坛一共可种花多少株?
22.下面每个小方格的边长都表示1厘米,请你按要求画图。
(1)画出一个面积是15平方厘米的平行四边形。
(2)画一个面积是12平方厘米、高是3厘米的梯形。
(3)用数对表示平行四边形各个顶点的位置。
23.一堆钢管,堆成梯形状,最下层102根,最上层38根,共堆有65层,这堆钢管共有多少根?
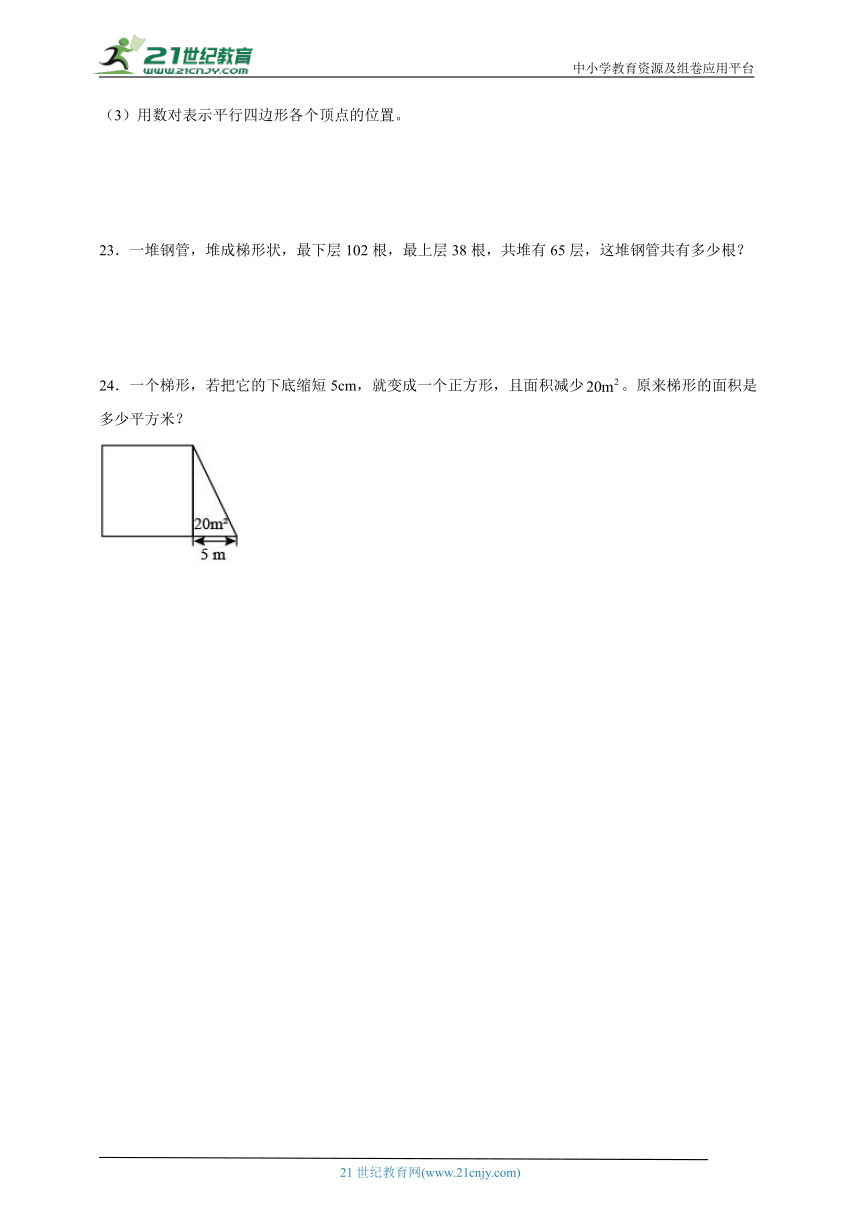
24.一个梯形,若把它的下底缩短5cm,就变成一个正方形,且面积减少。原来梯形的面积是多少平方米?
参考答案:
1.C
【分析】由题干可知,梯形A的面积=直角三角形面积-重叠部分面积,梯形B的面积=直角三角形面积-重叠部分面积,故梯形A的面积和梯形B的面积相等,据此解答。
【详解】由分析得,这两个梯形的面积的大小关系是:它们的面积相等。
故答案为:C
【点睛】此题考查的是平面图形面积的比较,解答此题应注意两个完全一样的直角三角形重叠一部分这一条件。
2.D
【分析】由图可知,平行四边形、三角形、梯形的高相等,利用“平行四边形的面积=底×高”“三角形的面积=底×高÷2”“梯形的面积=(上底+下底)×高÷2”求出三个图形的面积,最后比较大小,据此解答。
【详解】假设平行四边形、三角形、梯形的高为h。
平行四边形的面积:4h
三角形的面积:8h÷2=4h
梯形的面积:(2+6)h÷2
=8h÷2
=4h
因为4h=4h=4h,所以三个图形的面积相等。
故答案为:D
【点睛】掌握平行四边形、三角形、梯形的面积计算公式是解答题目的关键。
3.A
【分析】根据梯形高的定义知,梯形是只有一组对边平行的四边形,梯形的高是指上底和下底之间的距离,把平行四边形任意分割成两个梯形时,两平行线之间距离是相等的,据此解答。
【详解】根据以上分析,把一个平行四边形任意分割成两个梯形,其中的高一定相等。
故答案为:A
【点睛】此题是考查平行四边形的特征,掌握平行四边形是两组对边平行,它们之间的距离总是相等是解题关键。
4.C
【分析】根据“梯形的上底+下底=梯形的面积×2÷高”,据此求出上底与下底的和,用周长减去上底与下底的和,再除以2即可求出腰长多少厘米。
【详解】96×2÷8
=192÷8
=24(厘米);
(48-24)÷2
=24÷2
=12(厘米);
故答案为:C。
【点睛】熟练掌握梯形面积和周长的公式并能灵活利用是解答本题的关键。
5.B
【分析】,增加的是三角形,根据三角形的高=面积×2÷底,求出三角形的高,即梯形的高,根据梯形面积=(上底+下底)×高÷2,计算即可。
【详解】7×2÷4=3.5(厘米)
7-4=3(厘米)
(3+7)×3.5÷2
=10×3.5÷2
=17.5(平方厘米)
故答案为:B
【点睛】关键是确定梯形的上底和高,掌握梯形和三角形面积公式。
6.A
【分析】梯形的上下底同时扩大到原来的2倍,高不变,则梯形的面积也扩大到原来的2倍。
【详解】假设原来梯形的上底是2cm,下底是4cm,高是3cm,则现在梯形的上底是4cm,下底是8cm,高是3cm,
原来梯形的面积:(2+4)×3÷2=6×3÷2=9(平方厘米)
现在梯形的面积:(4+8)×3÷2=12×3÷2=18(平方厘米)
18÷9=2,则现在梯形的面积比原来梯形的面积扩大了2倍。
故答案为:A
【点睛】运用梯形的面积计算公式表示出原来的面积和现在的面积,并计算出扩大的倍数是解答本题的关键。
7.162
【分析】根据题意,梯形的上、下底之和是高的4倍,用上、下底之和除以4,即是梯形的高;然后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】高:36÷4=9(分米)
面积:
36×9÷2
=324÷2
=162(平方分米)
这个梯形的面积是162平方分米。
【点睛】先求出梯形的高,再根据梯形的面积公式求解。
8. 88 64
【分析】根据公式:梯形面积=(上底+下底)×高÷2,代入数据计算即可;在梯形内画一个最大的正方形,那么这个正方形的边长与短边高相等,再用公式:正方形的面积=边长×边长,计算出面积即可,据此解答。
【详解】(10+12)×8÷2
=22×8÷2
=176÷2
=88(dm2)
8×8=64(dm2)
一个直角梯形的上底、下底和高分别是10dm、12dm和8dm,它的面积是88dm2;在梯形内画一个最大的正方形,正方形的面积是64dm2。
【点睛】此题考查了梯形的面积计算以及正方形的面积计算,关键能够结合条件理解如何画最大的正方形。
9.80
【分析】从图中可以看出,阴影部分是两个平行四边形,它们的高都等于梯形的高,它们的底相加等于梯形的上底,所以阴影部分可以看作是一个底为20厘米,高为4的平行四边形;根据平行四边形的面积=底×高,代入数据计算即可。
【详解】20×4=80(平方厘米)
【点睛】把两个阴影部分看成一个平行四边形,找到这个平行四边形与梯形的关系,以及掌握平行四边形的面积公式是解题的关键。
10.
【分析】依据梯形的面积公式求解即可。
【详解】梯形面积=(上底+下底)×高÷2
【点睛】此题的解题关键是掌握梯形的面积公式,依据公式即可求出答案。
11.8
【分析】变换梯形面积计算公式:高=面积×2÷(上底+下底),依此公式计算即可。
【详解】40×2÷(3.2+6.8)
=80÷10
=8(厘米)
【点睛】本题关键在于对梯形面积计算公式的理解。
12.6400
【分析】根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(120+40)×80÷2
=160×40
=6400(平方米)
【点睛】关键是掌握梯形的面积公式。
13.×
【分析】两个完全一样的梯形才能拼成平行四边形,两个面积相等的梯形不一定完全相同,所以面积相等的梯形不一定能拼成一个平行四边形,据此判断。
【详解】由分析可知:
两个面积相等的梯形一定能拼成一个平行四边形。原题干说法错误。
故答案为:×
【点睛】本题考查梯形和平行四边形的特征,明确它们的特征是解题的关键。
14.×
【分析】根据梯形的面积公式和平行四边形面积公式可以进行推理。
【详解】梯形面积公式是(上底+下底)×高÷2;平行四边形面积公式是底×高;若不知道二者底和高的大小关系,是没办法比较其面积大小的。
故答案为:×
【点睛】两个完全一样的梯形可以拼成一个平行四边形,此时梯形的面积等于所拼成的平行四边形面积的一半。
15.×
【分析】梯形的面积=(上底+下底)×高÷2,梯形的面积和梯形的上底、下底和高都有关系,所以梯形的上底下底越长,面积越大的说法是不正确的。
【详解】据分析知,“梯形的上底下底越长,面积越大”的说法是不正确的。
故答案为:×
【点睛】掌握并灵活运用梯形的面积公式,这是解决此题的关键。
16.
【详解】略
17.√
【详解】略
18.120m2
【分析】如图作辅助线,阴影部分被分成了2个三角形和一个梯形,计算出三个图形的面积之和即可。
【详解】
(7+10)×10÷2+7×7÷2+7×(10-7)÷2
=17×10÷2+7×7÷2+7×3÷2
=85+24.5+10.5
=120(m2)
19.375平方米
【分析】观察图形可知,阴影部分的面积=长方形的面积-梯形的面积,据此代入数值进行计算即可。
【详解】20×30-(20+30)×9÷2
=600-450÷2
=600-225
=375(平方米)
20.1050平方米
【分析】根据题图可知,花圃的形状为梯形,梯形上底与下底的和加上高为100米,用100-30即可求出梯形上底与下底和,再根据“梯形的面积=(上底+下底)×高÷2”解答即可。
【详解】(100-30)×30÷2
=70×30÷2
=1050(平方米);
答:这个花圃的面积是1050平方米。
【点睛】明确梯形上底与下底和是解答本题的关键,再根据梯形的面积公式解答。
21.336株
【分析】根据梯形的面积公式,先计算出这个梯形的面积,再将其乘16,求出这个花坛一共可种花多少株。
【详解】(4+10)×3÷2×16
=14×3÷2×16
=336(株)
答:这个花坛一共可种花336株。
【点睛】本题考查了梯形的面积,梯形的面积等于上下底之和乘高除2。
22.(1)见详解
(2)见详解
(3)A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【分析】(1)根据平行四边形的面积计算公式找出符合条件的底和高;
(2)根据梯形的面积和高,找出出上底和下底的关系,计算符合条件的上下底;
(3)数对表示位置的方法:先写列数再写行数,中间用逗号隔开,如:(列数,行数),括号前面标注点的名称即可。
【详解】(1)平行四边形面积为15平方厘米,则底为5厘米,高为3厘米(答案不唯一)
(2)梯形的面积是12平方厘米、高是3厘米,上底+下底=12×2÷3=8(厘米),上底为2厘米,下底为6厘米(答案不唯一)
(3)平行四边形各顶点位置表示为:A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【点睛】灵活运用平行四边形和梯形的面积公式是解答题目的关键。
23.4550根
【分析】根据题意,最上层有38根,最下层有102根,共65层,根据梯形的面积公式:S=(a+b)×h÷2,代入数据解答即可
【详解】(102+38)×65÷2
=140×65÷2
=9100÷2
=4550(根)
答:这堆钢管共有4550根。
【点睛】此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题。
24.84平方米
【分析】面积减少的部分是一个三角形,所以三角形的面积是20平方米,三角形的底是5米。据此,先求出三角形的高。根据题意,三角形的高和正方形的边长相等。据此求出正方形的面积。最后,用正方形的面积加上三角形的面积,求出梯形的面积即可。
【详解】20×2÷5=8(米)
8×8+20
=64+20
=84(平方米)
答:原来梯形的面积是84平方米。
【点睛】本题考查了梯形的面积,本题中,梯形的面积等于三角形的面积加上正方形的面积,其中,三角形的面积等于底乘高除2,正方形的面积等于边长乘边长。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
重点专题:梯形的面积(专项训练)数学五年级上册苏教版
一、选择题
1.两个完全一样的直角三角形重叠成如图形状,形成两个梯形(阴影部分),这两个梯形的面积大小关系是( )。
A.B大 B.A大 C.相等 D.无法确定
2.在下图中,平行线之间的三个图形的面积相比,正确的是( )。
A.平行四边形的面积最大 B.三角形的面积最大
C.梯形的面积最大 D.三个图形的面积都相等
3.用一条线段把一个平行四边形任意分割成两个梯形,这两个梯形中( )总是相等的。
A.高 B.上底、下底之和 C.周长 D.面积
4.一个等腰梯形的周长是48cm,面积是96cm2,高是8cm,则腰长是( )厘米。
A.6 B.8 C.12 D.24
5.一个直角梯形,下底长7cm。上底增加4cm,这个直角梯形就正好变成一个长方形,同时面积增加7cm2。这个直角梯形的面积是( )cm2。
A.14.5 B.17.5 C.20.5
6.梯形的上底扩大到原来的2倍,下底也扩大到原来的2倍,高不变,那么它的面积( )。
A.扩大到原来的2倍 B.扩大到原来的4倍
C.扩大到原来的8倍 D.无法判断
二、填空题
7.一个梯形的上、下底之和是36分米,是高的4倍,这个梯形的面积是 ( )平方分米。
8.一个直角梯形的上底、下底和高分别是10dm、12dm和8dm,它的面积是( )dm2;在梯形内画一个最大的正方形,正方形的面积是( )dm2。
9.下图中,梯形上底长20厘米,高4厘米,阴影部分面积是( )平方厘米。
10.下面梯形的面积是( )dm2。
11.一个梯形的上底是3.2厘米,下底是6.8厘米,面积是40平方厘米,高是( )厘米。
12.一个果园是梯形。它的上底是120米,下底是40米,高是80米。这个果园的面积是( )平方米。
三、判断题
13.两个面积相等的梯形一定能拼成一个平行四边形。( )
14.梯形的面积是平行四边形面积的一半。( )
15.梯形的上底下底越长,面积越大。( )
16.可以把梯形转化成三角形推导出面积公式. ( )
17.一个梯形的高不变,如果上底增加2cm,下底减少2cm,面积不变。( )
四、图形计算
18.求阴影部分面积。(单位:m)
19.下图中阴影部分是一块草坪的平面图,求这块草坪的面积。
五、解答题
20.用100米长的篱笆一面靠墙围成一个花圃(如图)。这个花圃的面积是多少?
21.惠民广场有一个梯形花坛(如下图)。如果每平方米花坛种花16株,这个花坛一共可种花多少株?
22.下面每个小方格的边长都表示1厘米,请你按要求画图。
(1)画出一个面积是15平方厘米的平行四边形。
(2)画一个面积是12平方厘米、高是3厘米的梯形。
(3)用数对表示平行四边形各个顶点的位置。
23.一堆钢管,堆成梯形状,最下层102根,最上层38根,共堆有65层,这堆钢管共有多少根?
24.一个梯形,若把它的下底缩短5cm,就变成一个正方形,且面积减少。原来梯形的面积是多少平方米?
参考答案:
1.C
【分析】由题干可知,梯形A的面积=直角三角形面积-重叠部分面积,梯形B的面积=直角三角形面积-重叠部分面积,故梯形A的面积和梯形B的面积相等,据此解答。
【详解】由分析得,这两个梯形的面积的大小关系是:它们的面积相等。
故答案为:C
【点睛】此题考查的是平面图形面积的比较,解答此题应注意两个完全一样的直角三角形重叠一部分这一条件。
2.D
【分析】由图可知,平行四边形、三角形、梯形的高相等,利用“平行四边形的面积=底×高”“三角形的面积=底×高÷2”“梯形的面积=(上底+下底)×高÷2”求出三个图形的面积,最后比较大小,据此解答。
【详解】假设平行四边形、三角形、梯形的高为h。
平行四边形的面积:4h
三角形的面积:8h÷2=4h
梯形的面积:(2+6)h÷2
=8h÷2
=4h
因为4h=4h=4h,所以三个图形的面积相等。
故答案为:D
【点睛】掌握平行四边形、三角形、梯形的面积计算公式是解答题目的关键。
3.A
【分析】根据梯形高的定义知,梯形是只有一组对边平行的四边形,梯形的高是指上底和下底之间的距离,把平行四边形任意分割成两个梯形时,两平行线之间距离是相等的,据此解答。
【详解】根据以上分析,把一个平行四边形任意分割成两个梯形,其中的高一定相等。
故答案为:A
【点睛】此题是考查平行四边形的特征,掌握平行四边形是两组对边平行,它们之间的距离总是相等是解题关键。
4.C
【分析】根据“梯形的上底+下底=梯形的面积×2÷高”,据此求出上底与下底的和,用周长减去上底与下底的和,再除以2即可求出腰长多少厘米。
【详解】96×2÷8
=192÷8
=24(厘米);
(48-24)÷2
=24÷2
=12(厘米);
故答案为:C。
【点睛】熟练掌握梯形面积和周长的公式并能灵活利用是解答本题的关键。
5.B
【分析】,增加的是三角形,根据三角形的高=面积×2÷底,求出三角形的高,即梯形的高,根据梯形面积=(上底+下底)×高÷2,计算即可。
【详解】7×2÷4=3.5(厘米)
7-4=3(厘米)
(3+7)×3.5÷2
=10×3.5÷2
=17.5(平方厘米)
故答案为:B
【点睛】关键是确定梯形的上底和高,掌握梯形和三角形面积公式。
6.A
【分析】梯形的上下底同时扩大到原来的2倍,高不变,则梯形的面积也扩大到原来的2倍。
【详解】假设原来梯形的上底是2cm,下底是4cm,高是3cm,则现在梯形的上底是4cm,下底是8cm,高是3cm,
原来梯形的面积:(2+4)×3÷2=6×3÷2=9(平方厘米)
现在梯形的面积:(4+8)×3÷2=12×3÷2=18(平方厘米)
18÷9=2,则现在梯形的面积比原来梯形的面积扩大了2倍。
故答案为:A
【点睛】运用梯形的面积计算公式表示出原来的面积和现在的面积,并计算出扩大的倍数是解答本题的关键。
7.162
【分析】根据题意,梯形的上、下底之和是高的4倍,用上、下底之和除以4,即是梯形的高;然后根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】高:36÷4=9(分米)
面积:
36×9÷2
=324÷2
=162(平方分米)
这个梯形的面积是162平方分米。
【点睛】先求出梯形的高,再根据梯形的面积公式求解。
8. 88 64
【分析】根据公式:梯形面积=(上底+下底)×高÷2,代入数据计算即可;在梯形内画一个最大的正方形,那么这个正方形的边长与短边高相等,再用公式:正方形的面积=边长×边长,计算出面积即可,据此解答。
【详解】(10+12)×8÷2
=22×8÷2
=176÷2
=88(dm2)
8×8=64(dm2)
一个直角梯形的上底、下底和高分别是10dm、12dm和8dm,它的面积是88dm2;在梯形内画一个最大的正方形,正方形的面积是64dm2。
【点睛】此题考查了梯形的面积计算以及正方形的面积计算,关键能够结合条件理解如何画最大的正方形。
9.80
【分析】从图中可以看出,阴影部分是两个平行四边形,它们的高都等于梯形的高,它们的底相加等于梯形的上底,所以阴影部分可以看作是一个底为20厘米,高为4的平行四边形;根据平行四边形的面积=底×高,代入数据计算即可。
【详解】20×4=80(平方厘米)
【点睛】把两个阴影部分看成一个平行四边形,找到这个平行四边形与梯形的关系,以及掌握平行四边形的面积公式是解题的关键。
10.
【分析】依据梯形的面积公式求解即可。
【详解】梯形面积=(上底+下底)×高÷2
【点睛】此题的解题关键是掌握梯形的面积公式,依据公式即可求出答案。
11.8
【分析】变换梯形面积计算公式:高=面积×2÷(上底+下底),依此公式计算即可。
【详解】40×2÷(3.2+6.8)
=80÷10
=8(厘米)
【点睛】本题关键在于对梯形面积计算公式的理解。
12.6400
【分析】根据梯形面积=(上底+下底)×高÷2,列式计算即可。
【详解】(120+40)×80÷2
=160×40
=6400(平方米)
【点睛】关键是掌握梯形的面积公式。
13.×
【分析】两个完全一样的梯形才能拼成平行四边形,两个面积相等的梯形不一定完全相同,所以面积相等的梯形不一定能拼成一个平行四边形,据此判断。
【详解】由分析可知:
两个面积相等的梯形一定能拼成一个平行四边形。原题干说法错误。
故答案为:×
【点睛】本题考查梯形和平行四边形的特征,明确它们的特征是解题的关键。
14.×
【分析】根据梯形的面积公式和平行四边形面积公式可以进行推理。
【详解】梯形面积公式是(上底+下底)×高÷2;平行四边形面积公式是底×高;若不知道二者底和高的大小关系,是没办法比较其面积大小的。
故答案为:×
【点睛】两个完全一样的梯形可以拼成一个平行四边形,此时梯形的面积等于所拼成的平行四边形面积的一半。
15.×
【分析】梯形的面积=(上底+下底)×高÷2,梯形的面积和梯形的上底、下底和高都有关系,所以梯形的上底下底越长,面积越大的说法是不正确的。
【详解】据分析知,“梯形的上底下底越长,面积越大”的说法是不正确的。
故答案为:×
【点睛】掌握并灵活运用梯形的面积公式,这是解决此题的关键。
16.
【详解】略
17.√
【详解】略
18.120m2
【分析】如图作辅助线,阴影部分被分成了2个三角形和一个梯形,计算出三个图形的面积之和即可。
【详解】
(7+10)×10÷2+7×7÷2+7×(10-7)÷2
=17×10÷2+7×7÷2+7×3÷2
=85+24.5+10.5
=120(m2)
19.375平方米
【分析】观察图形可知,阴影部分的面积=长方形的面积-梯形的面积,据此代入数值进行计算即可。
【详解】20×30-(20+30)×9÷2
=600-450÷2
=600-225
=375(平方米)
20.1050平方米
【分析】根据题图可知,花圃的形状为梯形,梯形上底与下底的和加上高为100米,用100-30即可求出梯形上底与下底和,再根据“梯形的面积=(上底+下底)×高÷2”解答即可。
【详解】(100-30)×30÷2
=70×30÷2
=1050(平方米);
答:这个花圃的面积是1050平方米。
【点睛】明确梯形上底与下底和是解答本题的关键,再根据梯形的面积公式解答。
21.336株
【分析】根据梯形的面积公式,先计算出这个梯形的面积,再将其乘16,求出这个花坛一共可种花多少株。
【详解】(4+10)×3÷2×16
=14×3÷2×16
=336(株)
答:这个花坛一共可种花336株。
【点睛】本题考查了梯形的面积,梯形的面积等于上下底之和乘高除2。
22.(1)见详解
(2)见详解
(3)A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【分析】(1)根据平行四边形的面积计算公式找出符合条件的底和高;
(2)根据梯形的面积和高,找出出上底和下底的关系,计算符合条件的上下底;
(3)数对表示位置的方法:先写列数再写行数,中间用逗号隔开,如:(列数,行数),括号前面标注点的名称即可。
【详解】(1)平行四边形面积为15平方厘米,则底为5厘米,高为3厘米(答案不唯一)
(2)梯形的面积是12平方厘米、高是3厘米,上底+下底=12×2÷3=8(厘米),上底为2厘米,下底为6厘米(答案不唯一)
(3)平行四边形各顶点位置表示为:A(2,5),B(7,5),C(6,2),D(1,2)(答案不唯一)
【点睛】灵活运用平行四边形和梯形的面积公式是解答题目的关键。
23.4550根
【分析】根据题意,最上层有38根,最下层有102根,共65层,根据梯形的面积公式:S=(a+b)×h÷2,代入数据解答即可
【详解】(102+38)×65÷2
=140×65÷2
=9100÷2
=4550(根)
答:这堆钢管共有4550根。
【点睛】此题主要考查梯形的面积计算方法,能够根据梯形的面积计算方法解决有关的实际问题。
24.84平方米
【分析】面积减少的部分是一个三角形,所以三角形的面积是20平方米,三角形的底是5米。据此,先求出三角形的高。根据题意,三角形的高和正方形的边长相等。据此求出正方形的面积。最后,用正方形的面积加上三角形的面积,求出梯形的面积即可。
【详解】20×2÷5=8(米)
8×8+20
=64+20
=84(平方米)
答:原来梯形的面积是84平方米。
【点睛】本题考查了梯形的面积,本题中,梯形的面积等于三角形的面积加上正方形的面积,其中,三角形的面积等于底乘高除2,正方形的面积等于边长乘边长。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
