人教版小学数学六年级下册2.《数学分数、百分数的认识》课件(共40张PPT)
文档属性
| 名称 | 人教版小学数学六年级下册2.《数学分数、百分数的认识》课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 21:47:01 | ||
图片预览









文档简介
(共40张PPT)
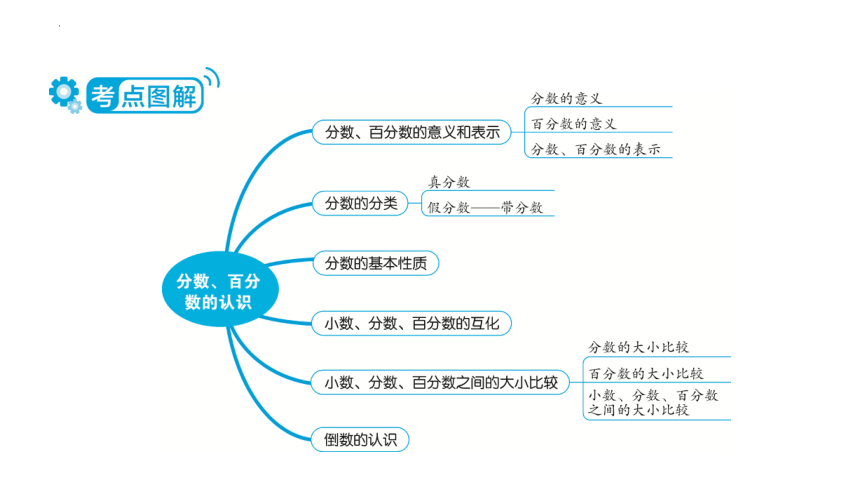
分数、百分数的认识
考点1 分数、百分数的意义和表示
考点精讲
1. 分数的意义
(1)把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
(2)把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位。
2. 百分数的意义
表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常不写成分数形式,而是在原来的分子后面加上百分号“%”来表示,读作“百分之……”。
3. 分数和除法的关系
除法是一种运算,有运算符号;分数是一种数。因此,一般应叙述为被除数相当于分子,而不能说成被除数就是分子。
分数与除法的联系与区别∶
联系 区别
分数 分子 分数线 分母 分数是一个数,可以看作两个数相除
除法 被除数 除号 除数 除法是一种运算
真题精讲
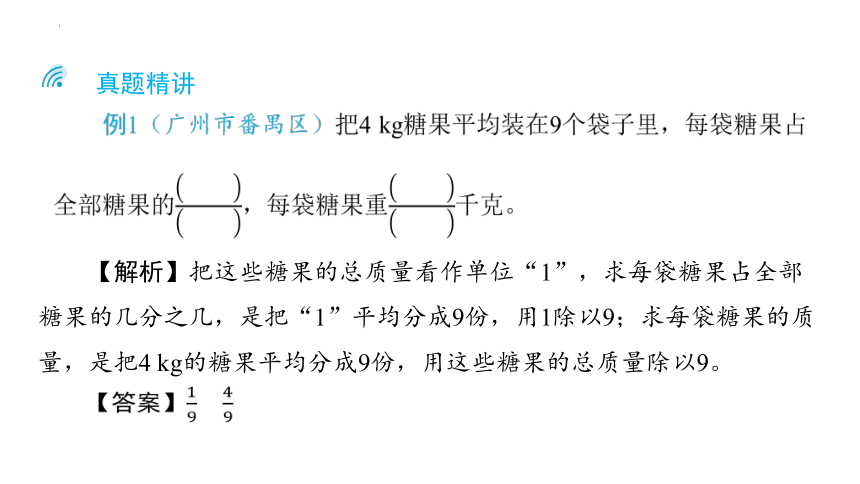
例1(广州市番禺区)把4 kg糖果平均装在9个袋子里,每袋糖果占全部糖果的,每袋糖果重千克。
【解析】把这些糖果的总质量看作单位“1”,求每袋糖果占全部糖果的几分之几,是把“1”平均分成9份,用1除以9;求每袋糖果的质量,是把4 kg的糖果平均分成9份,用这些糖果的总质量除以9。
【答案】
例2(洛阳市偃师市)科学兴趣组用50粒玉米种子做发芽试验,结果7粒没发芽。玉米种子的发芽率是( ) %。
【解析】发芽率是指发芽种子数占种子总数的百分比,计算方法是∶ 发芽种子数÷种子总数×100%, 则该种子的发芽率为(50-7)÷50×100%=86%。
【答案】86
跟踪训练
1. 将一根4米长的铁丝平均分成5段,每段是全长的( ),每段长( )米。
2. 的分数单位是( ),再加上( 11 )个这样的分数单位就是最小的质数。
3. (惠州市惠阳区)一件商品降价10%,这里的10%是指( 降的价格 )是( 原价 )的10%。
11
降的价
格
原价
考点2 分数的分类
考点精讲
分数的分类
1. 真分数∶分子比分母小的分数叫做真分数。真分数小于1。
2. 假分数∶分子大于或等于分母的分数,叫做假分数。假分数大于或等于1。
3. 带分数∶由一个整数和一个真分数合成的数,叫做带分数。假分数可以化成带分数或整数。
真题精讲
例(汕尾市)在下面的□中依次填上真分数、带分数和假分数。
【解析】把0到1平均分成5份,则每份表示,据此数出各方框对应的分数中含有多少个,并以此用真分数、带分数和假分数表示出来,据此解答。
【答案】 1
跟踪训练
1. (珠海市)若是假分数,是真分数,则整数a应是( 16 )。
2. (清远市)将带分数化成假分数,例如∶3==,a,b,c表示的数依次为( C )。
A. 3,2,1 B. 5,3,18 C. 5,2,17
16
C
考点3 分数的基本性质
考点精讲
1. 分数的基本性质
分数的分子和分母都乘以或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质,它是约分和通分的依据。
2. 约分和通分
(1)最简分数∶分子、分母是互质数的分数,叫做最简分数。
(2)约分∶把一个分数化成同它相等但分子、分母都比较小的分数,叫做约分。
约分的方法∶用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止。
(3)通分∶把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分的方法∶先求出原来几个分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。
真题精讲
例1(湛江市赤坎区)的分子扩大到原来的3倍,要使分数的大小不变,分母应该加( )。
【解析】原分数分子是2,现在分数的分子扩大到原来的3倍,原分数分母是7,要使前后分数大小相等,分母也应扩大到原来的3倍,变为21,即21=7+14。
【答案】14
例2(宁波市江北区)(a是非零自然数)是一个最简真分数,那么a的取值有( )个。
A. 1 B. 2 C. 3 D. 4
【解析】根据真分数的定义,分子小于分母的分数是真分数,再找出小于8的数中与8互质的数即可确定最简真分数。这个最简真分数可以是,,,,一共4个。
【答案】D
跟踪训练
1. (广州市)的分母加上27,要使分数的大小不变,分子应( C )。
A. 加上27 B. 除以4 C. 乘4 D. 乘3
2. (汕头市)在,,中,与大小相等的数有( )。
3. (黄冈市红安县)分母为12的最简真分数有( 4 )个,它们的和是( 2 )。
C
4
2
考点4 小数、分数、百分数的互化
考点精讲
小数、分数、百分数的互化
真题精讲
例(揭阳市普宁市)3÷( )=0.75=15∶( )==( )%。
【解析】把0.75化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系,=3÷4;根据比与分数的关系,=3∶4,再根据比的基本性质,比的前、后项都乘5就是15∶20;把0.75的小数点向右移动两位添上百分号就是75%。
【答案】4 20 12 75
跟踪训练
1. (阳江市)24÷( 40 )=0.6==( 18 )∶30=( 60 )%
40
18
60
=9∶( 36 )=( 6 )÷24=( 25 )%=( 0.25 ) (填小数)。
36
6
25
0.25
2. (深圳市)根据如图中的阴影部分与整个图形的关系将下边的等式填写完整。
2
考点5 小数、分数、百分数之间的大小比较
考点精讲
1. 比较分数的大小
(1)分母相同的分数,分子大的那个分数就大。
(2)分子相同的分数,分母小的那个分数就大。
(3)分母和分子都不同的分数,通常是先通分,转化成同分母的分数,再比较大小。
(4)如果被比较的分数是带分数,先要比较它们的整数部分,整数部分大的那个带分数就大;如果整数部分相同,再比较它们的分数部分,分数部分大的那个带分数就大。
2. 比较百分数的大小
直接比较百分号前的数的大小即可。
3.小数、分数、百分数之间的大小比较
小数、分数、百分数之间不能直接比较大小,通常都先化成小数,再比较。
真题精讲
例(阳江市)在3.14%,3.14,3.,π,这5个数中,最大的数是( ),最小的数是( )。
【解析】因为3.14%=0.0314,π≈3.1416,≈3.1429,且3.1429>3.1416>3.>3.14>0.0314,即>π>3.>3.14>3.14%,所以最大的数是,最小的数是3.14%。
【答案】 3.14%
跟踪训练
1. 在 里填上“>”“<”或“=”。
= 75% 4 < < 1.5
2. 在0.27,0.,,27.3%,中,最大的数是( ),最小的数是( 0.27 )。
=
<
<
0.27
>
考点6 倒数的认识
考点精讲
倒数
1.乘积是1的两个数互为倒数。
2.求一个数(0除外)的倒数,只要把这个数的分子、分母调换位置。
3.1的倒数是1,0没有倒数。
真题精讲
例(深圳市光明区)因为2×=1,所以( )。
A. 2是倒数 B. 是倒数
C. 2和互为倒数 D. 2和都是倒数
【解析】若两个数的乘积是1,我们就称这两个数互为倒数,不能说哪一个数是倒数,据此判断即可。
【答案】C
跟踪训练
1. 下面各组数中,互为倒数的是( C )。
A. 和 B. 和 C. 和3 D. 1和
2. (东莞市)已知数a的倒数大于1,那么数a一定是( A )。
A. 真分数 B. 假分数
C. 带分数 D. 非0的整数
C
A
一、填空题。
1. ( )×5=( )×=( 4 )×0.25=1×( )=1。
2. (深圳市)===( 4 )÷5=( 0.8 )(填小数)。
4
4
0.8
45
16
3. (东莞市)2的分数单位是( ),再加上( 5 )个这样的分数单位就是最小的合数。
4. 在数轴上面的□里填上假分数,在下面的□里填上带分数。
5
5. (韶关市)“五一”期间,某市接待游客比去年同期增长38.2%,其中一日游的游客数占游客总量的百分之六十九点四九。38.2%读作( 百分之三十八点二 ),百分之六十九点四九写作( 69.49% )。
6. (郴州市宜章县)在3.303,3,333%,3.31中,最大的数是( 3 ),最小的数是( 3.303 )。
7. 如图阴影部分用小数表示是( 0.25 ),用百分数表示是( 25 )%。
百分之三十八点二
69.49%
3
3.303
0.25
25
8. (揭阳市惠来县)一个10分钟的沙漏计时器,里面共装沙45克,1分钟可以漏下这些沙的( ),漏下这些沙的需要( 7.5 )分钟。
7.5
二、选择题。
1. (深圳市)下列问题,不可能用100%表示的是( B )。
A. 六(1)班学生今天的出勤率
B. 一批优质大豆的出油率
C. 一批产品的合格率
D. 张叔叔种植一批树苗的成活率
2. 要使是真分数,是假分数,“*”应该是( A )。
A. 7 B. 8 C. 9 D. 10
B
A
3. (韶关市)的分子增加12,要使分数的大小不变,分母应( C )。
A. 也增加12
B. 扩大到原来的3倍
C. 增加27
4. (襄阳市樊城区)把2米长的绳子平均剪成5段,每段绳长是全长的( C )。
A. B. 40% C. 20% D.
C
C
5. (广州市)四个小朋友探究步长(平均每步的长度)∶王华1步走0.75米,李奇5步走3米,张娟5步走4米,赵兰8步走7米。谁的步长最长?( D )。
A. 王华 B. 李奇
C. 张娟 D. 赵兰
D
三、判断题。(对的画“√”,错的画“×”)
1. (日照市东港区)把26%的百分号去掉,这个数就扩大到原来的100倍。 ( √ )
2. 一件衣服打九折就是降价10%。 ( √ )
3. (黄石市大冶市)一条路修了千米,也就是修了89%千米。 ( × )
4. (揭阳市揭东区)分数的分母越大,它的分数单位就越大。 ( × )
5. 大于而小于的最简分数不存在。 ( × )
√
√
×
×
×
四、在图中,用阴影部分表示下面的百分数。
五、录入同样一份稿件,甲打字员用了小时,乙打字员用了0.35小时,丙打字员用了20分钟,哪位打字员的速度快些?
小时=0.25小时
20分钟=小时=小时=0.小时
0.25<0.<0.35
所以甲打字员的速度快些。
六、把一个分数约分,先用5约了一次,再用3约了两次,得。原来这个分数是多少?
分子∶1×3×3×5=45;分母∶2×3×3×5=90;原来这个分数是。
七、 有四个不同的偶数,它们的倒数的和是1,知道其中两个数是2和4,其余两个数分别是几?
+=,1-=,=,=+=+,因此,其余两个偶数是6和12。
分数、百分数的认识
考点1 分数、百分数的意义和表示
考点精讲
1. 分数的意义
(1)把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
(2)把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位。
2. 百分数的意义
表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常不写成分数形式,而是在原来的分子后面加上百分号“%”来表示,读作“百分之……”。
3. 分数和除法的关系
除法是一种运算,有运算符号;分数是一种数。因此,一般应叙述为被除数相当于分子,而不能说成被除数就是分子。
分数与除法的联系与区别∶
联系 区别
分数 分子 分数线 分母 分数是一个数,可以看作两个数相除
除法 被除数 除号 除数 除法是一种运算
真题精讲
例1(广州市番禺区)把4 kg糖果平均装在9个袋子里,每袋糖果占全部糖果的,每袋糖果重千克。
【解析】把这些糖果的总质量看作单位“1”,求每袋糖果占全部糖果的几分之几,是把“1”平均分成9份,用1除以9;求每袋糖果的质量,是把4 kg的糖果平均分成9份,用这些糖果的总质量除以9。
【答案】
例2(洛阳市偃师市)科学兴趣组用50粒玉米种子做发芽试验,结果7粒没发芽。玉米种子的发芽率是( ) %。
【解析】发芽率是指发芽种子数占种子总数的百分比,计算方法是∶ 发芽种子数÷种子总数×100%, 则该种子的发芽率为(50-7)÷50×100%=86%。
【答案】86
跟踪训练
1. 将一根4米长的铁丝平均分成5段,每段是全长的( ),每段长( )米。
2. 的分数单位是( ),再加上( 11 )个这样的分数单位就是最小的质数。
3. (惠州市惠阳区)一件商品降价10%,这里的10%是指( 降的价格 )是( 原价 )的10%。
11
降的价
格
原价
考点2 分数的分类
考点精讲
分数的分类
1. 真分数∶分子比分母小的分数叫做真分数。真分数小于1。
2. 假分数∶分子大于或等于分母的分数,叫做假分数。假分数大于或等于1。
3. 带分数∶由一个整数和一个真分数合成的数,叫做带分数。假分数可以化成带分数或整数。
真题精讲
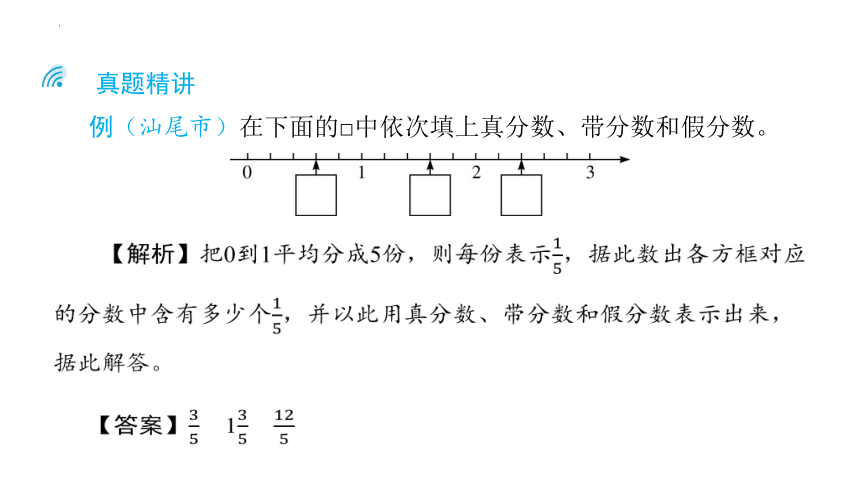
例(汕尾市)在下面的□中依次填上真分数、带分数和假分数。
【解析】把0到1平均分成5份,则每份表示,据此数出各方框对应的分数中含有多少个,并以此用真分数、带分数和假分数表示出来,据此解答。
【答案】 1
跟踪训练
1. (珠海市)若是假分数,是真分数,则整数a应是( 16 )。
2. (清远市)将带分数化成假分数,例如∶3==,a,b,c表示的数依次为( C )。
A. 3,2,1 B. 5,3,18 C. 5,2,17
16
C
考点3 分数的基本性质
考点精讲
1. 分数的基本性质
分数的分子和分母都乘以或者除以相同的数(0除外),分数的大小不变,这叫做分数的基本性质,它是约分和通分的依据。
2. 约分和通分
(1)最简分数∶分子、分母是互质数的分数,叫做最简分数。
(2)约分∶把一个分数化成同它相等但分子、分母都比较小的分数,叫做约分。
约分的方法∶用分子和分母的公约数(1除外)去除分子、分母;通常要除到得出最简分数为止。
(3)通分∶把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
通分的方法∶先求出原来几个分母的最小公倍数,然后把各分数化成用这个最小公倍数作分母的分数。
真题精讲
例1(湛江市赤坎区)的分子扩大到原来的3倍,要使分数的大小不变,分母应该加( )。
【解析】原分数分子是2,现在分数的分子扩大到原来的3倍,原分数分母是7,要使前后分数大小相等,分母也应扩大到原来的3倍,变为21,即21=7+14。
【答案】14
例2(宁波市江北区)(a是非零自然数)是一个最简真分数,那么a的取值有( )个。
A. 1 B. 2 C. 3 D. 4
【解析】根据真分数的定义,分子小于分母的分数是真分数,再找出小于8的数中与8互质的数即可确定最简真分数。这个最简真分数可以是,,,,一共4个。
【答案】D
跟踪训练
1. (广州市)的分母加上27,要使分数的大小不变,分子应( C )。
A. 加上27 B. 除以4 C. 乘4 D. 乘3
2. (汕头市)在,,中,与大小相等的数有( )。
3. (黄冈市红安县)分母为12的最简真分数有( 4 )个,它们的和是( 2 )。
C
4
2
考点4 小数、分数、百分数的互化
考点精讲
小数、分数、百分数的互化
真题精讲
例(揭阳市普宁市)3÷( )=0.75=15∶( )==( )%。
【解析】把0.75化成分数并化简是,根据分数的基本性质,分子、分母都乘4就是;根据分数与除法的关系,=3÷4;根据比与分数的关系,=3∶4,再根据比的基本性质,比的前、后项都乘5就是15∶20;把0.75的小数点向右移动两位添上百分号就是75%。
【答案】4 20 12 75
跟踪训练
1. (阳江市)24÷( 40 )=0.6==( 18 )∶30=( 60 )%
40
18
60
=9∶( 36 )=( 6 )÷24=( 25 )%=( 0.25 ) (填小数)。
36
6
25
0.25
2. (深圳市)根据如图中的阴影部分与整个图形的关系将下边的等式填写完整。
2
考点5 小数、分数、百分数之间的大小比较
考点精讲
1. 比较分数的大小
(1)分母相同的分数,分子大的那个分数就大。
(2)分子相同的分数,分母小的那个分数就大。
(3)分母和分子都不同的分数,通常是先通分,转化成同分母的分数,再比较大小。
(4)如果被比较的分数是带分数,先要比较它们的整数部分,整数部分大的那个带分数就大;如果整数部分相同,再比较它们的分数部分,分数部分大的那个带分数就大。
2. 比较百分数的大小
直接比较百分号前的数的大小即可。
3.小数、分数、百分数之间的大小比较
小数、分数、百分数之间不能直接比较大小,通常都先化成小数,再比较。
真题精讲
例(阳江市)在3.14%,3.14,3.,π,这5个数中,最大的数是( ),最小的数是( )。
【解析】因为3.14%=0.0314,π≈3.1416,≈3.1429,且3.1429>3.1416>3.>3.14>0.0314,即>π>3.>3.14>3.14%,所以最大的数是,最小的数是3.14%。
【答案】 3.14%
跟踪训练
1. 在 里填上“>”“<”或“=”。
= 75% 4 < < 1.5
2. 在0.27,0.,,27.3%,中,最大的数是( ),最小的数是( 0.27 )。
=
<
<
0.27
>
考点6 倒数的认识
考点精讲
倒数
1.乘积是1的两个数互为倒数。
2.求一个数(0除外)的倒数,只要把这个数的分子、分母调换位置。
3.1的倒数是1,0没有倒数。
真题精讲
例(深圳市光明区)因为2×=1,所以( )。
A. 2是倒数 B. 是倒数
C. 2和互为倒数 D. 2和都是倒数
【解析】若两个数的乘积是1,我们就称这两个数互为倒数,不能说哪一个数是倒数,据此判断即可。
【答案】C
跟踪训练
1. 下面各组数中,互为倒数的是( C )。
A. 和 B. 和 C. 和3 D. 1和
2. (东莞市)已知数a的倒数大于1,那么数a一定是( A )。
A. 真分数 B. 假分数
C. 带分数 D. 非0的整数
C
A
一、填空题。
1. ( )×5=( )×=( 4 )×0.25=1×( )=1。
2. (深圳市)===( 4 )÷5=( 0.8 )(填小数)。
4
4
0.8
45
16
3. (东莞市)2的分数单位是( ),再加上( 5 )个这样的分数单位就是最小的合数。
4. 在数轴上面的□里填上假分数,在下面的□里填上带分数。
5
5. (韶关市)“五一”期间,某市接待游客比去年同期增长38.2%,其中一日游的游客数占游客总量的百分之六十九点四九。38.2%读作( 百分之三十八点二 ),百分之六十九点四九写作( 69.49% )。
6. (郴州市宜章县)在3.303,3,333%,3.31中,最大的数是( 3 ),最小的数是( 3.303 )。
7. 如图阴影部分用小数表示是( 0.25 ),用百分数表示是( 25 )%。
百分之三十八点二
69.49%
3
3.303
0.25
25
8. (揭阳市惠来县)一个10分钟的沙漏计时器,里面共装沙45克,1分钟可以漏下这些沙的( ),漏下这些沙的需要( 7.5 )分钟。
7.5
二、选择题。
1. (深圳市)下列问题,不可能用100%表示的是( B )。
A. 六(1)班学生今天的出勤率
B. 一批优质大豆的出油率
C. 一批产品的合格率
D. 张叔叔种植一批树苗的成活率
2. 要使是真分数,是假分数,“*”应该是( A )。
A. 7 B. 8 C. 9 D. 10
B
A
3. (韶关市)的分子增加12,要使分数的大小不变,分母应( C )。
A. 也增加12
B. 扩大到原来的3倍
C. 增加27
4. (襄阳市樊城区)把2米长的绳子平均剪成5段,每段绳长是全长的( C )。
A. B. 40% C. 20% D.
C
C
5. (广州市)四个小朋友探究步长(平均每步的长度)∶王华1步走0.75米,李奇5步走3米,张娟5步走4米,赵兰8步走7米。谁的步长最长?( D )。
A. 王华 B. 李奇
C. 张娟 D. 赵兰
D
三、判断题。(对的画“√”,错的画“×”)
1. (日照市东港区)把26%的百分号去掉,这个数就扩大到原来的100倍。 ( √ )
2. 一件衣服打九折就是降价10%。 ( √ )
3. (黄石市大冶市)一条路修了千米,也就是修了89%千米。 ( × )
4. (揭阳市揭东区)分数的分母越大,它的分数单位就越大。 ( × )
5. 大于而小于的最简分数不存在。 ( × )
√
√
×
×
×
四、在图中,用阴影部分表示下面的百分数。
五、录入同样一份稿件,甲打字员用了小时,乙打字员用了0.35小时,丙打字员用了20分钟,哪位打字员的速度快些?
小时=0.25小时
20分钟=小时=小时=0.小时
0.25<0.<0.35
所以甲打字员的速度快些。
六、把一个分数约分,先用5约了一次,再用3约了两次,得。原来这个分数是多少?
分子∶1×3×3×5=45;分母∶2×3×3×5=90;原来这个分数是。
七、 有四个不同的偶数,它们的倒数的和是1,知道其中两个数是2和4,其余两个数分别是几?
+=,1-=,=,=+=+,因此,其余两个偶数是6和12。
