人教版小学数学六年级下册6.1《因数和倍数》课件(共28张PPT)
文档属性
| 名称 | 人教版小学数学六年级下册6.1《因数和倍数》课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 00:00:00 | ||
图片预览

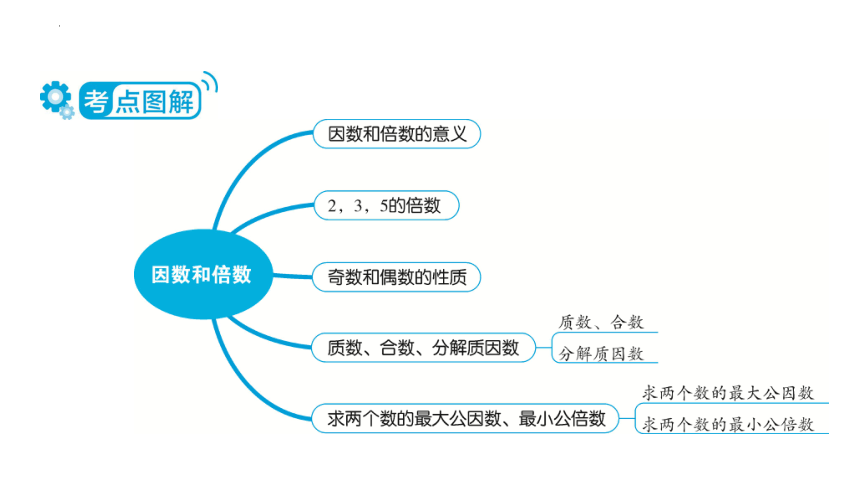







文档简介
(共28张PPT)
因数和倍数
考点1 因数和倍数的意义
考点精讲
1. 如果自然数a和自然数b的乘积是c,即a×b=c(一般不包括0),那么a和b都是c的因数,c是a和b的倍数。倍数和因数是相互依存的。
2. 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
3. 一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
真题精讲
例(梅州市大埔县)在35÷7=5中,( )是( )的倍数,( )是( )的因数。
【解析】在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,据此解答。
【答案】35 5和7 5和7 35
跟踪训练
1. 8×7=56,56是8和7的( 倍数 ),8和7是56的( 因数 )。(填“因数”或“倍数”)
2. (湛江市赤坎区)一个数既是b的倍数,又是b的因数,这个数是( b )。
3. 自然数16的所有因数有( 1,2,4,8,16 ),它的最小倍数是( 16 )。
倍数
因数
b
1,2,4,8,16
16
考点2 2,3,5的倍数
考点精讲
2的倍数特征∶个位上的数字是0,2,4,6,8。
5的倍数特征∶个位上的数字是0或5。
3的倍数特征∶一个数的各位上的数的和是3的倍数,这个数就是3的倍数。
真题精讲
例(中山市)一个四位数7□1□,它能同时被2,3,5整除,这个四位数最大是( )。
【解析】既是2的倍数又是5的倍数,这个数的个位必定是0,要满足被3整除,意味着7+□+1+0的和是3的倍数,当□=7时,可以被3整除且这个四位数最大。据此解答。
【答案】7710
跟踪训练
1. “65□”是一个三位数,当□里填( 0 )时,它既是2的倍数,也是5的倍数;当□里填( 4 )时,它既是3的倍数,又是一个偶数。
2. 2,3,5的公倍数中,最小的两位数是( 30 )。
0
4
30
考点3 奇数和偶数的性质
考点精讲
1.相邻两个自然数之和是奇数,之积是偶数。
2. 奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数;
奇数-奇数=偶数,奇数-偶数=奇数,偶数-奇数=奇数,偶数-偶数=偶数;
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
真题精讲
例(揭阳市揭东区)判断对错∶a是一个偶数,b是一个奇数,2a-3b的值一定是奇数。( )
【解析】a是一个偶数,b是一个奇数,所以2a是偶数,3b是奇数。2a-3b就是一个偶数减去一个奇数,差一定是奇数,所以原题干表述正确。
【答案】√
跟踪训练
1. (江门市开平市)如果m表示自然数,那么偶数可以表示为( A )。
A. 2m B. m-2 C. m+2
2. (福州市晋安区)如果a+1的和是奇数,那么a一定是( B )。
A. 奇数 B. 偶数 C. 质数 D. 合数
A
B
考点4 质数、合数、分解质因数
考点精讲
1. 质数、合数
(1)一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
(2)一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
(3)1既不是质数,也不是合数,最小的质数是2,最小的合数是4。
2. 分解质因数
(1)质因数
每个合数都可以写成几个质数相乘的形式,这几个质数就都叫做这个合数的质因数。例如15=3×5,3和5 叫做15的质因数。
(2)分解质因数
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。通常用短除法来分解质因数。先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
(3)分解质因数的方法∶
①分步分解 ②短除法
30=2×3×5 30=2×3×5
真题精讲
例(广安市)在自然数1 ~ 24中,最大的奇数且又是合数的数是( ),把它写成质数相乘的形式是( )。
【解析】1~24中,最大奇数是23,不是合数;往下找,21是奇数,也是合数,因此21符合题意。把它写成质数相乘的形式是3×7。
【答案】21 3×7
跟踪训练
1. 哥德巴赫猜想被誉为“数学皇冠上的明珠”,内容是“任何大于2的偶数都可以表示成两个质数之和”。比如12=( 5 )+( 7 )。
2. 2的分数单位是( ),再增加( 14 )个这样的分数单位就可以得到最小的合数。
3. 一个数的最大因数是24,这个数是( 24 ),把它分解质因数是( 24=2×2×2×3 )。
5
7
14
24
24=2×2×2×3
考点5 求两个数的最大公因数、最小公倍数
考点精讲
1. 两个数的最大公因数
(1)两个数公有的因数叫做这两个数的公因数。其中最大的一个叫做这两个数的最大公因数。
(2)如果较小数是较大数的因数,那么较小数就是这两个数的最大公因数。
(3)如果两个数是互质数,它们的最大公因数就是1。
2. 两个数的最小公倍数
(1)两个数公有的倍数叫做这两个数的公倍数。其中最小的一个叫做这两个数的最小公倍数。
(2)如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
(3)如果两个数是互质数,那么这两个数的积就是它们的最小公倍数。
(4)两个数的公因数的个数是有限的,而两个数的公倍数的个数是无限的。
真题精讲
例(汕头市金平区)如果a÷b=c(a,b,c均为非零自然数),那么a和b的最大公因数是 ,最小公倍数是 .
【解析】因为a和b是倍数关系,且a>b,所以a和b的最大公因数是b,最小公倍数是a。
【答案】b a
跟踪训练
1. (怀化市通道县)如果A=4B(A,B均不为0),A和B的最小公倍数是( A ),A和B的最大公因数是( B )。
2. 有一包糖果,如果每2颗一堆,正好分完;如果每3颗一堆,也正好分完;如果每5颗一堆,还能正好分完。这包糖果至少有多少颗?
2×3×5=30(颗)
A
B
一、填空题。
1. 冬季奥林匹克运动会,简称为冬奥会,它是世界上最大的冬季综合性运动会。第一届冬奥会于1924年在法国的夏蒙尼举行。最近的一届冬奥会是第24届冬奥会,于2022年2月4日至2月20日在中国北京和张家口举行。
(1)上面信息出现的自然数中,质数是( 2 ),最大的偶数是( 2022 )。
(2)这些自然数中,既是2的倍数,又是5的倍数的数是( 20 )。
(3)文中的自然数里,有因数3的数有( 2 )个。
2
2022
20
2
2. 15和12的最大公因数是( 3 ),最小公倍数是( 60 )。
3. 填上合适的质数。
40=( 3 )+( 37 )=( 11 )+( 29 )
3
60
3
37
11
29
4. 一个三位数47□,要使它是3的倍数,□里可以填的数有( 1,4,7 );要使它既是3的倍数,又是2的倍数,□里可以填的数有( 4 )。
5. 已知a=2×2×3×5,b=2×5×7,则a和b的最大公因数是( 10 ),最小公倍数是( 420 )。
1,4,
7
4
10
420
6. 从5、2、1、0中选3个数字组成一个同时能被2、3、5整除的最小三位数,并把它分解质因数是( 120=2×2×2×3×5 )。
7. 校运会的开幕式上,五(1)班有男生24人和女生18人参加展演。如果男生和女生要分别排成整行,且每行的人数要相同,每行最多有( 6 )人,一共可以分成( 7 )行。
120=2×2×2×3×5
6
7
二、选择题。
1. 一个长方形的长是奇数,宽是偶数,它的周长一定是( B )。
A. 偶数和质数 B. 偶数和合数
C. 奇数和质数 D. 奇数和合数
2. 下列说法正确的是( D )。
A. 所有的质数都是奇数
B. 两个奇数的差一定是奇数
C. 整数都比分数大
D. 是4的倍数的数一定是偶数
B
D
3. 已知a,b均是大于1的自然数,且a是b的倍数,则下面的说法,错误的是( C )。
A. b是a的因数
B. a是a与b的公倍数
C. a与b的和一定是偶数
D. a与b的积一定不是质数
4. 甲、乙两数的最大公因数是1,最小公倍数是( A )。
A. 甲×乙 B. 甲+乙
C. 甲 D. 乙
C
A
三、解决问题。
1. 某电商平台,一袋大米a元(a为整数),妈妈购了3袋,付钱时妈妈输入265元,小明马上说不对,你觉得对吗?为什么?请说明理由。
妈妈输的不对。
因为妈妈购了3袋大米,所以付的钱数应是3的倍数,265不是3的倍数,所以不对。
2. 张伯伯家厨房长30分米,宽18分米。如果用边长是整分米数的正方形地砖把厨房的地面铺满(使用的地砖要求是整块),地砖的边长最大是几分米?这时需要多少块地砖?
30=2×3×5 18=2×3×3
30和18的最大公因数是∶2×3=6
即正方形地砖的边长最大是6分米。
需要地砖∶30×18÷(6×6)=15(块)
四、 李阿姨到商场买同品牌的桔子饮料,大瓶每瓶6元,小瓶每瓶4元。李阿姨带的钱如果都买小瓶,还剩2元,如果都买大瓶,也剩2元。李阿姨至少带了多少钱?
4=2×2 6=2×3
4和6的最小公倍数是2×2×3=12
至少带了∶12+2=14(元)
因数和倍数
考点1 因数和倍数的意义
考点精讲
1. 如果自然数a和自然数b的乘积是c,即a×b=c(一般不包括0),那么a和b都是c的因数,c是a和b的倍数。倍数和因数是相互依存的。
2. 一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身。
3. 一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数。
真题精讲
例(梅州市大埔县)在35÷7=5中,( )是( )的倍数,( )是( )的因数。
【解析】在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数,据此解答。
【答案】35 5和7 5和7 35
跟踪训练
1. 8×7=56,56是8和7的( 倍数 ),8和7是56的( 因数 )。(填“因数”或“倍数”)
2. (湛江市赤坎区)一个数既是b的倍数,又是b的因数,这个数是( b )。
3. 自然数16的所有因数有( 1,2,4,8,16 ),它的最小倍数是( 16 )。
倍数
因数
b
1,2,4,8,16
16
考点2 2,3,5的倍数
考点精讲
2的倍数特征∶个位上的数字是0,2,4,6,8。
5的倍数特征∶个位上的数字是0或5。
3的倍数特征∶一个数的各位上的数的和是3的倍数,这个数就是3的倍数。
真题精讲
例(中山市)一个四位数7□1□,它能同时被2,3,5整除,这个四位数最大是( )。
【解析】既是2的倍数又是5的倍数,这个数的个位必定是0,要满足被3整除,意味着7+□+1+0的和是3的倍数,当□=7时,可以被3整除且这个四位数最大。据此解答。
【答案】7710
跟踪训练
1. “65□”是一个三位数,当□里填( 0 )时,它既是2的倍数,也是5的倍数;当□里填( 4 )时,它既是3的倍数,又是一个偶数。
2. 2,3,5的公倍数中,最小的两位数是( 30 )。
0
4
30
考点3 奇数和偶数的性质
考点精讲
1.相邻两个自然数之和是奇数,之积是偶数。
2. 奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数;
奇数-奇数=偶数,奇数-偶数=奇数,偶数-奇数=奇数,偶数-偶数=偶数;
奇数×奇数=奇数,奇数×偶数=偶数,偶数×偶数=偶数。
真题精讲
例(揭阳市揭东区)判断对错∶a是一个偶数,b是一个奇数,2a-3b的值一定是奇数。( )
【解析】a是一个偶数,b是一个奇数,所以2a是偶数,3b是奇数。2a-3b就是一个偶数减去一个奇数,差一定是奇数,所以原题干表述正确。
【答案】√
跟踪训练
1. (江门市开平市)如果m表示自然数,那么偶数可以表示为( A )。
A. 2m B. m-2 C. m+2
2. (福州市晋安区)如果a+1的和是奇数,那么a一定是( B )。
A. 奇数 B. 偶数 C. 质数 D. 合数
A
B
考点4 质数、合数、分解质因数
考点精讲
1. 质数、合数
(1)一个数,如果只有1和它本身两个因数,这样的数叫做质数(或素数)。
(2)一个数,如果除了1和它本身还有别的因数,这样的数叫做合数。
(3)1既不是质数,也不是合数,最小的质数是2,最小的合数是4。
2. 分解质因数
(1)质因数
每个合数都可以写成几个质数相乘的形式,这几个质数就都叫做这个合数的质因数。例如15=3×5,3和5 叫做15的质因数。
(2)分解质因数
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。通常用短除法来分解质因数。先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
(3)分解质因数的方法∶
①分步分解 ②短除法
30=2×3×5 30=2×3×5
真题精讲
例(广安市)在自然数1 ~ 24中,最大的奇数且又是合数的数是( ),把它写成质数相乘的形式是( )。
【解析】1~24中,最大奇数是23,不是合数;往下找,21是奇数,也是合数,因此21符合题意。把它写成质数相乘的形式是3×7。
【答案】21 3×7
跟踪训练
1. 哥德巴赫猜想被誉为“数学皇冠上的明珠”,内容是“任何大于2的偶数都可以表示成两个质数之和”。比如12=( 5 )+( 7 )。
2. 2的分数单位是( ),再增加( 14 )个这样的分数单位就可以得到最小的合数。
3. 一个数的最大因数是24,这个数是( 24 ),把它分解质因数是( 24=2×2×2×3 )。
5
7
14
24
24=2×2×2×3
考点5 求两个数的最大公因数、最小公倍数
考点精讲
1. 两个数的最大公因数
(1)两个数公有的因数叫做这两个数的公因数。其中最大的一个叫做这两个数的最大公因数。
(2)如果较小数是较大数的因数,那么较小数就是这两个数的最大公因数。
(3)如果两个数是互质数,它们的最大公因数就是1。
2. 两个数的最小公倍数
(1)两个数公有的倍数叫做这两个数的公倍数。其中最小的一个叫做这两个数的最小公倍数。
(2)如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
(3)如果两个数是互质数,那么这两个数的积就是它们的最小公倍数。
(4)两个数的公因数的个数是有限的,而两个数的公倍数的个数是无限的。
真题精讲
例(汕头市金平区)如果a÷b=c(a,b,c均为非零自然数),那么a和b的最大公因数是 ,最小公倍数是 .
【解析】因为a和b是倍数关系,且a>b,所以a和b的最大公因数是b,最小公倍数是a。
【答案】b a
跟踪训练
1. (怀化市通道县)如果A=4B(A,B均不为0),A和B的最小公倍数是( A ),A和B的最大公因数是( B )。
2. 有一包糖果,如果每2颗一堆,正好分完;如果每3颗一堆,也正好分完;如果每5颗一堆,还能正好分完。这包糖果至少有多少颗?
2×3×5=30(颗)
A
B
一、填空题。
1. 冬季奥林匹克运动会,简称为冬奥会,它是世界上最大的冬季综合性运动会。第一届冬奥会于1924年在法国的夏蒙尼举行。最近的一届冬奥会是第24届冬奥会,于2022年2月4日至2月20日在中国北京和张家口举行。
(1)上面信息出现的自然数中,质数是( 2 ),最大的偶数是( 2022 )。
(2)这些自然数中,既是2的倍数,又是5的倍数的数是( 20 )。
(3)文中的自然数里,有因数3的数有( 2 )个。
2
2022
20
2
2. 15和12的最大公因数是( 3 ),最小公倍数是( 60 )。
3. 填上合适的质数。
40=( 3 )+( 37 )=( 11 )+( 29 )
3
60
3
37
11
29
4. 一个三位数47□,要使它是3的倍数,□里可以填的数有( 1,4,7 );要使它既是3的倍数,又是2的倍数,□里可以填的数有( 4 )。
5. 已知a=2×2×3×5,b=2×5×7,则a和b的最大公因数是( 10 ),最小公倍数是( 420 )。
1,4,
7
4
10
420
6. 从5、2、1、0中选3个数字组成一个同时能被2、3、5整除的最小三位数,并把它分解质因数是( 120=2×2×2×3×5 )。
7. 校运会的开幕式上,五(1)班有男生24人和女生18人参加展演。如果男生和女生要分别排成整行,且每行的人数要相同,每行最多有( 6 )人,一共可以分成( 7 )行。
120=2×2×2×3×5
6
7
二、选择题。
1. 一个长方形的长是奇数,宽是偶数,它的周长一定是( B )。
A. 偶数和质数 B. 偶数和合数
C. 奇数和质数 D. 奇数和合数
2. 下列说法正确的是( D )。
A. 所有的质数都是奇数
B. 两个奇数的差一定是奇数
C. 整数都比分数大
D. 是4的倍数的数一定是偶数
B
D
3. 已知a,b均是大于1的自然数,且a是b的倍数,则下面的说法,错误的是( C )。
A. b是a的因数
B. a是a与b的公倍数
C. a与b的和一定是偶数
D. a与b的积一定不是质数
4. 甲、乙两数的最大公因数是1,最小公倍数是( A )。
A. 甲×乙 B. 甲+乙
C. 甲 D. 乙
C
A
三、解决问题。
1. 某电商平台,一袋大米a元(a为整数),妈妈购了3袋,付钱时妈妈输入265元,小明马上说不对,你觉得对吗?为什么?请说明理由。
妈妈输的不对。
因为妈妈购了3袋大米,所以付的钱数应是3的倍数,265不是3的倍数,所以不对。
2. 张伯伯家厨房长30分米,宽18分米。如果用边长是整分米数的正方形地砖把厨房的地面铺满(使用的地砖要求是整块),地砖的边长最大是几分米?这时需要多少块地砖?
30=2×3×5 18=2×3×3
30和18的最大公因数是∶2×3=6
即正方形地砖的边长最大是6分米。
需要地砖∶30×18÷(6×6)=15(块)
四、 李阿姨到商场买同品牌的桔子饮料,大瓶每瓶6元,小瓶每瓶4元。李阿姨带的钱如果都买小瓶,还剩2元,如果都买大瓶,也剩2元。李阿姨至少带了多少钱?
4=2×2 6=2×3
4和6的最小公倍数是2×2×3=12
至少带了∶12+2=14(元)
