人教版六年级下册数学分数、百分数解决问题课件(共42张PPT)
文档属性
| 名称 | 人教版六年级下册数学分数、百分数解决问题课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
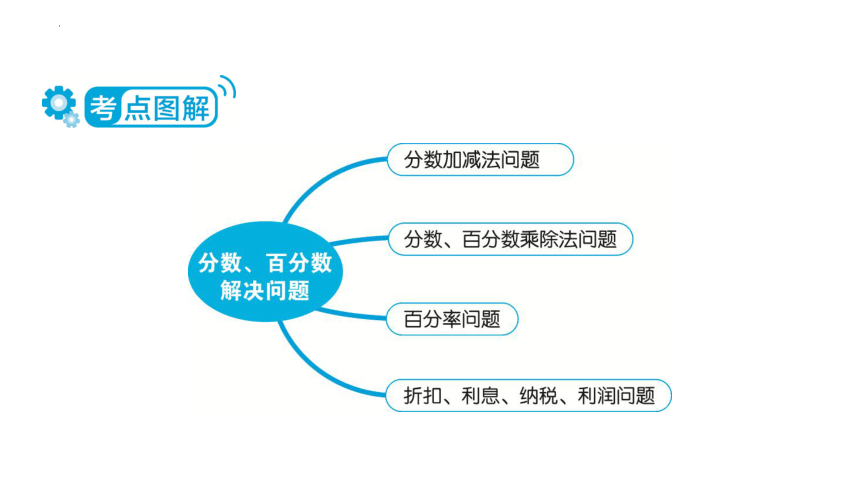
分数、百分数解决问题
考点1 分数加减法问题
考点精讲
分数加减法的应用题与整数加减法的应用题的结构、数量关系和解题方法基本相同,所不同的只是在已知数或未知数中含有分数。
真题精讲
例(金华市永康市)一根长2米的木条,截去米,还剩下( )米。
【解析】用这根木条的长度减去截去的长度,可以计算出还剩的长度为2-=1(米)。
【答案】1
跟踪训练
1. (延安市富县)一根绳子,第一次剪去了 m,第二次剪去了 m,第二次比第一次少剪了( B )m。
A. B. C.
B
2. (吕梁市汾阳市)一根电线长3米,如果用去,还剩全长的( );如果用去米,还剩( 2 )米。
2
考点2 分数、百分数乘除法问题
考点精讲
1. 简单的分数、百分数乘除问题
(1)求一个数是另一个数的几分之几(百分之几),用除法计算。
(2)求一个数的几分之几(百分之几)是多少,用乘法计算。
(3)已知一个数的几分之几(百分之几)是多少,求这个数,用除法计算。
数量关系式∶
(1)标准量(单位“1”的量)×分率(百分率)=比较量(部分量)
(2)比较量(部分量)÷标准量(单位“1”的量)=分率(百分率)
(3)比较量(部分量)÷分率(百分率)=标准量(单位“1”的量)
2. 复杂的分数、百分数乘除问题
(1)求甲数比乙数多或少几分之几(百分之几),用除法计算。
(2)求比一个数多或少几分之几(百分之几)的数是多少,用乘法计算。
(3)已知比一个数多或少几分之几(百分之几)的数是多少,求这个数,用除法计算。
3. 工程问题
把工作总量看作单位“1”,工作效率就是工作时间的倒数,然后根据题目的具体情况,灵活运用公式。
数量关系式∶
工作总量=工作效率×工作时间
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
真题精讲
例1(潮州市)一堆煤,已经运走360吨,是剩下的,这堆煤原来一共有多少吨?
【解析】把剩下的吨数看作单位“1”,根据分数除法的意义,用运走的吨数(360吨)除以,就是剩下的吨数,运走的吨数加剩下的吨数就是原来的吨数。
【答案】360+360÷=900(吨)
答∶这堆煤原来一共有900吨。
例2(江门市台山市)第十届车展中,第一天成交量为100辆,第二天的成交量比第一天增加了,第二天的成交量是多少?
【解析】把第一天的成交量看作单位“1”,第二天成交量比第一天增加了,也就是第二天成交量是第一天成交量的(1+),根据一个数乘分数的意义,用乘法解答。
【答案】100×(1+)=125(辆)
答∶第二天成交量是125辆。
例3(河源市紫金县)一个工厂采用新工艺后,每件产品的成本是49.5元,比原来降低了10%,原来每件产品的成本是多少元?
【解析】根据题意,把原来的成本看作单位“1”,得关系式∶现在的成本=原来的成本×(1-10%),求单位“1”,用除法计算,代入数据计算即可。
【答案】49.5÷(1-10%)=55(元)
答∶原来每件产品的成本是55元。
例4(石家庄鹿泉区)一批零件,师傅单独做需要10小时,徒弟单独做需要15小时。现在师傅先做4小时,再师徒两人合作,还需要几小时才能完成任务?
【解析】把加工这批零件的总数看作单位“1”,先计算出师傅4小时完成的工作量,再计算出剩余的工作量,最后利用工作时间=工作总量÷两人的工作效率和,计算出还需要几小时才能完成任务。
【答案】(1-×4)÷(+)=(小时)
答∶还需要小时才能完成任务。
跟踪训练
1. 某水泥厂计划生产水泥1200吨,实际生产了2000吨,超产了百分之几?(百分号前保留一位小数)
(2000-1200)÷1200≈66.7%
2. (佛山市南海区)生命在于运动。为了进一步提高全体同学的身体素质,拥有健康强壮的体魄,东华小学开展了“天天晨跑”活动。陈刚共跑了60 km,张华所跑路程比陈刚所跑路程的还多8 km。张华共跑了多少 千米?
60×+8=56(km)
3. (河源市紫金县)工程队要修一条长5000米的公路,第一天修了全长的,第二天比第一天多修了,第二天修了多少米?
5000××(1+)=2500(米)
4. (郴州市宜章县)一条水渠长3.3 km,甲工程队单独修要5天修完,乙工程队单独修要6天修完。现两队合修,几天可以完成这条水渠的一半?
÷=(天)
考点3 百分率问题
考点精讲
常见的百分率∶
(1)发芽率=发芽种子数÷试验种子数×100%
(2)小麦的出粉率=面粉的质量÷小麦的质量×100%
(3)产品的合格率=合格的产品数÷产品总数×100%
(4)职工的出勤率=实际出勤人数÷应出勤人数×100%
(5)溶液的浓度=溶质质量÷溶液质量×100%
真题精讲
例1(深圳市龙岗区)在含盐率为20%的盐水中,再加入5克盐和15克水,混合后得到的盐水的含盐率( )。
A. 小于20% B. 等于20%
C. 大于20% D. 以上答案都不对
【解析】5克盐和15克水,则加入的盐水共重(5+15)克,根据“含盐率=盐的质量÷盐水的质量×100%”,求出加入盐水的含盐率是5÷(5+15)×100%=25%,即加入的盐水含盐率比原来盐水的含盐率高,则混合后得到的盐水的含盐率一定比原来含盐率高。
【答案】C
例2(东莞市)一批种子,发芽粒数与没有发芽粒数的比是4∶1,这批种子的发芽率是( )。
A. 80% B. 75% C. 25% D. 20%
【解析】设发芽种子数为“4”,则没有发芽的种子数为“1”,这批种子的总数为“(4+1)”,根据“发芽率=发芽种子数÷试验种子总数×100%”即可解答。
【答案】A
跟踪训练
1. (衡阳市衡山县)王师傅做了101个零件,全部合格,合格率是101%。( × )(判断对错)
2. 用400粒玉米种子做发芽试验,有12粒没有发芽,发芽率是( 97% )。
×
97%
星期 一 二 三 四 五
出勤人数 38 40 37 39 39
星期二的出勤率是100%,哪一天的缺勤率最高,是多少?
40-37=3(人)
3÷40×100%=7.5%
答∶星期三的缺勤率最高,是7.5%。
3. 六(1)班9月份第二周出勤情况如下表∶
4. (揭阳市揭东区)84消毒液是一种高效消毒剂,需要通过稀释才能使用,学校总务处准备配比84消毒液进行消毒。现在有20毫升84消毒原液,要兑成浓度为1%的消毒液需要加入多少升水?
20÷1%-20=1980(毫升)
1980毫升=1.98升
考点4 折扣、利息、纳税、利润问题
考点精讲
1. 折扣问题
(1)商店有时降价出售商品,通常我们把它称为“打折”出售,几折就是百分之几十,几几折就是百分之几十几。
(2)基本数量关系式∶原价×折扣=现价,现价÷折扣=原价,现价÷原价=折扣。
2. 利息问题
(1)利息与本金的比率叫做利率。利率一般有年利率和月利率两种。年利率是指存期一年利息占本金的百分比;月利率是指存期一个月利息占本金的百分比。
(2)基本数量关系式∶利息=本金×利率×存期。
3. 纳税问题
(1)税率∶应纳税额与各种收入的比率叫做税率。
(2)基本数量关系式∶应纳税额=(总收入-免税部分)×税率,总收入=应纳税额÷税率+免税部分。
4. 利润问题
(1)定价与成本之间的差额叫做利润。利润与成本的比率叫做利润率。
(2)基本数量关系式∶利润=定价-成本,利润率=(定价-成本)÷成本×100%。
真题精讲
例1(广州市荔湾区)“六一”儿童节前夕,某品牌的玩具搞促销活动。在A商场打六折出售,在B商场按“每满100元减40元”的方式销售。妈妈要买一个标价240元的这种品牌的玩具。
(1)在A,B两个商场买各应付多少钱?
(2)选择哪个商场更省钱?
【解析】(1)A商场∶用标价乘折扣即可求出实际的价格;B商场∶240元里面有2个100元,可以减去80元,用标价减去优惠掉的80元即为实际的价格。
(2)将两家商场需要的钱数比较即可。
【答案】(1)A商场∶六折=60% 240×60%=144(元)
B商场∶240÷100=2(个)……40(元) 240-40×2=160(元)
答∶在A、B两个商场买各应付144元和160元。
(2)144<160
答∶A商场更省钱。
【解析】1300元里的800元免税,500元按照20%征收个人所得税,据此解答即可。
【答案】(1300-800)×20%=100(元)
答∶爸爸的这笔评审费要缴纳100元个人所得税。
例2(东莞市)爸爸收到一笔专家评审费1300元,按照规定,其中的800元是免税的,超过部分按照20%征收个人所得税,爸爸的这笔评审费要缴纳多少元个人所得税?
跟踪训练
1. 张叔叔的劳务收入是1.5万元,按规定需缴纳20%的个人所得税,张叔叔实际得到了( 12000 )元。
2. (佛山市禅城区)一组沙发按成本加价四成定价,然后打八折销售,能够获利900元,这组沙发的成本是( 7500 )元。
3. (广州市荔湾区)黄叔叔存入银行50000元,定期两年,年利率是2.1%,到期可得到利息( 2100 )元。
12000
7500
2100
4. (渭南市潼关县)受疫情的影响,某商场为了回笼资金,所有商品打七八折出售,已知该商场内一台冰箱打折后的价格比原价便宜了176元,这台冰箱打折后的价格是多少元?
176÷(1-78%)=800(元)
800-176=624(元)
一、填空题。
1. (宁波市海曙区)两根绳子都是4米长,第一根剪去了全长的,还剩全长的( );第二根剪去米,还剩( )米。
2. 比米多米的是( )米;吨比( )吨重吨。
3. (肇庆市广宁县)一项工作一个人单独做完,甲要4天,乙要5天。如果甲、乙合做,需要( )天完成。
4. (昭阳市昭阳县)一台拖拉机小时耕地公顷,照这样计算,耕一公顷地要( )小时,一小时可以耕地( )公顷。
5. (惠州市惠阳区)六(1)班今天有49人到校,1人请假,六(1)班今天出勤率是( 98 )%。
6. 一个空桶装满需要5碗水或8杯水,现将3碗水和2杯水倒入空桶中,水面上升到空桶的( )。
7. (惠州市惠阳区)小刚把得到的4000元压岁钱存入银行,定期2年,如果按年利率4.25%计算,到期后小刚应得的利息是( 340 )元。
8. (揭阳市揭东区)有500克含盐率为4%的盐水,加热一段时间后蒸发了一部分水,测得含盐率为5%,蒸发了( 100 )克水。
98
340
100
二、选择题。
1. 今年的产量比去年多,今年的产量相当于去年的( C )。
A. B. C. D.
2. (佛山市顺德区)一本故事书有140页,奇思已经看了这本书的,还剩( B )页没有看。
A. 80 B. 60 C. 20 D. 100
C
B
3. (信阳市平桥区)一张彩纸,先用去它的,再用去它的,应选择( A )作为测量单位,就能正好测量出共用去几个这样的单位。
A. 彩纸的 B. 彩纸的
C. 彩纸的 D. 彩纸的
A
4. (深圳市龙岗区)乐乐爸爸每月工资7800元,按照《个人所得税法》规定,5000元以内不用交税,每月收入超过5000元的部分按照3%交税,乐乐爸爸每月应交税多少元?下面的算式正确的是( A )。
A. (7800-5000)×3%
B. 7800×3%
C. 5000×3%
D. (7800-5000)×(1-3%)
A
5. (潮州市湘桥区)一段山路,甲需10分钟才能走完,乙需12分钟才能走完,甲的速度比乙的速度( C )。
A. 快 B. 慢
C. 快20% D. 慢20%
C
三、解决问题。
1. 一本故事书240页,黄菲第一天看了40页,第二天看了全书的,两天一共看了这本书的几分之几?
40÷240+=
2. 甲、乙两地相距360千米,一列货车和一列客车从甲、乙两地同时相对开出,已知客车的速度是每小时50千米,货车的速度是客车的,两车开出后几小时相遇?
360÷(50×+50)=4(小时)
3. (广州市荔湾区)4月23日是世界读书日,某书店的图书打七折出售。李红当天到书店买了一套书,比原价节省了28.8元。这套书原价多少钱?
28.8÷(1-70%)=96(元)
4. (揭阳市普宁市)王叔叔要出差,他购买了一张1月8日晚上8∶00开车的火车票,票价300元。由于出差任务取消,他在1月8日早上7∶00到火车站退票。按照规定,火车票退票需要扣除退票手续费(如表)。王叔叔退票后可以拿回多少元?
退票时间 开车前48小时以上 开车前24至48小时 开车前24小时以内
退票手续费占票价的百分比 5% 10% 20%
晚上8∶00即20∶00
20时-7时=13小时
13小时<24小时
300×(1-20%)=240(元)
5. (渭南市韩城市)甲、乙两个工程队合作修一段公路,甲队修了全长的后,乙队接着修了15千米,这时正好修了这段公路的一半。这段公路长多少千米?
15÷=50(千米)
四、仓库里有一批面粉,运出总数的37.5%后,又运进260袋,这时仓库里的面粉恰好是原有面粉的。仓库里原有面粉多少袋?
260÷[-(1-37.5%)]=1120(袋)
分数、百分数解决问题
考点1 分数加减法问题
考点精讲
分数加减法的应用题与整数加减法的应用题的结构、数量关系和解题方法基本相同,所不同的只是在已知数或未知数中含有分数。
真题精讲
例(金华市永康市)一根长2米的木条,截去米,还剩下( )米。
【解析】用这根木条的长度减去截去的长度,可以计算出还剩的长度为2-=1(米)。
【答案】1
跟踪训练
1. (延安市富县)一根绳子,第一次剪去了 m,第二次剪去了 m,第二次比第一次少剪了( B )m。
A. B. C.
B
2. (吕梁市汾阳市)一根电线长3米,如果用去,还剩全长的( );如果用去米,还剩( 2 )米。
2
考点2 分数、百分数乘除法问题
考点精讲
1. 简单的分数、百分数乘除问题
(1)求一个数是另一个数的几分之几(百分之几),用除法计算。
(2)求一个数的几分之几(百分之几)是多少,用乘法计算。
(3)已知一个数的几分之几(百分之几)是多少,求这个数,用除法计算。
数量关系式∶
(1)标准量(单位“1”的量)×分率(百分率)=比较量(部分量)
(2)比较量(部分量)÷标准量(单位“1”的量)=分率(百分率)
(3)比较量(部分量)÷分率(百分率)=标准量(单位“1”的量)
2. 复杂的分数、百分数乘除问题
(1)求甲数比乙数多或少几分之几(百分之几),用除法计算。
(2)求比一个数多或少几分之几(百分之几)的数是多少,用乘法计算。
(3)已知比一个数多或少几分之几(百分之几)的数是多少,求这个数,用除法计算。
3. 工程问题
把工作总量看作单位“1”,工作效率就是工作时间的倒数,然后根据题目的具体情况,灵活运用公式。
数量关系式∶
工作总量=工作效率×工作时间
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
真题精讲
例1(潮州市)一堆煤,已经运走360吨,是剩下的,这堆煤原来一共有多少吨?
【解析】把剩下的吨数看作单位“1”,根据分数除法的意义,用运走的吨数(360吨)除以,就是剩下的吨数,运走的吨数加剩下的吨数就是原来的吨数。
【答案】360+360÷=900(吨)
答∶这堆煤原来一共有900吨。
例2(江门市台山市)第十届车展中,第一天成交量为100辆,第二天的成交量比第一天增加了,第二天的成交量是多少?
【解析】把第一天的成交量看作单位“1”,第二天成交量比第一天增加了,也就是第二天成交量是第一天成交量的(1+),根据一个数乘分数的意义,用乘法解答。
【答案】100×(1+)=125(辆)
答∶第二天成交量是125辆。
例3(河源市紫金县)一个工厂采用新工艺后,每件产品的成本是49.5元,比原来降低了10%,原来每件产品的成本是多少元?
【解析】根据题意,把原来的成本看作单位“1”,得关系式∶现在的成本=原来的成本×(1-10%),求单位“1”,用除法计算,代入数据计算即可。
【答案】49.5÷(1-10%)=55(元)
答∶原来每件产品的成本是55元。
例4(石家庄鹿泉区)一批零件,师傅单独做需要10小时,徒弟单独做需要15小时。现在师傅先做4小时,再师徒两人合作,还需要几小时才能完成任务?
【解析】把加工这批零件的总数看作单位“1”,先计算出师傅4小时完成的工作量,再计算出剩余的工作量,最后利用工作时间=工作总量÷两人的工作效率和,计算出还需要几小时才能完成任务。
【答案】(1-×4)÷(+)=(小时)
答∶还需要小时才能完成任务。
跟踪训练
1. 某水泥厂计划生产水泥1200吨,实际生产了2000吨,超产了百分之几?(百分号前保留一位小数)
(2000-1200)÷1200≈66.7%
2. (佛山市南海区)生命在于运动。为了进一步提高全体同学的身体素质,拥有健康强壮的体魄,东华小学开展了“天天晨跑”活动。陈刚共跑了60 km,张华所跑路程比陈刚所跑路程的还多8 km。张华共跑了多少 千米?
60×+8=56(km)
3. (河源市紫金县)工程队要修一条长5000米的公路,第一天修了全长的,第二天比第一天多修了,第二天修了多少米?
5000××(1+)=2500(米)
4. (郴州市宜章县)一条水渠长3.3 km,甲工程队单独修要5天修完,乙工程队单独修要6天修完。现两队合修,几天可以完成这条水渠的一半?
÷=(天)
考点3 百分率问题
考点精讲
常见的百分率∶
(1)发芽率=发芽种子数÷试验种子数×100%
(2)小麦的出粉率=面粉的质量÷小麦的质量×100%
(3)产品的合格率=合格的产品数÷产品总数×100%
(4)职工的出勤率=实际出勤人数÷应出勤人数×100%
(5)溶液的浓度=溶质质量÷溶液质量×100%
真题精讲
例1(深圳市龙岗区)在含盐率为20%的盐水中,再加入5克盐和15克水,混合后得到的盐水的含盐率( )。
A. 小于20% B. 等于20%
C. 大于20% D. 以上答案都不对
【解析】5克盐和15克水,则加入的盐水共重(5+15)克,根据“含盐率=盐的质量÷盐水的质量×100%”,求出加入盐水的含盐率是5÷(5+15)×100%=25%,即加入的盐水含盐率比原来盐水的含盐率高,则混合后得到的盐水的含盐率一定比原来含盐率高。
【答案】C
例2(东莞市)一批种子,发芽粒数与没有发芽粒数的比是4∶1,这批种子的发芽率是( )。
A. 80% B. 75% C. 25% D. 20%
【解析】设发芽种子数为“4”,则没有发芽的种子数为“1”,这批种子的总数为“(4+1)”,根据“发芽率=发芽种子数÷试验种子总数×100%”即可解答。
【答案】A
跟踪训练
1. (衡阳市衡山县)王师傅做了101个零件,全部合格,合格率是101%。( × )(判断对错)
2. 用400粒玉米种子做发芽试验,有12粒没有发芽,发芽率是( 97% )。
×
97%
星期 一 二 三 四 五
出勤人数 38 40 37 39 39
星期二的出勤率是100%,哪一天的缺勤率最高,是多少?
40-37=3(人)
3÷40×100%=7.5%
答∶星期三的缺勤率最高,是7.5%。
3. 六(1)班9月份第二周出勤情况如下表∶
4. (揭阳市揭东区)84消毒液是一种高效消毒剂,需要通过稀释才能使用,学校总务处准备配比84消毒液进行消毒。现在有20毫升84消毒原液,要兑成浓度为1%的消毒液需要加入多少升水?
20÷1%-20=1980(毫升)
1980毫升=1.98升
考点4 折扣、利息、纳税、利润问题
考点精讲
1. 折扣问题
(1)商店有时降价出售商品,通常我们把它称为“打折”出售,几折就是百分之几十,几几折就是百分之几十几。
(2)基本数量关系式∶原价×折扣=现价,现价÷折扣=原价,现价÷原价=折扣。
2. 利息问题
(1)利息与本金的比率叫做利率。利率一般有年利率和月利率两种。年利率是指存期一年利息占本金的百分比;月利率是指存期一个月利息占本金的百分比。
(2)基本数量关系式∶利息=本金×利率×存期。
3. 纳税问题
(1)税率∶应纳税额与各种收入的比率叫做税率。
(2)基本数量关系式∶应纳税额=(总收入-免税部分)×税率,总收入=应纳税额÷税率+免税部分。
4. 利润问题
(1)定价与成本之间的差额叫做利润。利润与成本的比率叫做利润率。
(2)基本数量关系式∶利润=定价-成本,利润率=(定价-成本)÷成本×100%。
真题精讲
例1(广州市荔湾区)“六一”儿童节前夕,某品牌的玩具搞促销活动。在A商场打六折出售,在B商场按“每满100元减40元”的方式销售。妈妈要买一个标价240元的这种品牌的玩具。
(1)在A,B两个商场买各应付多少钱?
(2)选择哪个商场更省钱?
【解析】(1)A商场∶用标价乘折扣即可求出实际的价格;B商场∶240元里面有2个100元,可以减去80元,用标价减去优惠掉的80元即为实际的价格。
(2)将两家商场需要的钱数比较即可。
【答案】(1)A商场∶六折=60% 240×60%=144(元)
B商场∶240÷100=2(个)……40(元) 240-40×2=160(元)
答∶在A、B两个商场买各应付144元和160元。
(2)144<160
答∶A商场更省钱。
【解析】1300元里的800元免税,500元按照20%征收个人所得税,据此解答即可。
【答案】(1300-800)×20%=100(元)
答∶爸爸的这笔评审费要缴纳100元个人所得税。
例2(东莞市)爸爸收到一笔专家评审费1300元,按照规定,其中的800元是免税的,超过部分按照20%征收个人所得税,爸爸的这笔评审费要缴纳多少元个人所得税?
跟踪训练
1. 张叔叔的劳务收入是1.5万元,按规定需缴纳20%的个人所得税,张叔叔实际得到了( 12000 )元。
2. (佛山市禅城区)一组沙发按成本加价四成定价,然后打八折销售,能够获利900元,这组沙发的成本是( 7500 )元。
3. (广州市荔湾区)黄叔叔存入银行50000元,定期两年,年利率是2.1%,到期可得到利息( 2100 )元。
12000
7500
2100
4. (渭南市潼关县)受疫情的影响,某商场为了回笼资金,所有商品打七八折出售,已知该商场内一台冰箱打折后的价格比原价便宜了176元,这台冰箱打折后的价格是多少元?
176÷(1-78%)=800(元)
800-176=624(元)
一、填空题。
1. (宁波市海曙区)两根绳子都是4米长,第一根剪去了全长的,还剩全长的( );第二根剪去米,还剩( )米。
2. 比米多米的是( )米;吨比( )吨重吨。
3. (肇庆市广宁县)一项工作一个人单独做完,甲要4天,乙要5天。如果甲、乙合做,需要( )天完成。
4. (昭阳市昭阳县)一台拖拉机小时耕地公顷,照这样计算,耕一公顷地要( )小时,一小时可以耕地( )公顷。
5. (惠州市惠阳区)六(1)班今天有49人到校,1人请假,六(1)班今天出勤率是( 98 )%。
6. 一个空桶装满需要5碗水或8杯水,现将3碗水和2杯水倒入空桶中,水面上升到空桶的( )。
7. (惠州市惠阳区)小刚把得到的4000元压岁钱存入银行,定期2年,如果按年利率4.25%计算,到期后小刚应得的利息是( 340 )元。
8. (揭阳市揭东区)有500克含盐率为4%的盐水,加热一段时间后蒸发了一部分水,测得含盐率为5%,蒸发了( 100 )克水。
98
340
100
二、选择题。
1. 今年的产量比去年多,今年的产量相当于去年的( C )。
A. B. C. D.
2. (佛山市顺德区)一本故事书有140页,奇思已经看了这本书的,还剩( B )页没有看。
A. 80 B. 60 C. 20 D. 100
C
B
3. (信阳市平桥区)一张彩纸,先用去它的,再用去它的,应选择( A )作为测量单位,就能正好测量出共用去几个这样的单位。
A. 彩纸的 B. 彩纸的
C. 彩纸的 D. 彩纸的
A
4. (深圳市龙岗区)乐乐爸爸每月工资7800元,按照《个人所得税法》规定,5000元以内不用交税,每月收入超过5000元的部分按照3%交税,乐乐爸爸每月应交税多少元?下面的算式正确的是( A )。
A. (7800-5000)×3%
B. 7800×3%
C. 5000×3%
D. (7800-5000)×(1-3%)
A
5. (潮州市湘桥区)一段山路,甲需10分钟才能走完,乙需12分钟才能走完,甲的速度比乙的速度( C )。
A. 快 B. 慢
C. 快20% D. 慢20%
C
三、解决问题。
1. 一本故事书240页,黄菲第一天看了40页,第二天看了全书的,两天一共看了这本书的几分之几?
40÷240+=
2. 甲、乙两地相距360千米,一列货车和一列客车从甲、乙两地同时相对开出,已知客车的速度是每小时50千米,货车的速度是客车的,两车开出后几小时相遇?
360÷(50×+50)=4(小时)
3. (广州市荔湾区)4月23日是世界读书日,某书店的图书打七折出售。李红当天到书店买了一套书,比原价节省了28.8元。这套书原价多少钱?
28.8÷(1-70%)=96(元)
4. (揭阳市普宁市)王叔叔要出差,他购买了一张1月8日晚上8∶00开车的火车票,票价300元。由于出差任务取消,他在1月8日早上7∶00到火车站退票。按照规定,火车票退票需要扣除退票手续费(如表)。王叔叔退票后可以拿回多少元?
退票时间 开车前48小时以上 开车前24至48小时 开车前24小时以内
退票手续费占票价的百分比 5% 10% 20%
晚上8∶00即20∶00
20时-7时=13小时
13小时<24小时
300×(1-20%)=240(元)
5. (渭南市韩城市)甲、乙两个工程队合作修一段公路,甲队修了全长的后,乙队接着修了15千米,这时正好修了这段公路的一半。这段公路长多少千米?
15÷=50(千米)
四、仓库里有一批面粉,运出总数的37.5%后,又运进260袋,这时仓库里的面粉恰好是原有面粉的。仓库里原有面粉多少袋?
260÷[-(1-37.5%)]=1120(袋)
