人教版小学数学六年级下册《四则混合运算和简便运算》课件(共33张PPT)
文档属性
| 名称 | 人教版小学数学六年级下册《四则混合运算和简便运算》课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 00:00:00 | ||
图片预览




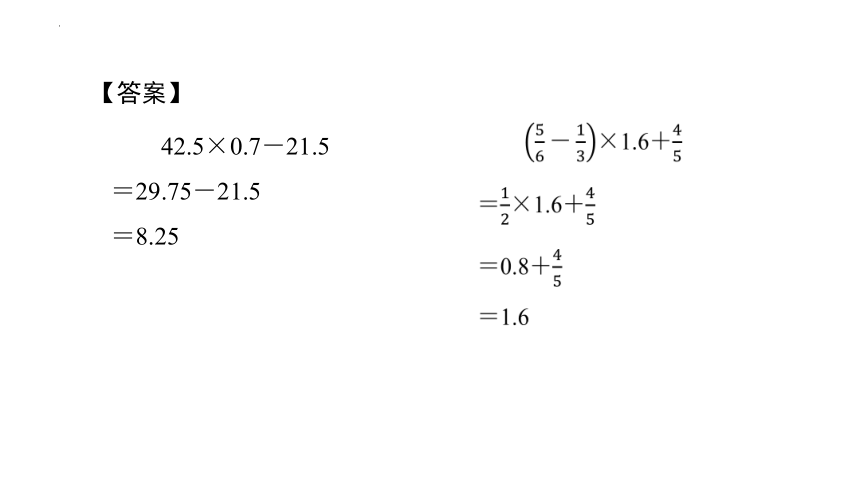
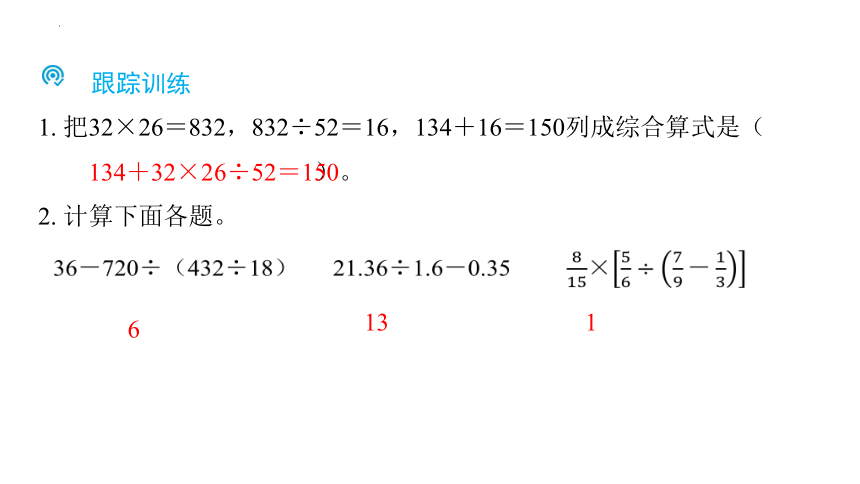





文档简介
(共33张PPT)
四则混合运算和简便运算
考点1 四则混合运算
考点精讲
1. 四则混合运算的顺序
加、减法叫做一级运算,乘、除法叫做二级运算。在没有括号的算式里,先算二级运算,再算一级运算;同级运算,从左往右依次计算;如果有括号,先算括号里面的。
2. 注意事项
在四则混合运算中,要先确定好运算顺序,再计算。计算时,不一定把全题统一化成分数或化成小数计算,可以根据运算顺序,分成几部分进行处理,选择合适的算法。
真题精讲
例(广州市)计算下面各题。
42.5×0.7-21.5 ×1.6+
【解析】(1)根据运算顺序,先计算乘法,再计算减法;
(2)根据运算顺序,先计算括号里的减法,再计算括号外的乘法,最后计算括号外的加法。
42.5×0.7-21.5
=29.75-21.5
=8.25
【答案】
×1.6+
=×1.6+
=0.8+
=1.6
跟踪训练
1. 把32×26=832,832÷52=16,134+16=150列成综合算式是( 134+32×26÷52=150 )。
2. 计算下面各题。
36-720÷(432÷18) 21.36÷1.6-0.35 ×
6
13
1
134+32×26÷52=150
考点2 运算定律和运算性质
考点精讲
1. 运算定律
(1)加法运算定律
加法交换律∶a+b=b+a
加法结合律∶(a+b)+c=a+(b+c)
(2)乘法运算定律
乘法交换律∶a×b=b×a
乘法结合律∶(a×b)×c=a×(b×c)
乘法分配律∶(a+b)×c=a×c+b×c
乘法分配律扩展∶(a-b)×c=a×c-b×c
2. 运算性质
(1)减法运算性质
a-b-c=a-(b+c) a-b-c=a-c-b
(2)除法运算性质
a÷b÷c=a÷(b×c) a÷b÷c=a÷c÷b
(3)其他运算性质
a-b+c=a+c-b a-b+c=a-(b-c)
a÷b×c=a×c÷b a÷b×c=a÷(b÷c)
真题精讲
例1(江门市台山市)下面各式中,运用了加法结合律的是( )。
A. 2.3+1.9=1.9+2.3
B. 4.6-1.8-0.2=4.6-(1.8+0.2)
C. 0.7+1.6+1.4=0.7+(1.6+1.4)
【解析】加法结合律用字母表示为∶a+b+c=a+(b+c),据此选择即可。
【答案】C
例2(广州市增城区)下面每个选项都有两道算式,不能用等号连接的一组算式是( )。
A. ×99和×100- B. ×和×
C. --和- D. ×和××
【解析】A. 把99拆成100-1,再利用乘法分配律,则有×99=×=×100-
B. 利用乘法结合律,则有×=×
C. 利用减法的性质,则有--=-
D. ×和××结果不相等
【答案】D
跟踪训练
1. (珠海市金湾区)用计算器计算“23×59”时,发现计算器按键“9”坏了,小明说∶“我可以用23×60-23来解决。”如果你还用这个计算器,你还会怎样计算?请写出算式∶( 23×61-23×2 )。
2. 在计算44×25时,两位同学用了不同的方法进行简便计算(如图)。甲运用了乘法( 结合 )律,乙运用了乘法( 分配 )律。
甲∶44×25=11×(4×25) 乙∶44×25=40×25+4×25
23×61-23×2
结合
分配
考点3 简便计算
考点精讲
1. 简便计算的常见方法
(1)结合算式的特点,利用四则运算定律和性质进行简便计算。
(2)拆分法∶当一个数比整百、整千稍微大一些的时候,我们可以把这个数拆分成整百、整千与一个较小数的和,然后利用加减法的交换、结合律进行简便计算。
例如∶103=100+3,1006=1000+6。
(3)凑整法∶当一个数比整百、整千稍微小一些的时候,我们可以把这个数写成一个整百、整千的数减去一个较小数的形式,然后利用加减法的运算定律进行简便计算。例如∶97=100-3, 998=1000-2。
2. 简便计算的技巧
(1)同种运算想交换律和结合律;交换就是为了结合。
(2)有乘有加(或有减)有相同数,要想乘法分配律,无相同数找倍数关系变相同数用乘法分配律(即两个乘法算式相加或相减,就可以用乘法分配律)。
(3)加减混合运算,看清数字特点,用好减法的性质。
(4)乘除混合运算用好除法的性质(即乘除法添、去括号规则)。
(5)牢记见25想4,见125想8,见5想2等积能凑整的特殊数字,用好商不变规律。
真题精讲
例(广州市荔湾区)简便计算。
137.4-8.47-1.53 0.25×64×1.25 ×+÷9
【解析】第一题利用减法的性质进行简算;第二题将64拆分成8×8,再利用乘法结合律进行简算;第三题将算式转化为×+×,再利用乘法分配律进行简算即可。
137.4-8.47-1.53
=137.4-(8.47+1.53)
=137.4-10
=127.4
【答案】
0.25×64×1.25
=0.25×(8×8)×1.25
=(0.25×8)×(8×1.25)
=2×10
=20
×+÷9
=×+×
=×
=
跟踪训练
1. (惠州市博罗县)简便计算。
8.5+1.7-2.5+3.3 ÷+× 4×(+)×5
11
9
2. 简便运算。
9+99+999+1 +++
1110
一、填空题。
1. 根据我们学过的运算定律,在□里填上适当的数。
(7.3×1.25)× 8 =7.3×( 1 . 2 5 ×8)
9×1.9+9×8.1= 9 ×( 1 . 9 + 8 . 1 )
2. 6×4×2.5=6×(4×2.5),运用了乘法( 结合 )律;(40+4)×2.5=40×2.5+4×2.5运用了乘法( 分配 )律。
8
1 . 2 5
9
1 . 9
8 .
1
结合
分配
4. 要使43×☆+☆×57=2400等式成立,☆代表的数等于( 24 )。
5. 如果 a+b=300,且a-b=150,那么 a+(b+40)=( 340 ),a-(b-60)=( 210 )。
24
340
210
3. 已知○-△=10,那么68×○-68×△=( 680 )(最后结果)。
680
二、选择题。
1. 下面和(80+4)×25结果相等的算式是( B )。
A. 80×4×25 B. 80×25+4×25
C. 80+(25×4) D. 80×25+4
2. 计算0.25×32,最简便的方法是( B )。
A. 0.25×16×2
B. 0.25×4×8
C. 0.25×30+0.25×2
D. 0.5×0.5×32
B
B
3. (天津市北辰区)与24÷结果相等的式子是( B )
A. 24÷5×3 B. 24÷3×5
C. 24÷3÷5 D. 24×3×5
B
4. (广州市增城区)下面算式中,不符合乘法分配律的算式是( B )。
A. 117×3+117×7=117×(3+7)
B. 25×(5+12)=25×5+12
C. (5+1)×▲=5×▲+▲
D. a×(b+c)=a×b+a×c
B
5. 下面的计算过程,应用了什么运算定律?( B )
22×19+11×12
=11×(2×19)+11×12
=11×38+11×12
=11×(38+12)
A. 只应用了乘法结合律
B. 同时应用了乘法结合律和分配律
C. 同时应用了乘法交换律、结合律和分配律
D. 同时应用了加法结合律和交换律
B
6. 小明在算0.6×(□+3)时忘记了有小括号,他的计算结果与正确结果相比,( C )。
A. 多了1.8 B. 小了1.8
C. 多了1.2 D. 多了3
C
三、计算题。
1. 直接写出得数。
2.5×4=10 ×= ÷=
-0.25=0 -= 1--=0
1÷20%=5 80%×= 2.5÷×=17
10
0
0
5
17
2. 计算下面各题,能简算的要简算。
-- (+-)×24
19
2÷[(-0.25)×]
222×48+666×84 (+)×8+
66600
4
18-(2.25+8.6)-2
5
0.75×101- 7.4×0.8+2.6×0.8
75
8
[1-(-)]÷ ÷(×-)
÷[×(-)]
12.5×2.5÷×80% +×(1-)
100
75%×+÷ (+)×12×17
53
53×68%+0.32×53
53
四、 怎样简便怎样算。
1880×201.1-187.9×2011
=1880×201.1-1879×201.1
=201.1×(1880-1879)
=201.1×1
=201.1
=×+×+×
=(++)×
=(++)×
=×
=
×+×+×
五、用简便方法计算。
(1+++)×(+++)-(1++++)×(++)
设1+++=a,++=b
原式=a×-×b
=-
=ab+a-ab-b
=
=×
=×
=×1
=
四则混合运算和简便运算
考点1 四则混合运算
考点精讲
1. 四则混合运算的顺序
加、减法叫做一级运算,乘、除法叫做二级运算。在没有括号的算式里,先算二级运算,再算一级运算;同级运算,从左往右依次计算;如果有括号,先算括号里面的。
2. 注意事项
在四则混合运算中,要先确定好运算顺序,再计算。计算时,不一定把全题统一化成分数或化成小数计算,可以根据运算顺序,分成几部分进行处理,选择合适的算法。
真题精讲
例(广州市)计算下面各题。
42.5×0.7-21.5 ×1.6+
【解析】(1)根据运算顺序,先计算乘法,再计算减法;
(2)根据运算顺序,先计算括号里的减法,再计算括号外的乘法,最后计算括号外的加法。
42.5×0.7-21.5
=29.75-21.5
=8.25
【答案】
×1.6+
=×1.6+
=0.8+
=1.6
跟踪训练
1. 把32×26=832,832÷52=16,134+16=150列成综合算式是( 134+32×26÷52=150 )。
2. 计算下面各题。
36-720÷(432÷18) 21.36÷1.6-0.35 ×
6
13
1
134+32×26÷52=150
考点2 运算定律和运算性质
考点精讲
1. 运算定律
(1)加法运算定律
加法交换律∶a+b=b+a
加法结合律∶(a+b)+c=a+(b+c)
(2)乘法运算定律
乘法交换律∶a×b=b×a
乘法结合律∶(a×b)×c=a×(b×c)
乘法分配律∶(a+b)×c=a×c+b×c
乘法分配律扩展∶(a-b)×c=a×c-b×c
2. 运算性质
(1)减法运算性质
a-b-c=a-(b+c) a-b-c=a-c-b
(2)除法运算性质
a÷b÷c=a÷(b×c) a÷b÷c=a÷c÷b
(3)其他运算性质
a-b+c=a+c-b a-b+c=a-(b-c)
a÷b×c=a×c÷b a÷b×c=a÷(b÷c)
真题精讲
例1(江门市台山市)下面各式中,运用了加法结合律的是( )。
A. 2.3+1.9=1.9+2.3
B. 4.6-1.8-0.2=4.6-(1.8+0.2)
C. 0.7+1.6+1.4=0.7+(1.6+1.4)
【解析】加法结合律用字母表示为∶a+b+c=a+(b+c),据此选择即可。
【答案】C
例2(广州市增城区)下面每个选项都有两道算式,不能用等号连接的一组算式是( )。
A. ×99和×100- B. ×和×
C. --和- D. ×和××
【解析】A. 把99拆成100-1,再利用乘法分配律,则有×99=×=×100-
B. 利用乘法结合律,则有×=×
C. 利用减法的性质,则有--=-
D. ×和××结果不相等
【答案】D
跟踪训练
1. (珠海市金湾区)用计算器计算“23×59”时,发现计算器按键“9”坏了,小明说∶“我可以用23×60-23来解决。”如果你还用这个计算器,你还会怎样计算?请写出算式∶( 23×61-23×2 )。
2. 在计算44×25时,两位同学用了不同的方法进行简便计算(如图)。甲运用了乘法( 结合 )律,乙运用了乘法( 分配 )律。
甲∶44×25=11×(4×25) 乙∶44×25=40×25+4×25
23×61-23×2
结合
分配
考点3 简便计算
考点精讲
1. 简便计算的常见方法
(1)结合算式的特点,利用四则运算定律和性质进行简便计算。
(2)拆分法∶当一个数比整百、整千稍微大一些的时候,我们可以把这个数拆分成整百、整千与一个较小数的和,然后利用加减法的交换、结合律进行简便计算。
例如∶103=100+3,1006=1000+6。
(3)凑整法∶当一个数比整百、整千稍微小一些的时候,我们可以把这个数写成一个整百、整千的数减去一个较小数的形式,然后利用加减法的运算定律进行简便计算。例如∶97=100-3, 998=1000-2。
2. 简便计算的技巧
(1)同种运算想交换律和结合律;交换就是为了结合。
(2)有乘有加(或有减)有相同数,要想乘法分配律,无相同数找倍数关系变相同数用乘法分配律(即两个乘法算式相加或相减,就可以用乘法分配律)。
(3)加减混合运算,看清数字特点,用好减法的性质。
(4)乘除混合运算用好除法的性质(即乘除法添、去括号规则)。
(5)牢记见25想4,见125想8,见5想2等积能凑整的特殊数字,用好商不变规律。
真题精讲
例(广州市荔湾区)简便计算。
137.4-8.47-1.53 0.25×64×1.25 ×+÷9
【解析】第一题利用减法的性质进行简算;第二题将64拆分成8×8,再利用乘法结合律进行简算;第三题将算式转化为×+×,再利用乘法分配律进行简算即可。
137.4-8.47-1.53
=137.4-(8.47+1.53)
=137.4-10
=127.4
【答案】
0.25×64×1.25
=0.25×(8×8)×1.25
=(0.25×8)×(8×1.25)
=2×10
=20
×+÷9
=×+×
=×
=
跟踪训练
1. (惠州市博罗县)简便计算。
8.5+1.7-2.5+3.3 ÷+× 4×(+)×5
11
9
2. 简便运算。
9+99+999+1 +++
1110
一、填空题。
1. 根据我们学过的运算定律,在□里填上适当的数。
(7.3×1.25)× 8 =7.3×( 1 . 2 5 ×8)
9×1.9+9×8.1= 9 ×( 1 . 9 + 8 . 1 )
2. 6×4×2.5=6×(4×2.5),运用了乘法( 结合 )律;(40+4)×2.5=40×2.5+4×2.5运用了乘法( 分配 )律。
8
1 . 2 5
9
1 . 9
8 .
1
结合
分配
4. 要使43×☆+☆×57=2400等式成立,☆代表的数等于( 24 )。
5. 如果 a+b=300,且a-b=150,那么 a+(b+40)=( 340 ),a-(b-60)=( 210 )。
24
340
210
3. 已知○-△=10,那么68×○-68×△=( 680 )(最后结果)。
680
二、选择题。
1. 下面和(80+4)×25结果相等的算式是( B )。
A. 80×4×25 B. 80×25+4×25
C. 80+(25×4) D. 80×25+4
2. 计算0.25×32,最简便的方法是( B )。
A. 0.25×16×2
B. 0.25×4×8
C. 0.25×30+0.25×2
D. 0.5×0.5×32
B
B
3. (天津市北辰区)与24÷结果相等的式子是( B )
A. 24÷5×3 B. 24÷3×5
C. 24÷3÷5 D. 24×3×5
B
4. (广州市增城区)下面算式中,不符合乘法分配律的算式是( B )。
A. 117×3+117×7=117×(3+7)
B. 25×(5+12)=25×5+12
C. (5+1)×▲=5×▲+▲
D. a×(b+c)=a×b+a×c
B
5. 下面的计算过程,应用了什么运算定律?( B )
22×19+11×12
=11×(2×19)+11×12
=11×38+11×12
=11×(38+12)
A. 只应用了乘法结合律
B. 同时应用了乘法结合律和分配律
C. 同时应用了乘法交换律、结合律和分配律
D. 同时应用了加法结合律和交换律
B
6. 小明在算0.6×(□+3)时忘记了有小括号,他的计算结果与正确结果相比,( C )。
A. 多了1.8 B. 小了1.8
C. 多了1.2 D. 多了3
C
三、计算题。
1. 直接写出得数。
2.5×4=10 ×= ÷=
-0.25=0 -= 1--=0
1÷20%=5 80%×= 2.5÷×=17
10
0
0
5
17
2. 计算下面各题,能简算的要简算。
-- (+-)×24
19
2÷[(-0.25)×]
222×48+666×84 (+)×8+
66600
4
18-(2.25+8.6)-2
5
0.75×101- 7.4×0.8+2.6×0.8
75
8
[1-(-)]÷ ÷(×-)
÷[×(-)]
12.5×2.5÷×80% +×(1-)
100
75%×+÷ (+)×12×17
53
53×68%+0.32×53
53
四、 怎样简便怎样算。
1880×201.1-187.9×2011
=1880×201.1-1879×201.1
=201.1×(1880-1879)
=201.1×1
=201.1
=×+×+×
=(++)×
=(++)×
=×
=
×+×+×
五、用简便方法计算。
(1+++)×(+++)-(1++++)×(++)
设1+++=a,++=b
原式=a×-×b
=-
=ab+a-ab-b
=
=×
=×
=×1
=
