人教版六年级下册数学 比和比例的应用(课件)(共28张PPT)
文档属性
| 名称 | 人教版六年级下册数学 比和比例的应用(课件)(共28张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 812.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 22:32:01 | ||
图片预览








文档简介
(共28张PPT)
比和比例的应用
考点精讲
1. 用整数乘、除法解决问题
把一个总数按一定的比来分配,把各部分的比看做份数关系,先求出每一份。
2. 用分数乘法解决问题
把各部分的比转化为总数的几分之几,直接求出总数的几分之几是多少。
考点1 比的应用
真题精讲
例(汕头市金平区)一套运动服的价格是144元,裤子和上衣价格的比是7∶9,裤子的价格是多少元?
【解析】把这套运动服的价格看作单位“1”,裤子的价格占这套运动服价格的,根据这套运动服的价格用乘法求出裤子的价格,据此解答。
【答案】144×=63(元)
答∶裤子的价格是63元。
跟踪训练
1. (广州市从化区)文明路小学50位同学参加经典美文诵读比赛,其中男、女生人数比是2∶3,男、女生各有多少人?
阅读与理解∶“男、女生人数比是2∶3”就是说,把50人平均分成( 5 )份,其中男生占( 2 )份,女生占( 3 )份。
分析与解答∶50×=20(人);50×=30(人);
5
2
3
50×=20(人);50×=30(人);
列式计算∶
回顾与反思∶男生有( 20 )人,女生有( 30 )人,男、女生比是( 2∶3 )。
20
30
2∶3
2. (揭阳市惠来县)笑笑按照说明书上1∶4的比调制了一杯100毫升的蜂蜜水给妈妈喝,妈妈尝了一口,说∶“笑笑,你把这杯水的甜味调得再淡些吧,浓度是10%就可以了。”同学们,你能帮笑笑想想办法吗?请通过列式计算说明你的方法。
100×÷10%-100=100(毫升)
需要加水100毫升。
考点2 比例的应用
考点精讲
1. 比例尺的应用
=比例尺 图上距离=比例尺×实际距离
实际距离=图上距离÷比例尺
2. 正、反比例解决问题
(1)审题,找出题中相关联的两个量。
(2)分析,判断题中相关联的两个量是成正比例关系还是成反比例关系。
(3)设未知数,列比例式。
(4)解比例式。
(5)检验,写答语。
真题精讲
例1(佛山市南海区)街心公园要建一个长方形的花坛,长120米,宽80米。请你按1∶2000的比例尺计算出花坛长和宽的图上距离。
【解析】图上距离=实际距离×比例尺
【答案】120米=12000厘米,80米=8000厘米
12000×=6(厘米),8000×=4(厘米)
答∶花坛长和宽的图上距离分别是6厘米和4厘米。
例2(东莞市)六年级办公室买进一些A4纸,如果平均每天用20张,可以用28天,实际每天节约用纸4张,这些A4纸实际可用多少天?(用比例解)
【解析】设这些A4纸实际可用x天,根据平均每天用纸张数×可用天数=总张数(一定),列出反比例算式解答即可。
【答案】解∶设这些A4纸实际可用x天。
(20-4)x=20×28
x=35
答∶这些A4纸实际可用35天。
跟踪训练
1. 北京到济南高速公路距离大约为430 km,北京到天津大约为120 km。一辆汽车从北京出发开往济南,当行驶到天津时用了1.5小时。按照这个速度,北京到济南全程需要多少小时?(用比例解)
解∶设北京到济南全程需要x小时。
120∶1.5=430∶x
120x=430×1.5
x=5.375
2. (中山市)学校装修一个地面为正方形的阅览室,用边长0.5米的正方形地砖铺地,正好需要144块。如果改用边长0.6米的正方形地砖铺地,需要多少块?(用比例解)
解∶设需要x块。
0.5×0.5×144=0.6×0.6×x
x=100
3. 在比例尺是1∶8000000的地图上,量得两地间的距离是6厘米,甲、乙两车同时从两地相对开出,3小时后相遇,甲、乙两车的速度比是3∶5,甲、乙两车每小时分别行驶多少千米?(用比例解)
6÷=48000000(厘米) 48000000厘米=480千米
解∶设甲车每小时行驶3x千米,乙车每小时行驶5x千米。
3x×3+5x×3=480
x=20
甲车∶20×3=60(千米) 乙车∶20×5=100(千米)
一、填空题。
1. 学校长跑队女运动员是男运动员人数的,女运动员人数与总人数的比是( 3∶11 )。
2. (东莞市)一个三角形三个内角度数的比是2∶2∶5。这个三角形按角分类属于( 钝角 )三角形,按边分类属于( 等腰 )三角形。
3. (阳江市江城区)被减数、减数与差的和是100,差与减数的比是1∶4,差是( 10 ),减数是( 40 ),被减数是( 50 )。
3∶11
钝角
等腰
10
40
50
4. (佛山市三水区)小明看一本故事书,已看的页数与未看页数的比是3∶5,未看的有40页,这本书共有( 64 )页,已看( 24 )页。
5. (潮州市湘桥区)如图是一张地图上的比例尺,将它转换为数值比例尺是( 1∶3000000 )。在这张地图上量得两地之间的距离为8.5厘米,则两地之间的实际距离是( 255 )千米。
64
24
1∶3000000
255
6. (大同市新荣区)小张和小杨是同一家快递公司的两名派件员。上周小张和小杨派送快递件数的比是7∶5,小张比小杨多派送了120件快递。上周小张和小杨一共派送了( 720 )件快递。
720
二、选择题。
1. 学校足球场长100米,宽64米,画在校园平面图上,长是5厘米。下面说法正确的是( D )。
A. 这幅图的比例尺是1∶20
B. 这幅图的比例尺是1∶200
C. 宽要画6.4厘米
D. 宽要画3.2厘米
D
2. (深圳市福田区)《庄子·天下篇》中“一尺之棰,日取其半,万世不竭”的意思是∶一尺长的木棒,第一天截取它长度的一半,以后每天都截取它前一天的一半,那么将永远也截取不完。如果按照这种截取方法,那么第3天截取的木棒长度与原来的木棒总长度的比是( D )。
A. 1∶2 B. 1∶3
C. 1∶6 D. 1∶8
D
3. (广州市白云区)六(1)班有学生44人,男生与女生人数的比可能是( D )。
A. 2∶3 B. 3∶4
C. 4∶5 D. 5∶6
4. 在比例尺是1∶3000000的地图上,量得A,B两港距离为12厘米,一艘货轮于上午7时以每小时24千米的速度从A港开向B港,到达B港的时间是( D )。
A. 16时 B. 18时
C. 20时 D. 22时
D
D
5. (广州市增城区)图中表示斑马和长颈鹿的奔跑情况。下面叙述错误的是( C )。
A. 如图是一个正比例关系的图象
B. 在20分钟时,它们路程相差8 km
C. 斑马和长颈鹿的速度之比是2∶3
D. 在15分钟时,长颈鹿跑了12 km
C
三、解决问题。
1. (广州市增城区)小芳练习口算的情况如图,照这样的速度,小芳6分钟能做多少道题?(用比例解)
解∶设小芳6分钟能做x道题。
x∶6=25∶2
2x=6×25
x=75
2. 一间房子要用方砖铺地,用面积是9平方分米的方砖,需用96块,如果改用边长是4分米的方砖,需用多少块?(用比例解)
解∶设需要x块。
4×4x=9×96
x=54
3. (济南市市中区)公园里有一个花坛,面积是100平方米,其中的30%种月季,剩下的面积按3∶4的比分别种玫瑰与牡丹,种玫瑰的面积是多少平方米?
100×(1-30%)×=30(平方米)
4. (韶关市曲江区)客车和货车同时从甲、乙两地的中间向相反的方向行驶,3小时后,客车到达甲地,货车离乙地还有40千米。已知货车和客车的速度比是5∶7,甲、乙两地相距多少千米?
40÷(1-)=140(千米)
140×2=280(千米)
答∶甲、乙两地相距280千米。
四、六年级三个志愿小队的同学收集废纸,第一小队收集的废纸占总数的25%,第二小队收集的废纸质量与第三小队收集的废纸质量的比是7∶8,第一小队比第三小队收集的废纸质量少45千克。三个小队一共收集了废纸多少千克?
解∶设三个小队一共收集了废纸x千克,则第一小队收集的废纸质量是25%x千克,第三小队收集的废纸质量是
(1-25%)x×=×x=x千克,
列方程∶x-25%x=45
x=300
五、(深圳市光明区)在比例尺是1∶5000000的地图上,量得甲地到乙地的图上距离是9厘米。李老师一家上午8∶00驾车从甲地前往乙地,小车平均每小时行驶100千米。
(1)上午11∶00时小车行驶至哪里?请在图中用“ ”标出,并简要说明理由。
11∶00-8∶00=3(小时)
100×3=300(千米)=30000000(厘米)
30000000×=6(厘米)
作图如下∶
(2)小车每行驶100千米消耗汽油8升,出发时油箱里有40升汽油,中途还需要再加油吗?(写出计算过程)
9÷=45000000(厘米)=450(千米)
450÷100×8=36(升)
36升<40升
所以中途不需要再加油。
(3)上午11∶00后,由于路上车流量增加,小车的平均速度下降了10%,那么李老师到达乙地的最早时间是几点几分?
100×(1-10%)=90(千米)
(450-300)÷90=1(小时)
1=1小时40分
11∶00+1小时40分=12∶40
比和比例的应用
考点精讲
1. 用整数乘、除法解决问题
把一个总数按一定的比来分配,把各部分的比看做份数关系,先求出每一份。
2. 用分数乘法解决问题
把各部分的比转化为总数的几分之几,直接求出总数的几分之几是多少。
考点1 比的应用
真题精讲
例(汕头市金平区)一套运动服的价格是144元,裤子和上衣价格的比是7∶9,裤子的价格是多少元?
【解析】把这套运动服的价格看作单位“1”,裤子的价格占这套运动服价格的,根据这套运动服的价格用乘法求出裤子的价格,据此解答。
【答案】144×=63(元)
答∶裤子的价格是63元。
跟踪训练
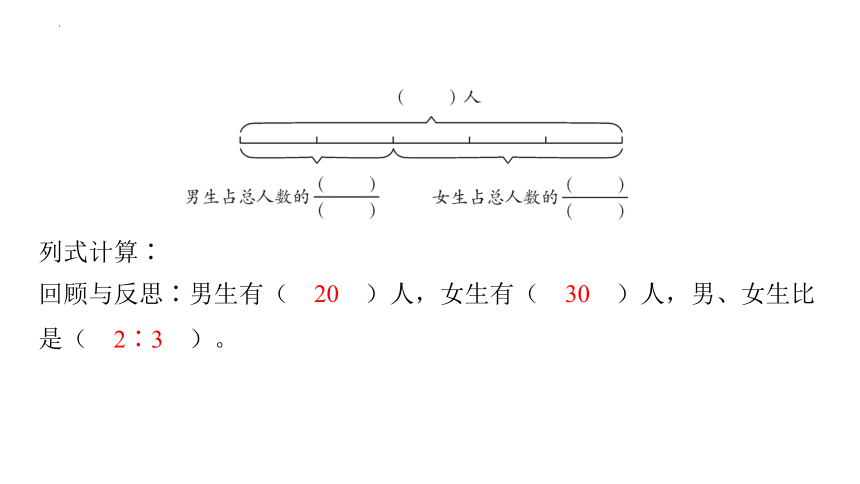
1. (广州市从化区)文明路小学50位同学参加经典美文诵读比赛,其中男、女生人数比是2∶3,男、女生各有多少人?
阅读与理解∶“男、女生人数比是2∶3”就是说,把50人平均分成( 5 )份,其中男生占( 2 )份,女生占( 3 )份。
分析与解答∶50×=20(人);50×=30(人);
5
2
3
50×=20(人);50×=30(人);
列式计算∶
回顾与反思∶男生有( 20 )人,女生有( 30 )人,男、女生比是( 2∶3 )。
20
30
2∶3
2. (揭阳市惠来县)笑笑按照说明书上1∶4的比调制了一杯100毫升的蜂蜜水给妈妈喝,妈妈尝了一口,说∶“笑笑,你把这杯水的甜味调得再淡些吧,浓度是10%就可以了。”同学们,你能帮笑笑想想办法吗?请通过列式计算说明你的方法。
100×÷10%-100=100(毫升)
需要加水100毫升。
考点2 比例的应用
考点精讲
1. 比例尺的应用
=比例尺 图上距离=比例尺×实际距离
实际距离=图上距离÷比例尺
2. 正、反比例解决问题
(1)审题,找出题中相关联的两个量。
(2)分析,判断题中相关联的两个量是成正比例关系还是成反比例关系。
(3)设未知数,列比例式。
(4)解比例式。
(5)检验,写答语。
真题精讲
例1(佛山市南海区)街心公园要建一个长方形的花坛,长120米,宽80米。请你按1∶2000的比例尺计算出花坛长和宽的图上距离。
【解析】图上距离=实际距离×比例尺
【答案】120米=12000厘米,80米=8000厘米
12000×=6(厘米),8000×=4(厘米)
答∶花坛长和宽的图上距离分别是6厘米和4厘米。
例2(东莞市)六年级办公室买进一些A4纸,如果平均每天用20张,可以用28天,实际每天节约用纸4张,这些A4纸实际可用多少天?(用比例解)
【解析】设这些A4纸实际可用x天,根据平均每天用纸张数×可用天数=总张数(一定),列出反比例算式解答即可。
【答案】解∶设这些A4纸实际可用x天。
(20-4)x=20×28
x=35
答∶这些A4纸实际可用35天。
跟踪训练
1. 北京到济南高速公路距离大约为430 km,北京到天津大约为120 km。一辆汽车从北京出发开往济南,当行驶到天津时用了1.5小时。按照这个速度,北京到济南全程需要多少小时?(用比例解)
解∶设北京到济南全程需要x小时。
120∶1.5=430∶x
120x=430×1.5
x=5.375
2. (中山市)学校装修一个地面为正方形的阅览室,用边长0.5米的正方形地砖铺地,正好需要144块。如果改用边长0.6米的正方形地砖铺地,需要多少块?(用比例解)
解∶设需要x块。
0.5×0.5×144=0.6×0.6×x
x=100
3. 在比例尺是1∶8000000的地图上,量得两地间的距离是6厘米,甲、乙两车同时从两地相对开出,3小时后相遇,甲、乙两车的速度比是3∶5,甲、乙两车每小时分别行驶多少千米?(用比例解)
6÷=48000000(厘米) 48000000厘米=480千米
解∶设甲车每小时行驶3x千米,乙车每小时行驶5x千米。
3x×3+5x×3=480
x=20
甲车∶20×3=60(千米) 乙车∶20×5=100(千米)
一、填空题。
1. 学校长跑队女运动员是男运动员人数的,女运动员人数与总人数的比是( 3∶11 )。
2. (东莞市)一个三角形三个内角度数的比是2∶2∶5。这个三角形按角分类属于( 钝角 )三角形,按边分类属于( 等腰 )三角形。
3. (阳江市江城区)被减数、减数与差的和是100,差与减数的比是1∶4,差是( 10 ),减数是( 40 ),被减数是( 50 )。
3∶11
钝角
等腰
10
40
50
4. (佛山市三水区)小明看一本故事书,已看的页数与未看页数的比是3∶5,未看的有40页,这本书共有( 64 )页,已看( 24 )页。
5. (潮州市湘桥区)如图是一张地图上的比例尺,将它转换为数值比例尺是( 1∶3000000 )。在这张地图上量得两地之间的距离为8.5厘米,则两地之间的实际距离是( 255 )千米。
64
24
1∶3000000
255
6. (大同市新荣区)小张和小杨是同一家快递公司的两名派件员。上周小张和小杨派送快递件数的比是7∶5,小张比小杨多派送了120件快递。上周小张和小杨一共派送了( 720 )件快递。
720
二、选择题。
1. 学校足球场长100米,宽64米,画在校园平面图上,长是5厘米。下面说法正确的是( D )。
A. 这幅图的比例尺是1∶20
B. 这幅图的比例尺是1∶200
C. 宽要画6.4厘米
D. 宽要画3.2厘米
D
2. (深圳市福田区)《庄子·天下篇》中“一尺之棰,日取其半,万世不竭”的意思是∶一尺长的木棒,第一天截取它长度的一半,以后每天都截取它前一天的一半,那么将永远也截取不完。如果按照这种截取方法,那么第3天截取的木棒长度与原来的木棒总长度的比是( D )。
A. 1∶2 B. 1∶3
C. 1∶6 D. 1∶8
D
3. (广州市白云区)六(1)班有学生44人,男生与女生人数的比可能是( D )。
A. 2∶3 B. 3∶4
C. 4∶5 D. 5∶6
4. 在比例尺是1∶3000000的地图上,量得A,B两港距离为12厘米,一艘货轮于上午7时以每小时24千米的速度从A港开向B港,到达B港的时间是( D )。
A. 16时 B. 18时
C. 20时 D. 22时
D
D
5. (广州市增城区)图中表示斑马和长颈鹿的奔跑情况。下面叙述错误的是( C )。
A. 如图是一个正比例关系的图象
B. 在20分钟时,它们路程相差8 km
C. 斑马和长颈鹿的速度之比是2∶3
D. 在15分钟时,长颈鹿跑了12 km
C
三、解决问题。
1. (广州市增城区)小芳练习口算的情况如图,照这样的速度,小芳6分钟能做多少道题?(用比例解)
解∶设小芳6分钟能做x道题。
x∶6=25∶2
2x=6×25
x=75
2. 一间房子要用方砖铺地,用面积是9平方分米的方砖,需用96块,如果改用边长是4分米的方砖,需用多少块?(用比例解)
解∶设需要x块。
4×4x=9×96
x=54
3. (济南市市中区)公园里有一个花坛,面积是100平方米,其中的30%种月季,剩下的面积按3∶4的比分别种玫瑰与牡丹,种玫瑰的面积是多少平方米?
100×(1-30%)×=30(平方米)
4. (韶关市曲江区)客车和货车同时从甲、乙两地的中间向相反的方向行驶,3小时后,客车到达甲地,货车离乙地还有40千米。已知货车和客车的速度比是5∶7,甲、乙两地相距多少千米?
40÷(1-)=140(千米)
140×2=280(千米)
答∶甲、乙两地相距280千米。
四、六年级三个志愿小队的同学收集废纸,第一小队收集的废纸占总数的25%,第二小队收集的废纸质量与第三小队收集的废纸质量的比是7∶8,第一小队比第三小队收集的废纸质量少45千克。三个小队一共收集了废纸多少千克?
解∶设三个小队一共收集了废纸x千克,则第一小队收集的废纸质量是25%x千克,第三小队收集的废纸质量是
(1-25%)x×=×x=x千克,
列方程∶x-25%x=45
x=300
五、(深圳市光明区)在比例尺是1∶5000000的地图上,量得甲地到乙地的图上距离是9厘米。李老师一家上午8∶00驾车从甲地前往乙地,小车平均每小时行驶100千米。
(1)上午11∶00时小车行驶至哪里?请在图中用“ ”标出,并简要说明理由。
11∶00-8∶00=3(小时)
100×3=300(千米)=30000000(厘米)
30000000×=6(厘米)
作图如下∶
(2)小车每行驶100千米消耗汽油8升,出发时油箱里有40升汽油,中途还需要再加油吗?(写出计算过程)
9÷=45000000(厘米)=450(千米)
450÷100×8=36(升)
36升<40升
所以中途不需要再加油。
(3)上午11∶00后,由于路上车流量增加,小车的平均速度下降了10%,那么李老师到达乙地的最早时间是几点几分?
100×(1-10%)=90(千米)
(450-300)÷90=1(小时)
1=1小时40分
11∶00+1小时40分=12∶40
