人教版六年级下册数学总复习比和比例的认识(课件)(共40张PPT)
文档属性
| 名称 | 人教版六年级下册数学总复习比和比例的认识(课件)(共40张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 22:34:19 | ||
图片预览












文档简介
(共40张PPT)
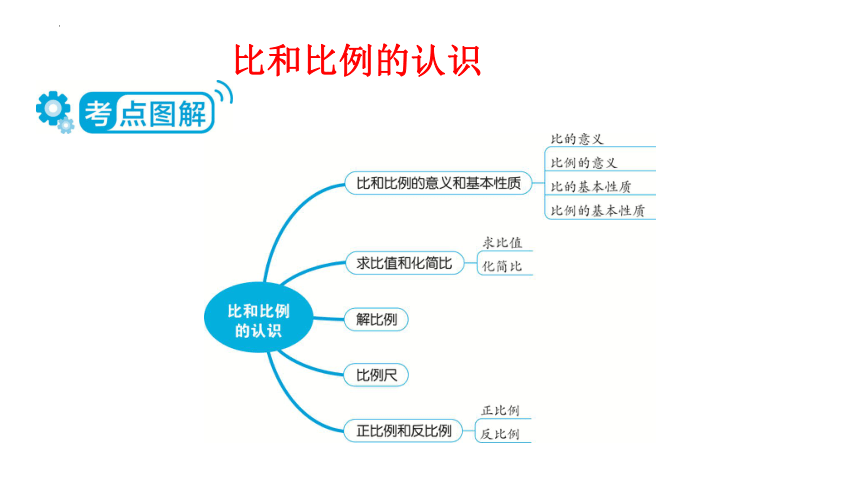
比和比例的认识
考点1 比和比例的意义和基本性质
考点精讲
1. 比的意义
(1)两个数相除又叫做两个数的比。
(2)比与分数、除法之间的联系和区别∶
联系 区别
比(a∶b或) 前项 比号(∶) 后项 比值 一种关系
分数() 分子 分数线(一) 分母 分数值 一种数或
一种关系
除法(a÷b) 被除数 除号(÷) 除数 商 一种运算
2. 比的基本性质
比的前项和后项同时乘或者除以相同的数(0除外),比值不变。
3. 比例的意义
表示两个比相等的式子叫做比例。 组成比例的四个数,叫做比例的项。
4. 比例的基本性质
在比例里,两个外项的积等于两个内项的积。用字母表示为∶若a∶b=c∶d(b,d均不为0),则有ad=bc。
真题精讲
例1(阳江市)汽车0.5小时行驶33千米,行驶的路程与时间的比是( ),比值是( )。
【解析】路程与时间的比是33∶0.5,两边同时乘2,化简即可;再用除法求出比值。
【答案】66∶1 66
例2(广州市番禺区)=15∶( )=( )∶24==5÷( )。
【解析】根据分数、除法和比的关系,把化为比的形式,然后根据比的基本性质,比的前项和后项同时乘或除以一个不为0的数,比值不变。据此解答即可。
【答案】18 20 30 6
例3(惠州市惠阳区)如果a×6=b×8,那么a∶b=( )∶( )。
【解析】根据比例的基本性质,两内项之积等于两外项之积,把b和8当作比例的内项,把a和6当作比例的外项,写出比例后化简即可。
【答案】4 3
跟踪训练
1. 10克盐溶于100克水中,盐与盐水的质量比是( B )。
A. 1∶10 B. 1∶11 C. 9∶10
2. 在2∶3中,如果前项增加10,要使比值不变,后项应增加( D )。
A. 12 B. 13 C. 14 D. 15
B
D
3. (广州市增城区)下面各选项中,各组数据或图形所对应的边的长度的比,能组成比例的是( D )。
A. 20∶5和1∶4
B. 0.6∶0.2和∶
C. (长与宽的比)
D. (两条直角边的比)
D
4. (惠州市惠阳区)在一个比例里,两个内项的积是18,一个外项是5,另一个外项是 ( 3.6 )。
3.6
考点2 求比值和化简比
考点精讲
1. 求比值
用比的前项除以后项求出商。
2. 化简比
根据比的基本性质把比化成最简单的整数比。它的结果必须是一个最简比,即前、后项是互质的整数。
真题精讲
例(佛山市顺德区)3∶0.75的比值是( ),把∶化成最简整数比是( )。
【解析】3∶0.75=3÷0.75=4;∶=(×40)∶(×40)=4∶5。
【答案】4 4∶5
跟踪训练
1. (汕尾市海丰县)聪聪在从家去学校的路上,他已经走了全程的,已经走的路程与所剩路程的最简整数比是( A )。
A. 5∶2 B. 2∶5 C. 7∶5
2. (广州市越秀区)买6支同样的钢笔要花36元,买5支同样的圆珠笔要花25元,钢笔和圆珠笔的单价之比是( 6∶5 ),比值是( 1.2 )。
A
6∶5
1.2
考点3 解比例
考点精讲
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
真题精讲
例(清远市清城区)解比例。
∶0.4=6∶x =
【解析】∶0.4=6∶x,根据比例的基本性质,原式化为x=0.4×6,再根据等式的性质2,方程两边同时除以即可;
=,根据比例的基本性质,原式化为7x=2.8×2,再根据等式的性质2,方程两边同时除以7即可。
【答案】
∶0.4=6∶x
解∶x=0.4×6
x=2.4
x=7.2
=
解∶7x=2.8×2
7x=5.6
x=0.8
跟踪训练
解比例。
54∶=x∶
=
x=
x=10
考点4 比例尺
考点精讲
1. 比例尺的意义
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
图上距离∶实际距离=比例尺或=比例尺。
2. 比例尺的分类
(1)数值比例尺,如∶1∶10000或。
(2)线段比例尺,如∶ 。
真题精讲
例(阳江市) 是( )比例尺,把它转化成数值比例尺为( );A,B两地相距280 km,画在这幅地图上长( ) cm。
【解析】由图可知是线段比例尺。图上1 cm表示实际距离50 km,依据“比例尺=图上距离∶实际距离”,改写成数值比例尺为1 cm∶50 km=1∶5000000。依据“图上距离=实际距离×比例尺”求得A,B两地之间的图上距离为28000000×=5.6(cm)。
【答案】 线段 1∶5000000 5.6
跟踪训练
1. (清远市清城区)一幅地图的比例尺是1∶5000000,用线段比例尺表示正确的是( B )。
A. B.
C. D.
2. (珠海市香洲区)实验小学的操场长108米,宽72米,在练习本上画平面图,比较合适的比例尺是( B )。
A. 1∶200 B. 1∶2000 C. 1∶20000
B
B
3. (百色市)设计人员把一个长5 mm的零件画在图纸上长为25 cm,这幅图纸的比例尺是( C )。
A. 1∶5
B. 5∶1
C. 50∶1
D. 1∶50
C
考点5 正比例和反比例
考点精讲
正比例和反比例的区别和联系
正比例 反比例
相同点 两种相关联的量,一种量变化,另一种量也随着变化
不 同 点 特征 两种量中,相对应的两个数的比值一定 两种量中,相对应的两个数的积一定
关系式 =k(一定) xy=k(一定)
真题精讲
例(深圳市福田区)下面两种量成反比例关系的是( )。
A. 总路程一定,已行驶的路程和剩下的路程
B. 圆锥的底面积一定,圆锥的体积与高
C. 全班人数一定,出勤人数与出勤率
D. 完成总时间一定,每个零件所需要时间与所做零件个数
【解析】两种相关联的量成什么比例,就看这两种变化的量是比值一定,还是乘积一定。如果比值一定,成正比例;如果乘积一定,成反比例。
A. 总路程=已行驶的路程+剩下的路程,已行驶的路程和剩下的路程不成比例。
B. 圆锥的体积=×底面积×高,圆锥的体积÷高=×底面积(一定),圆锥的体积与高成正比例。
C. 出勤人数÷出勤率=全班人数(一定),出勤人数与出勤率成正比例。
D. 每个零件所需时间×所做零件个数=完成总时间(一定),每个零件所需时间与所做零件个数成反比例。
【答案】D
跟踪训练
1. (肇庆市端州区)A=2B,A和B成( 正 )比例;9÷A=B,A和B成( 反 )比例。
2. (吉林市舒兰市)下列选项中的两种量成反比例关系的是( C )。
A. 一本书看过的页数和剩余的页数
B. 圆的周长和直径
C. 长方形的面积一定,它的长和宽
D.行驶时间一定,速度和路程
正
反
C
3. (揭阳市惠来县)下面等式中,x和y成反比例的是( D )。
A. x+y=15 B. y=15x
C. x∶3=y∶5 D. x∶3=5∶y
D
一、填空题。
1. (中山市)参加北京冬奥会的运动员中有55%为男性运动员,45%为女性运动员,男女运动员人数的最简整数比是( 11∶9 ),比值是( )。
2. ( 3 )÷8==12∶( 32 )=( 0.375 )(填小数)=37.5%。
3. 一个比例的两个外项分别是2.4和18,两个内项分别是x和36,则x=( )。
11∶9
3
32
0.375
1.2
4. 30 kg∶0.3 t的最简整数比是( 1∶10 ),如果将这个最简整数比的前项加上3,要使比值不变,后项应该加上( 30 )。
5. (衡阳市衡山县)若a∶b=1∶2,a∶c=1∶3,则a∶b∶c=( 1∶2 )。
6. (河源市紫金县)若5a=6b(a,b均不为0),则a∶b=( 6∶5 ),a与b成( 正 )比例。
7. 如表,如果x和y成正比例关系,“?”处应填( 6 );如果x和y成反比例关系,“?”处应填( 1.5 )。
1∶10
30
1∶2∶3
6∶5
正
6
1.5
x 3 ?
y 12 24
8. (渭南市华州区)一份稿件,甲单独打需10小时,乙单独打需12小时,甲和乙的工作效率比是( 6∶5 )。
9. 如图,两个正方形重叠部分的面积相当于小正方形面积的,相当于大正方形面积的,大、小正方形面积的比是( 5∶3 )。
6∶5
5∶3
二、选择题。
1. (东莞市)在一张图纸上,量得学校操场的长是6 cm,宽是3 cm,操场实际长120 m,宽60 m。这张图纸的比例尺是( D )。
A. 2000∶1 B. 1∶20
C. 1∶200 D. 1∶2000
D
2. 一个比的比值是,如果把它的前项和后项同时扩大到原来的3倍,这时的比值( A )。
A. 不变 B. 扩大到原来的3倍
C. 扩大到原来的9倍 D. 无法确定
A
3. (广州市白云区)下面哪组中的两个比可以组成比例( D )。
A. 6∶9和9∶12
B. ∶和0.2∶0.6
C. ∶和∶
D. 1.4∶2和28∶40
D
4. (深圳市南山区)在线段比例尺 中,下面说法正确的是( B )。
A. 图上距离是实际距离的
B. 图上1厘米表示实际距离5000000厘米
C. 实际距离是图上距离的100倍
D. 图上1厘米表示实际距离100000厘米
B
5. (深圳市龙华区)下列各种关系中,成反比例关系的是( B )。
A. 在一定时间里,每分钟生产的零件个数和生产零件的总个数
B. 三角形面积一定,它的底和高
C. 圆柱的底面半径一定,圆柱的高和圆柱的体积
D. 一捆50米长的电线,用去的长度与剩下的长度
B
6. 从甲堆煤中取出放入乙堆煤中,则两堆煤质量相等,原来甲、乙两堆煤的质量比是( A )。
A. 2∶1 B. 1∶2
C. 4∶1 D. 3∶1
A
三、判断题。
1. 当速度一定时,路程与时间成正比例。 ( √ )
2. (邯郸市武安市)9∶3=3是比例。 ( × )
3. (深圳市盐田区)某品牌钟表上需要一个长0.5毫米的零件,设计师将这个零件放大画在图纸上长5厘米,这幅图的比例尺是1∶100。 ( × )
4. (十堰市郧阳区)比例中,两个外项的积减去两个内项的积,差不为0。 ( × )
5. (铜仁市德江县)两个圆半径长度的比是2∶3,则它们的面积比是4∶9。 ( √ )
√
×
×
×
√
四、计算题。
1. 化简比并求比值。
20∶2.5
∶0.75
20∶2.5=8∶1;
比值为8。
∶0.75=16∶15;
比值为。
∶
45分钟∶小时
∶=3∶4;
比值为。
45分钟∶小时=9∶8;
比值为。
∶
kg∶30 g
∶=121∶36;
比值为。
kg∶30 g=25∶1;
比值为25。
2. 解比例。
18∶0.2=x∶
1.2∶x=
x=22.5
x=0.36
x∶=∶
=
x=
x=9
∶x=40%∶
∶=∶(4-x)
x=
x=
五、给8,16,32配上一个数,使得这四个数可以组成比例,这个数可以是哪些数?
解∶①16×8÷32=4 组成比例是∶4∶8=16∶32
②8×32÷16=16 组成比例是∶16∶8=32∶16
③16×32÷8=64 组成比例是∶8∶16=32∶64
所以这个数可以是4,16,64。
六、 如图,长方形A和B的面积分别是20平方厘米和60平方厘米,长方形C的面积比A大,求四个长方形的总面积。
20×(1+)=24(平方厘米)
设长方形D的面积
为x平方厘米。
20∶60=24∶x
20x=60×24
x=72
20+60+24+72=176(平方厘米)
A B
C D
比和比例的认识
考点1 比和比例的意义和基本性质
考点精讲
1. 比的意义
(1)两个数相除又叫做两个数的比。
(2)比与分数、除法之间的联系和区别∶
联系 区别
比(a∶b或) 前项 比号(∶) 后项 比值 一种关系
分数() 分子 分数线(一) 分母 分数值 一种数或
一种关系
除法(a÷b) 被除数 除号(÷) 除数 商 一种运算
2. 比的基本性质
比的前项和后项同时乘或者除以相同的数(0除外),比值不变。
3. 比例的意义
表示两个比相等的式子叫做比例。 组成比例的四个数,叫做比例的项。
4. 比例的基本性质
在比例里,两个外项的积等于两个内项的积。用字母表示为∶若a∶b=c∶d(b,d均不为0),则有ad=bc。
真题精讲
例1(阳江市)汽车0.5小时行驶33千米,行驶的路程与时间的比是( ),比值是( )。
【解析】路程与时间的比是33∶0.5,两边同时乘2,化简即可;再用除法求出比值。
【答案】66∶1 66
例2(广州市番禺区)=15∶( )=( )∶24==5÷( )。
【解析】根据分数、除法和比的关系,把化为比的形式,然后根据比的基本性质,比的前项和后项同时乘或除以一个不为0的数,比值不变。据此解答即可。
【答案】18 20 30 6
例3(惠州市惠阳区)如果a×6=b×8,那么a∶b=( )∶( )。
【解析】根据比例的基本性质,两内项之积等于两外项之积,把b和8当作比例的内项,把a和6当作比例的外项,写出比例后化简即可。
【答案】4 3
跟踪训练
1. 10克盐溶于100克水中,盐与盐水的质量比是( B )。
A. 1∶10 B. 1∶11 C. 9∶10
2. 在2∶3中,如果前项增加10,要使比值不变,后项应增加( D )。
A. 12 B. 13 C. 14 D. 15
B
D
3. (广州市增城区)下面各选项中,各组数据或图形所对应的边的长度的比,能组成比例的是( D )。
A. 20∶5和1∶4
B. 0.6∶0.2和∶
C. (长与宽的比)
D. (两条直角边的比)
D
4. (惠州市惠阳区)在一个比例里,两个内项的积是18,一个外项是5,另一个外项是 ( 3.6 )。
3.6
考点2 求比值和化简比
考点精讲
1. 求比值
用比的前项除以后项求出商。
2. 化简比
根据比的基本性质把比化成最简单的整数比。它的结果必须是一个最简比,即前、后项是互质的整数。
真题精讲
例(佛山市顺德区)3∶0.75的比值是( ),把∶化成最简整数比是( )。
【解析】3∶0.75=3÷0.75=4;∶=(×40)∶(×40)=4∶5。
【答案】4 4∶5
跟踪训练
1. (汕尾市海丰县)聪聪在从家去学校的路上,他已经走了全程的,已经走的路程与所剩路程的最简整数比是( A )。
A. 5∶2 B. 2∶5 C. 7∶5
2. (广州市越秀区)买6支同样的钢笔要花36元,买5支同样的圆珠笔要花25元,钢笔和圆珠笔的单价之比是( 6∶5 ),比值是( 1.2 )。
A
6∶5
1.2
考点3 解比例
考点精讲
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项,叫做解比例。
真题精讲
例(清远市清城区)解比例。
∶0.4=6∶x =
【解析】∶0.4=6∶x,根据比例的基本性质,原式化为x=0.4×6,再根据等式的性质2,方程两边同时除以即可;
=,根据比例的基本性质,原式化为7x=2.8×2,再根据等式的性质2,方程两边同时除以7即可。
【答案】
∶0.4=6∶x
解∶x=0.4×6
x=2.4
x=7.2
=
解∶7x=2.8×2
7x=5.6
x=0.8
跟踪训练
解比例。
54∶=x∶
=
x=
x=10
考点4 比例尺
考点精讲
1. 比例尺的意义
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
图上距离∶实际距离=比例尺或=比例尺。
2. 比例尺的分类
(1)数值比例尺,如∶1∶10000或。
(2)线段比例尺,如∶ 。
真题精讲
例(阳江市) 是( )比例尺,把它转化成数值比例尺为( );A,B两地相距280 km,画在这幅地图上长( ) cm。
【解析】由图可知是线段比例尺。图上1 cm表示实际距离50 km,依据“比例尺=图上距离∶实际距离”,改写成数值比例尺为1 cm∶50 km=1∶5000000。依据“图上距离=实际距离×比例尺”求得A,B两地之间的图上距离为28000000×=5.6(cm)。
【答案】 线段 1∶5000000 5.6
跟踪训练
1. (清远市清城区)一幅地图的比例尺是1∶5000000,用线段比例尺表示正确的是( B )。
A. B.
C. D.
2. (珠海市香洲区)实验小学的操场长108米,宽72米,在练习本上画平面图,比较合适的比例尺是( B )。
A. 1∶200 B. 1∶2000 C. 1∶20000
B
B
3. (百色市)设计人员把一个长5 mm的零件画在图纸上长为25 cm,这幅图纸的比例尺是( C )。
A. 1∶5
B. 5∶1
C. 50∶1
D. 1∶50
C
考点5 正比例和反比例
考点精讲
正比例和反比例的区别和联系
正比例 反比例
相同点 两种相关联的量,一种量变化,另一种量也随着变化
不 同 点 特征 两种量中,相对应的两个数的比值一定 两种量中,相对应的两个数的积一定
关系式 =k(一定) xy=k(一定)
真题精讲
例(深圳市福田区)下面两种量成反比例关系的是( )。
A. 总路程一定,已行驶的路程和剩下的路程
B. 圆锥的底面积一定,圆锥的体积与高
C. 全班人数一定,出勤人数与出勤率
D. 完成总时间一定,每个零件所需要时间与所做零件个数
【解析】两种相关联的量成什么比例,就看这两种变化的量是比值一定,还是乘积一定。如果比值一定,成正比例;如果乘积一定,成反比例。
A. 总路程=已行驶的路程+剩下的路程,已行驶的路程和剩下的路程不成比例。
B. 圆锥的体积=×底面积×高,圆锥的体积÷高=×底面积(一定),圆锥的体积与高成正比例。
C. 出勤人数÷出勤率=全班人数(一定),出勤人数与出勤率成正比例。
D. 每个零件所需时间×所做零件个数=完成总时间(一定),每个零件所需时间与所做零件个数成反比例。
【答案】D
跟踪训练
1. (肇庆市端州区)A=2B,A和B成( 正 )比例;9÷A=B,A和B成( 反 )比例。
2. (吉林市舒兰市)下列选项中的两种量成反比例关系的是( C )。
A. 一本书看过的页数和剩余的页数
B. 圆的周长和直径
C. 长方形的面积一定,它的长和宽
D.行驶时间一定,速度和路程
正
反
C
3. (揭阳市惠来县)下面等式中,x和y成反比例的是( D )。
A. x+y=15 B. y=15x
C. x∶3=y∶5 D. x∶3=5∶y
D
一、填空题。
1. (中山市)参加北京冬奥会的运动员中有55%为男性运动员,45%为女性运动员,男女运动员人数的最简整数比是( 11∶9 ),比值是( )。
2. ( 3 )÷8==12∶( 32 )=( 0.375 )(填小数)=37.5%。
3. 一个比例的两个外项分别是2.4和18,两个内项分别是x和36,则x=( )。
11∶9
3
32
0.375
1.2
4. 30 kg∶0.3 t的最简整数比是( 1∶10 ),如果将这个最简整数比的前项加上3,要使比值不变,后项应该加上( 30 )。
5. (衡阳市衡山县)若a∶b=1∶2,a∶c=1∶3,则a∶b∶c=( 1∶2 )。
6. (河源市紫金县)若5a=6b(a,b均不为0),则a∶b=( 6∶5 ),a与b成( 正 )比例。
7. 如表,如果x和y成正比例关系,“?”处应填( 6 );如果x和y成反比例关系,“?”处应填( 1.5 )。
1∶10
30
1∶2∶3
6∶5
正
6
1.5
x 3 ?
y 12 24
8. (渭南市华州区)一份稿件,甲单独打需10小时,乙单独打需12小时,甲和乙的工作效率比是( 6∶5 )。
9. 如图,两个正方形重叠部分的面积相当于小正方形面积的,相当于大正方形面积的,大、小正方形面积的比是( 5∶3 )。
6∶5
5∶3
二、选择题。
1. (东莞市)在一张图纸上,量得学校操场的长是6 cm,宽是3 cm,操场实际长120 m,宽60 m。这张图纸的比例尺是( D )。
A. 2000∶1 B. 1∶20
C. 1∶200 D. 1∶2000
D
2. 一个比的比值是,如果把它的前项和后项同时扩大到原来的3倍,这时的比值( A )。
A. 不变 B. 扩大到原来的3倍
C. 扩大到原来的9倍 D. 无法确定
A
3. (广州市白云区)下面哪组中的两个比可以组成比例( D )。
A. 6∶9和9∶12
B. ∶和0.2∶0.6
C. ∶和∶
D. 1.4∶2和28∶40
D
4. (深圳市南山区)在线段比例尺 中,下面说法正确的是( B )。
A. 图上距离是实际距离的
B. 图上1厘米表示实际距离5000000厘米
C. 实际距离是图上距离的100倍
D. 图上1厘米表示实际距离100000厘米
B
5. (深圳市龙华区)下列各种关系中,成反比例关系的是( B )。
A. 在一定时间里,每分钟生产的零件个数和生产零件的总个数
B. 三角形面积一定,它的底和高
C. 圆柱的底面半径一定,圆柱的高和圆柱的体积
D. 一捆50米长的电线,用去的长度与剩下的长度
B
6. 从甲堆煤中取出放入乙堆煤中,则两堆煤质量相等,原来甲、乙两堆煤的质量比是( A )。
A. 2∶1 B. 1∶2
C. 4∶1 D. 3∶1
A
三、判断题。
1. 当速度一定时,路程与时间成正比例。 ( √ )
2. (邯郸市武安市)9∶3=3是比例。 ( × )
3. (深圳市盐田区)某品牌钟表上需要一个长0.5毫米的零件,设计师将这个零件放大画在图纸上长5厘米,这幅图的比例尺是1∶100。 ( × )
4. (十堰市郧阳区)比例中,两个外项的积减去两个内项的积,差不为0。 ( × )
5. (铜仁市德江县)两个圆半径长度的比是2∶3,则它们的面积比是4∶9。 ( √ )
√
×
×
×
√
四、计算题。
1. 化简比并求比值。
20∶2.5
∶0.75
20∶2.5=8∶1;
比值为8。
∶0.75=16∶15;
比值为。
∶
45分钟∶小时
∶=3∶4;
比值为。
45分钟∶小时=9∶8;
比值为。
∶
kg∶30 g
∶=121∶36;
比值为。
kg∶30 g=25∶1;
比值为25。
2. 解比例。
18∶0.2=x∶
1.2∶x=
x=22.5
x=0.36
x∶=∶
=
x=
x=9
∶x=40%∶
∶=∶(4-x)
x=
x=
五、给8,16,32配上一个数,使得这四个数可以组成比例,这个数可以是哪些数?
解∶①16×8÷32=4 组成比例是∶4∶8=16∶32
②8×32÷16=16 组成比例是∶16∶8=32∶16
③16×32÷8=64 组成比例是∶8∶16=32∶64
所以这个数可以是4,16,64。
六、 如图,长方形A和B的面积分别是20平方厘米和60平方厘米,长方形C的面积比A大,求四个长方形的总面积。
20×(1+)=24(平方厘米)
设长方形D的面积
为x平方厘米。
20∶60=24∶x
20x=60×24
x=72
20+60+24+72=176(平方厘米)
A B
C D
