第1章 勾股定理 复习训练(无答案) 2023-2024学年北师大版八年级数学上册
文档属性
| 名称 | 第1章 勾股定理 复习训练(无答案) 2023-2024学年北师大版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 16:22:06 | ||
图片预览

文档简介
北师大版八上勾股定理复习训练
一.选择题
1.一个直角三角形,有两边长分别为6和8,下列说法正确的是( )
A. 第三边一定为10 B. 三角形的周长为25
C. 三角形的面积为48 D. 第三边可能为10
2.以下列各组数的长为边作三角形,不能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.6,8,10 D.9,12,15
3.如图,在Rt△ABC中,∠ABC=90°,BC=1,以点A为圆心,交数轴于点E,则点E表示的实数是( )
A. B.﹣1 C.+1 D.1﹣
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87 C.119 D.81
5.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米 B.1.7米 C.1.8米 D.0.6米
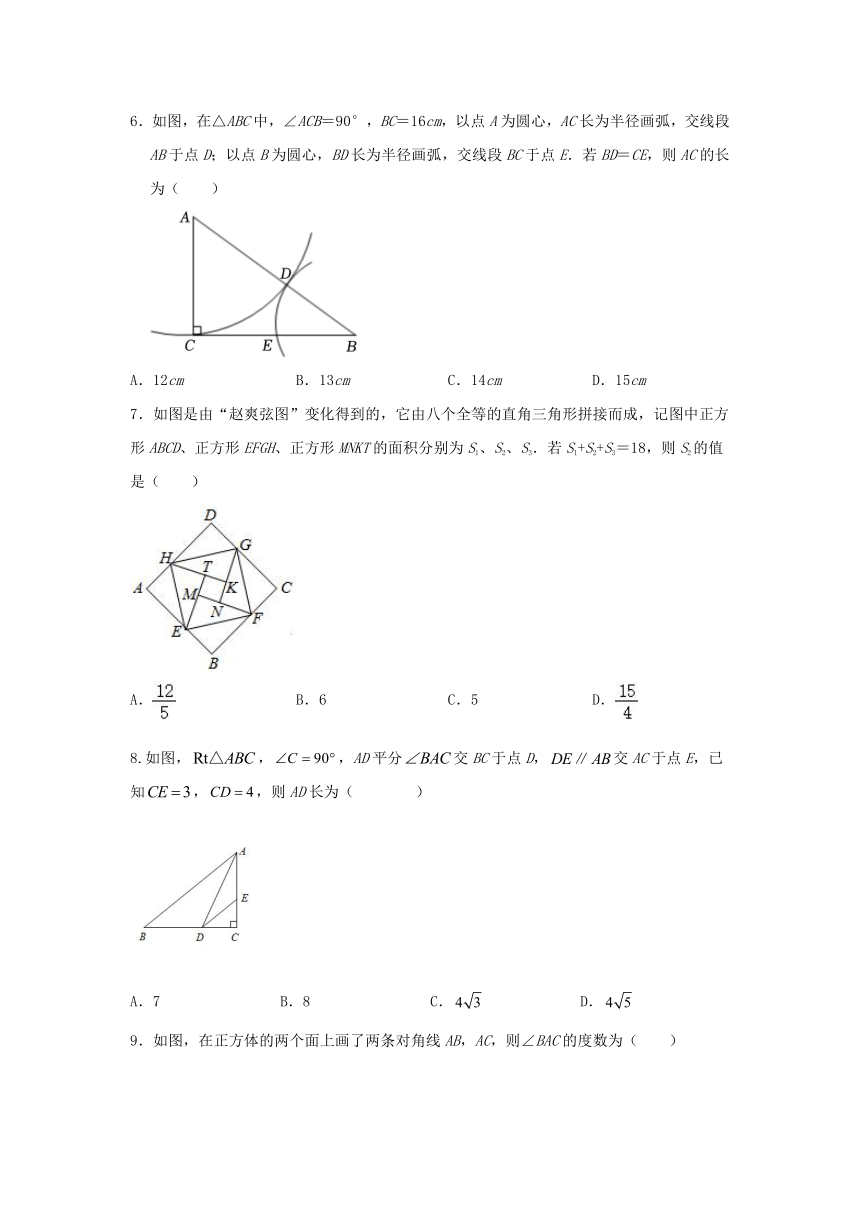
6.如图,在△ABC中,∠ACB=90°,BC=16cm,以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E.若BD=CE,则AC的长为( )
A.12cm B.13cm C.14cm D.15cm
7.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=18,则S2的值是( )
A. B.6 C.5 D.
8.如图,,,AD平分交BC于点D,交AC于点E,已知,,则AD长为( )
A.7 B.8 C. D.
9.如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC的度数为( )
A.135° B.90° C.75° D.60°
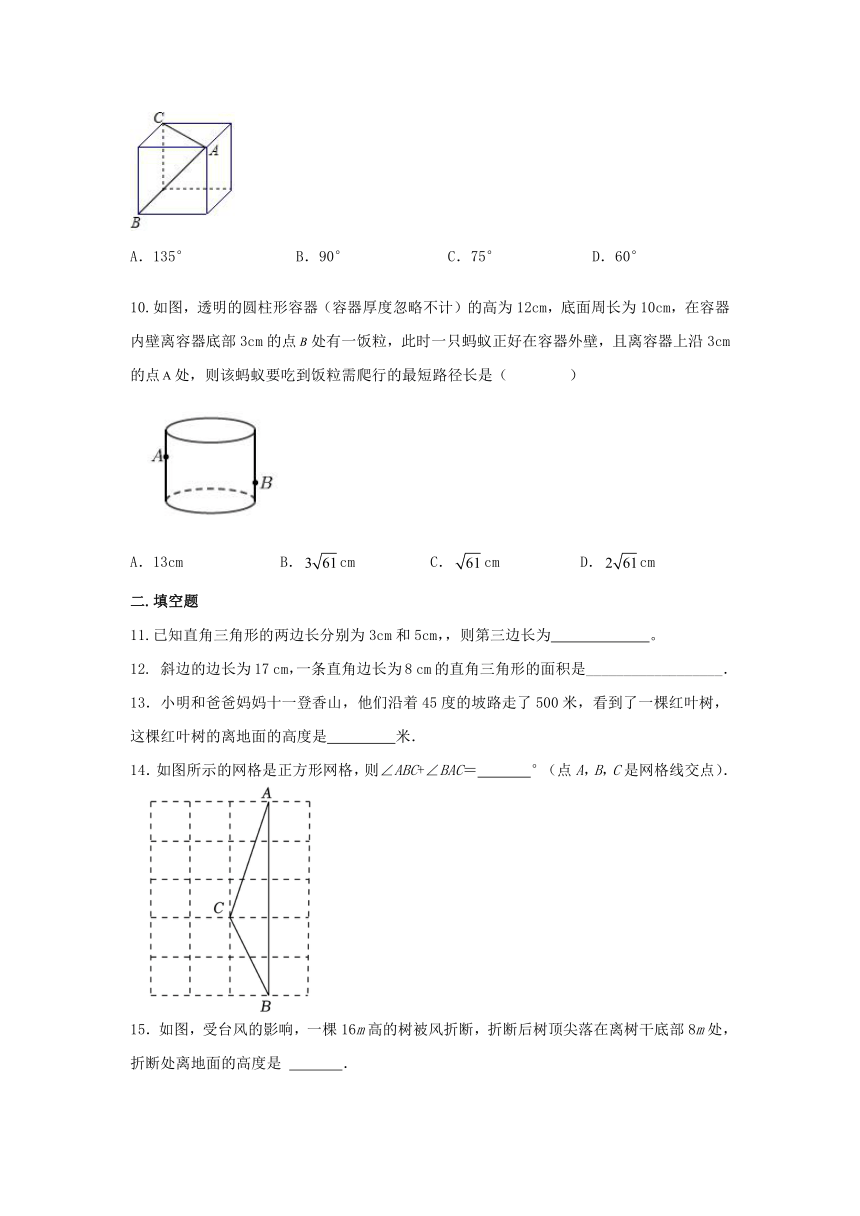
10.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点处,则该蚂蚁要吃到饭粒需爬行的最短路径长是( )
A.13cm B.cm C.cm D.cm
二.填空题
11.已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。
12. 斜边的边长为17 cm,一条直角边长为8 cm的直角三角形的面积是__________________.
13.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米.
14.如图所示的网格是正方形网格,则∠ABC+∠BAC= °(点A,B,C是网格线交点).
15.如图,受台风的影响,一棵16m高的树被风折断,折断后树顶尖落在离树干底部8m处,折断处离地面的高度是 .
16.如图,有两棵树,一棵高米,另一棵高米,两树相距米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米.
三.解答题
17.如图,正方形网格中,每个小正方形的边长为1.
(1)求AB、BC、AC的长;
(2)求∠ABC的度数.
18.如图,在四边形ABCD中,AB=24,AD=7,BC=15,CD=20,且∠C=90°,求四边形ABCD的面积.
19.某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.
(1)求小岛两端A,B的距离.
(2)过点C作CF⊥AB交AB的延长线于点F,求值.
20.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间的距离为,若规定小汽车在该城市街路上的行驶速度不得超过,则这辆小汽车超速了吗?
(参考数据转换:
21.如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男孩拽着绳子另一端向右走,绳端从移动到,同时小船从移动到,且绳长始终保持不变.、、三点在一条直线上,.回答下列问题:
(1)根据题意可知: (填“>”、“<”、“=”).
(2)若米,米,米,求小男孩需向右移动的距离(结果保留根号).
一.选择题
1.一个直角三角形,有两边长分别为6和8,下列说法正确的是( )
A. 第三边一定为10 B. 三角形的周长为25
C. 三角形的面积为48 D. 第三边可能为10
2.以下列各组数的长为边作三角形,不能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.6,8,10 D.9,12,15
3.如图,在Rt△ABC中,∠ABC=90°,BC=1,以点A为圆心,交数轴于点E,则点E表示的实数是( )
A. B.﹣1 C.+1 D.1﹣
4.如图,在四边形ABCD中,∠DAB=∠BCD=90°,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4=( )
A.183 B.87 C.119 D.81
5.如图,八年级一班的同学准备测量校园人工湖的深度,他们把一根竹竿竖直插到水底,此时竹竿离岸边点C处的距离米.竹竿高出水面的部分长0.2米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则人工湖的深度为( )
A.1.5米 B.1.7米 C.1.8米 D.0.6米
6.如图,在△ABC中,∠ACB=90°,BC=16cm,以点A为圆心,AC长为半径画弧,交线段AB于点D;以点B为圆心,BD长为半径画弧,交线段BC于点E.若BD=CE,则AC的长为( )
A.12cm B.13cm C.14cm D.15cm
7.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=18,则S2的值是( )
A. B.6 C.5 D.
8.如图,,,AD平分交BC于点D,交AC于点E,已知,,则AD长为( )
A.7 B.8 C. D.
9.如图,在正方体的两个面上画了两条对角线AB,AC,则∠BAC的度数为( )
A.135° B.90° C.75° D.60°
10.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点处,则该蚂蚁要吃到饭粒需爬行的最短路径长是( )
A.13cm B.cm C.cm D.cm
二.填空题
11.已知直角三角形的两边长分别为3cm和5cm,,则第三边长为 。
12. 斜边的边长为17 cm,一条直角边长为8 cm的直角三角形的面积是__________________.
13.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是 米.
14.如图所示的网格是正方形网格,则∠ABC+∠BAC= °(点A,B,C是网格线交点).
15.如图,受台风的影响,一棵16m高的树被风折断,折断后树顶尖落在离树干底部8m处,折断处离地面的高度是 .
16.如图,有两棵树,一棵高米,另一棵高米,两树相距米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行 米.
三.解答题
17.如图,正方形网格中,每个小正方形的边长为1.
(1)求AB、BC、AC的长;
(2)求∠ABC的度数.
18.如图,在四边形ABCD中,AB=24,AD=7,BC=15,CD=20,且∠C=90°,求四边形ABCD的面积.
19.某海上有一小岛,为了测量小岛两端A,B的距离,测量人员设计了一种测量方法,如图,已知B是CD的中点,E是BA延长线上的一点,且∠CED=90°,测得AE=16.6海里,DE=60海里,CE=80海里.
(1)求小岛两端A,B的距离.
(2)过点C作CF⊥AB交AB的延长线于点F,求值.
20.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪处的正前方的处,过了后,测得小汽车与车速检测仪间的距离为,若规定小汽车在该城市街路上的行驶速度不得超过,则这辆小汽车超速了吗?
(参考数据转换:
21.如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男孩拽着绳子另一端向右走,绳端从移动到,同时小船从移动到,且绳长始终保持不变.、、三点在一条直线上,.回答下列问题:
(1)根据题意可知: (填“>”、“<”、“=”).
(2)若米,米,米,求小男孩需向右移动的距离(结果保留根号).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
