1.2.4 绝对值 课件 (共21张PPT)人教版数学七年级上册
文档属性
| 名称 | 1.2.4 绝对值 课件 (共21张PPT)人教版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 12:48:00 | ||
图片预览








文档简介
(共21张PPT)
1.2有理数
1.2.4绝对值第二课时
知识回顾
绝对值的定义:
一般地,数轴上表示
叫做数a的绝对值
记作
绝对值的性质:
一个正数的绝对值是
;即当时,那么
一个负数的绝对值是
;即当
时,那么
0的绝对值是;即当时,那么
学习目标
1.通过探究得出有理数大小的比较方法.(重点)
2.能利用数轴及绝对值的知识,比较两个有理数
的大小.(难点)
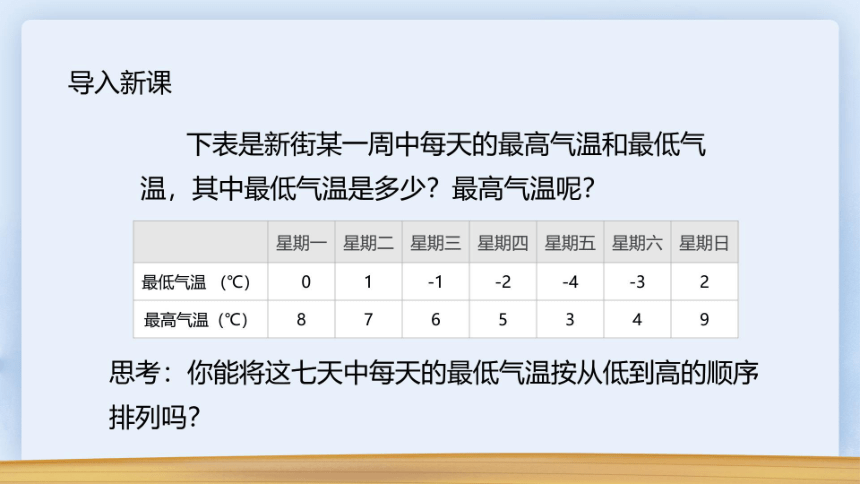
导入新课
下表是新街某一周中每天的最高气温和最低气
温,其中最低气温是多少?最高气温呢?
星期
星期二
星期三
星期四
星期五
星期六
星期日
最低气温
(C)
0
1
-1
-2
-4
-3
2
最高气温(℃)
8
7
6
5
3
4
9
思考:你能将这七天中每天的最低气温按从低到高的顺序
排列吗?
一、借助数轴扯比较有理数的大小
星期一
星期二
星期三
星期四
星期五
星期六
星期日
最低气温
(℃)
0
1
-1
-2
-4
-3
2
这七天中每天的最低气温按从低到高排列为:
越来越大
-5-4-3-2-10123456
有理数大小的比较方法1
数轴比较法:
这是重点
在数轴上表示的两个数,右边的数总比左边的数大
小
大
-5-4-3-2-10123456
思考:有没有最大的有理数?有没有最小的有理数?
为什么?
例1在数轴上表示数-3,-5,4,0,并比较它们的大小,将
它们按从小到大的顺序用“<”号连接,
解:-3,-5,4,0在数轴上表示如图:
-5
-4-3-2-1
01
23
4
将它们按从小到大的顺序排列为:
-5≤-3<0<4
针对训练:
如图,数轴上A,B,C三点表示的数分别为
a,b,c,侧它们的大小关系是()
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
A
B
101
二、运用法测比较有理数的大小
问题:
对与
数这三类数,它们之间有什么大小
关系
之间如何比较大小?
结论:
这是重点
(1)正数大于0,1
负数小于0,正数大于负数:
(2)两个负数,绝对值大的反而小.
例如,10,0-1,1-1,-1-2.
例2比较下列各数的大小
(1)-(-1)和-(+2):
②和号
8
3)(-0.3)和131
(1)-(-1)和-(+2);
异号两数比较要
考虑它们的正负!
解:先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,所以1>-2,即
-(-1)>-(+2).
1.2有理数
1.2.4绝对值第二课时
知识回顾
绝对值的定义:
一般地,数轴上表示
叫做数a的绝对值
记作
绝对值的性质:
一个正数的绝对值是
;即当时,那么
一个负数的绝对值是
;即当
时,那么
0的绝对值是;即当时,那么
学习目标
1.通过探究得出有理数大小的比较方法.(重点)
2.能利用数轴及绝对值的知识,比较两个有理数
的大小.(难点)
导入新课
下表是新街某一周中每天的最高气温和最低气
温,其中最低气温是多少?最高气温呢?
星期
星期二
星期三
星期四
星期五
星期六
星期日
最低气温
(C)
0
1
-1
-2
-4
-3
2
最高气温(℃)
8
7
6
5
3
4
9
思考:你能将这七天中每天的最低气温按从低到高的顺序
排列吗?
一、借助数轴扯比较有理数的大小
星期一
星期二
星期三
星期四
星期五
星期六
星期日
最低气温
(℃)
0
1
-1
-2
-4
-3
2
这七天中每天的最低气温按从低到高排列为:
越来越大
-5-4-3-2-10123456
有理数大小的比较方法1
数轴比较法:
这是重点
在数轴上表示的两个数,右边的数总比左边的数大
小
大
-5-4-3-2-10123456
思考:有没有最大的有理数?有没有最小的有理数?
为什么?
例1在数轴上表示数-3,-5,4,0,并比较它们的大小,将
它们按从小到大的顺序用“<”号连接,
解:-3,-5,4,0在数轴上表示如图:
-5
-4-3-2-1
01
23
4
将它们按从小到大的顺序排列为:
-5≤-3<0<4
针对训练:
如图,数轴上A,B,C三点表示的数分别为
a,b,c,侧它们的大小关系是()
A.a>b>c B.b>c>a C.c>a>b D.b>a>c
A
B
101
二、运用法测比较有理数的大小
问题:
对与
数这三类数,它们之间有什么大小
关系
之间如何比较大小?
结论:
这是重点
(1)正数大于0,1
负数小于0,正数大于负数:
(2)两个负数,绝对值大的反而小.
例如,10,0-1,1-1,-1-2.
例2比较下列各数的大小
(1)-(-1)和-(+2):
②和号
8
3)(-0.3)和131
(1)-(-1)和-(+2);
异号两数比较要
考虑它们的正负!
解:先化简,-(-1)=1,-(+2)=-2
因为正数大于负数,所以1>-2,即
-(-1)>-(+2).
