鲁教版(五四学制)六年级下册 6.6 平方差公式(25张PPT)
文档属性
| 名称 | 鲁教版(五四学制)六年级下册 6.6 平方差公式(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 17:10:49 | ||
图片预览








文档简介
(共25张PPT)
平方差公式
目录
01
学习目标
02
知识讲解
03
课堂练习
03
课堂总结
PART 01
学习目标
学习目标
经历探索平方差公式的过程,会推导平方差公式.
理解平方差公式的结构特征,灵活应用平方差公式.
PART 02
知识讲解
导入
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
回忆:多项式与多项式相乘的法则
知识讲解
(x+1)(x-1); (2) (a+2)(a-2);
(3) (3-x)(3+x) ; (4) (2x+1)(2x-1).
观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?
等号的左边:两个数的和与差的乘积,
等号的右边:这两个数的平方差.
= a2-4
=4 x2-1
观察思考
知识讲解
平方差公式:
(a+b)(a-b)=
a2-b2.
两个数的和与这两个数的差的乘积,等于这两个数的平方差.
(a+b)(a-b)=
a2- b2 .
a2- ab+ab- b2=
归纳
知识讲解
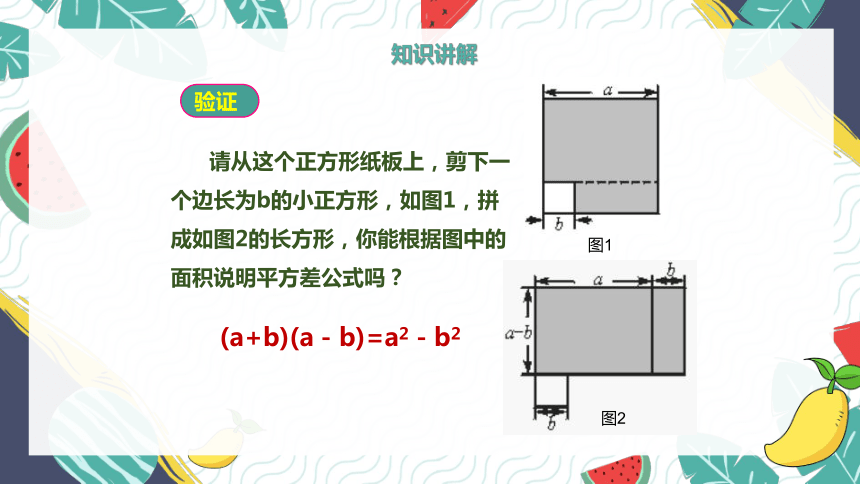
请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?
(a+b)(a-b)=a2-b2
图1
图2
验证
知识讲解
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
下列式子可用平方差公式计算吗 为什么
如果能够,怎样计算
(两组相反项 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
(6)( 4a 1)(4a 1)
(能)
(两组相反项 )
(两组相同项 )
(两组相同项 )
知识讲解
利用平方差公式计算:
(1) (5+6x)(5 6x);(2) (x+2y)(x 2y); (3)( m+n)( m n).
解: (1) (5+6x)(5 6x)=
5
5
相同项
52
平方
6x
6x
相反项
平方
要用括号把这个数整个括起来,
注意
当“相同项或相反项”是一分数或是数与字母的乘积时,
再平方;
( )2
6x
=
25
最后的结果要去掉括号。
36x2 ;
(2) (x+2y) (x 2y)
=
x
x
x2
( )2
2y
2y
2y
=
x2 4y2 ;
例题
【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) .(2) (b+2a)(2a-b).
【解析】 (1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
只有符合(a+b) (a- b)的
形式才能用平方差公式
知识讲解
计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5).
【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.
(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-4-y2-5y+y+5
=-4y+1.
跟踪训练
1.下列多项式乘法中,能用平方差公式计算的是 ( )
(1)(x+1)(1+x); (2)(a+b)(b-a);
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2).
(2)(5)(6)
跟踪训练
2.利用平方差公式计算:
原式=(-2y-x)(-2y+x)
= 4y2-x2.
【解析】原式=(5+2x)(5-2x)
= 25-4x2.
【解析】原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x.
平方差公式的逆用
a2-b2 = (a+b)(a-b)
【解析】
知识讲解
【解析】原式=(0.5-x)(0.5+x)(x2 +0.25)
=( 0.25-x2)( 0.25+x2)
=0.062 5-x4.
(5)100.5×99.5.
【解析】原式=(100+0.5)(100-0.5)
=10 000-0.25
=9 999.75.
(4)(0.5-x)(x+0.5)(x2+0.25)
PART 03
课堂练习
随堂练习
1.(眉山·中考)下列运算中正确的是( )A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 .
2.(威海·中考)已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.
随堂练习
3.(湖州·中考)将图甲中阴影部分的小长方形变换到
图乙位置,你能根据两个图形的面积关系得到的数学公式是
___________.
【解析】图甲的面积=(a+b)(a-b),图乙的面积=a(a-b)+b(a-b)=a2-ab+ab-b2=a2-b2.
答案:(a+b)(a-b)=a2-b2
随堂练习
原式=(100-1)(100+1)×10001
=(10 000-1)(10 000+1)
=100 000 000-1
=99 999 999.
4.计算 99×101×10001.
【解析】
随堂练习
5.化简:(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16).
原式=(x2-y2 )( x2+y2)(x4+y4)(x8+y8)(x16+y16)
=(x4-y4)(x4+y4)(x8+y8)(x16+y16)
=(x8-y8)(x8+y8)(x16+y16)
=(x16-y16)(x16+y16)
= x32-y32.
【解析】
PART 04
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
平方差公式:
(a+b)(a-b)=a2-b2.
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式的逆用: a2-b2 = (a+b)(a-b)
(1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方
减去第二项的平方.
(3) 公式中的 a和b 可以代表数,
也可以是代数式.
特征结构
(a+b)(a b)=
a2 b2.
课堂小结
感谢观看
平方差公式
目录
01
学习目标
02
知识讲解
03
课堂练习
03
课堂总结
PART 01
学习目标
学习目标
经历探索平方差公式的过程,会推导平方差公式.
理解平方差公式的结构特征,灵活应用平方差公式.
PART 02
知识讲解
导入
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn.
回忆:多项式与多项式相乘的法则
知识讲解
(x+1)(x-1); (2) (a+2)(a-2);
(3) (3-x)(3+x) ; (4) (2x+1)(2x-1).
观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?
等号的左边:两个数的和与差的乘积,
等号的右边:这两个数的平方差.
= a2-4
=4 x2-1
观察思考
知识讲解
平方差公式:
(a+b)(a-b)=
a2-b2.
两个数的和与这两个数的差的乘积,等于这两个数的平方差.
(a+b)(a-b)=
a2- b2 .
a2- ab+ab- b2=
归纳
知识讲解
请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?
(a+b)(a-b)=a2-b2
图1
图2
验证
知识讲解
(1) (a+b)( a b) ;
(2) (a b)(b a) ;
(3) (a+2b)(2b+a);
(4) (a b)(a+b) ;
(5) ( 2x+y)(y 2x).
(不能)
下列式子可用平方差公式计算吗 为什么
如果能够,怎样计算
(两组相反项 )
(不能)
(不能)
(能)
(a2 b2)=
a2 + b2 ;
(不能)
(6)( 4a 1)(4a 1)
(能)
(两组相反项 )
(两组相同项 )
(两组相同项 )
知识讲解
利用平方差公式计算:
(1) (5+6x)(5 6x);(2) (x+2y)(x 2y); (3)( m+n)( m n).
解: (1) (5+6x)(5 6x)=
5
5
相同项
52
平方
6x
6x
相反项
平方
要用括号把这个数整个括起来,
注意
当“相同项或相反项”是一分数或是数与字母的乘积时,
再平方;
( )2
6x
=
25
最后的结果要去掉括号。
36x2 ;
(2) (x+2y) (x 2y)
=
x
x
x2
( )2
2y
2y
2y
=
x2 4y2 ;
例题
【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) .(2) (b+2a)(2a-b).
【解析】 (1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2)(b+2a)(2a-b)
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
只有符合(a+b) (a- b)的
形式才能用平方差公式
知识讲解
计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5).
【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.
(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-4-y2-5y+y+5
=-4y+1.
跟踪训练
1.下列多项式乘法中,能用平方差公式计算的是 ( )
(1)(x+1)(1+x); (2)(a+b)(b-a);
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2).
(2)(5)(6)
跟踪训练
2.利用平方差公式计算:
原式=(-2y-x)(-2y+x)
= 4y2-x2.
【解析】原式=(5+2x)(5-2x)
= 25-4x2.
【解析】原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x.
平方差公式的逆用
a2-b2 = (a+b)(a-b)
【解析】
知识讲解
【解析】原式=(0.5-x)(0.5+x)(x2 +0.25)
=( 0.25-x2)( 0.25+x2)
=0.062 5-x4.
(5)100.5×99.5.
【解析】原式=(100+0.5)(100-0.5)
=10 000-0.25
=9 999.75.
(4)(0.5-x)(x+0.5)(x2+0.25)
PART 03
课堂练习
随堂练习
1.(眉山·中考)下列运算中正确的是( )A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 .
2.(威海·中考)已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.
随堂练习
3.(湖州·中考)将图甲中阴影部分的小长方形变换到
图乙位置,你能根据两个图形的面积关系得到的数学公式是
___________.
【解析】图甲的面积=(a+b)(a-b),图乙的面积=a(a-b)+b(a-b)=a2-ab+ab-b2=a2-b2.
答案:(a+b)(a-b)=a2-b2
随堂练习
原式=(100-1)(100+1)×10001
=(10 000-1)(10 000+1)
=100 000 000-1
=99 999 999.
4.计算 99×101×10001.
【解析】
随堂练习
5.化简:(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16).
原式=(x2-y2 )( x2+y2)(x4+y4)(x8+y8)(x16+y16)
=(x4-y4)(x4+y4)(x8+y8)(x16+y16)
=(x8-y8)(x8+y8)(x16+y16)
=(x16-y16)(x16+y16)
= x32-y32.
【解析】
PART 04
课堂小结
课堂小结
通过本课时的学习,需要我们掌握:
平方差公式:
(a+b)(a-b)=a2-b2.
即两个数的和与这两个数的差的积,等于这两个数的平方差.
平方差公式的逆用: a2-b2 = (a+b)(a-b)
(1) 公式左边两个二项式必须是
相同两数的和与差相乘;
且左边两括号内的第一项相等、
第二项符号相反[互为相反数(式)];
(2) 公式右边是这两个数的平方差;
即右边是左边括号内的第一项的平方
减去第二项的平方.
(3) 公式中的 a和b 可以代表数,
也可以是代数式.
特征结构
(a+b)(a b)=
a2 b2.
课堂小结
感谢观看
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
