鲁教版(五四学制)六年级下册6.7完全平方公式课件(共25张PPT)
文档属性
| 名称 | 鲁教版(五四学制)六年级下册6.7完全平方公式课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 17:10:12 | ||
图片预览






文档简介
(共25张PPT)
完全平方公式
01
学习目标
02
回顾与思考
03
新课导入
04
完全平方公式
目录
CONTENTS
05
课堂总结
学习目标
学习目标
一、学习目标
1.完全平方公式的推导及其应用.
2.完全平方公式的几何背景.
3.经历探索完全平方公式的过程,进一步发展符号感和推理能力,培养有条理的思考和表达能力.
二、学习重点
1.完全平方公式的推导过程、结构特点、语言表述、几何解释.
2.完全平方公式的应用.
回顾与思考
回顾与思考
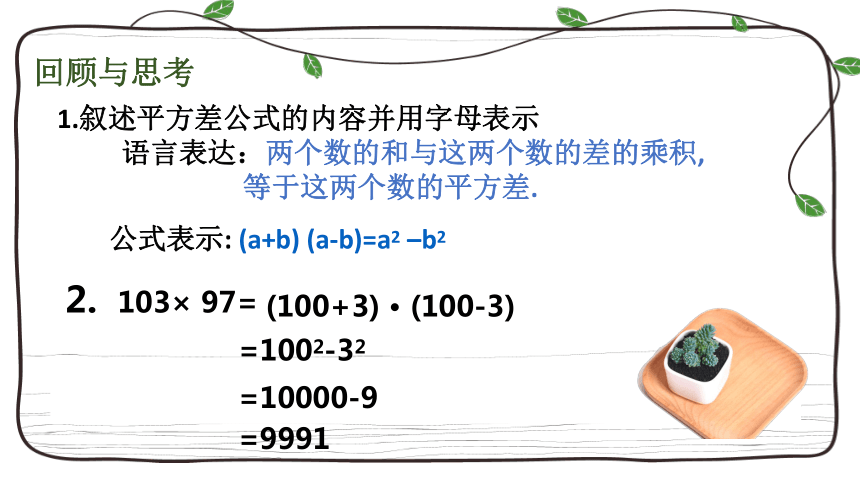
1.叙述平方差公式的内容并用字母表示
语言表达:两个数的和与这两个数的差的乘积,
等于这两个数的平方差.
公式表示: (a+b) (a-b)=a2 –b2
2. 103× 97=
(100+3) · (100-3)
=1002-32
=10000-9
=9991
回顾
平方差公式
(a+b)(a b)=a2 b2;
公式的结构特征:
左边是两个二项式的乘积,即两数和与这两数差的积。
右边是两数的平方差。
应用平方差公式的注意事项:
弄清在什么情况下才能使用平方差公式:
对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”;
仅当把两个二项式的积变成公式标准形式后,才能使用平方差公式。
在解题过程中要准确确定a和b对照公式原形的两边, 做到不弄错符号、当第一、二数是乘积且被平方时要注意添括号,是运用平方差公式进行多项式乘法的关键。
新课导入
图1
a
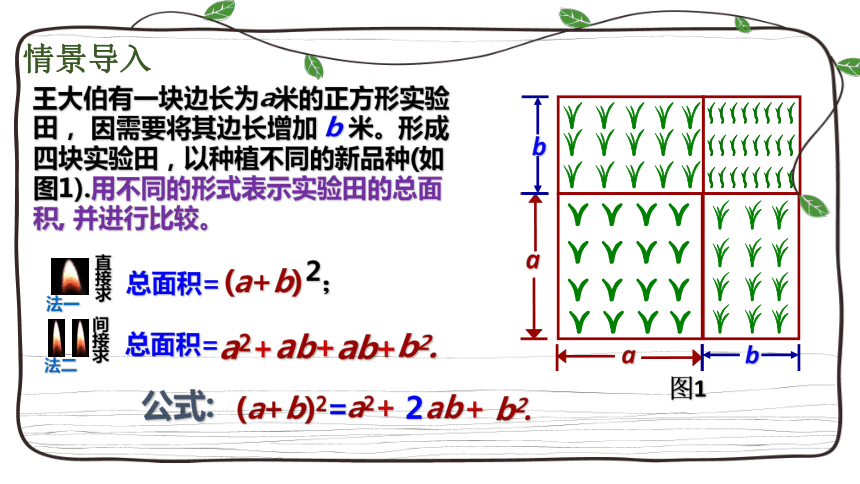
王大伯有一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块实验田,以种植不同的新品种(如图1).用不同的形式表示实验田的总面积, 并进行比较。
a
b
b
法一
直
接
求
总面积=
(a+b) ;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
公式:
情景导入
完全平方公式
几何证明
完全平方(和)公式的几何证明:
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式的应用
(1) (x+2y)
2
解:
⑴ ( x +2y) =
2
x
2
+ 2
·x
·2y
+ (2y)
2
+ 2
a
b
a
2
( a + b ) =
2
+ b
2
+ b
2
= x + 4xy + 4y
2 2
注意括号哦
x
a
2y
b
a
2
+ 2
a
b
分析:使用完全平方公式与平方差公式的使用一样,先把要
计算的式子与完全平方公式对照,明确个是a,哪个是b。
知识应用
解:=
=
(2)
解:
归纳
(a + b)
2
= a + 2ab + b
2 2
完全平方公(和)式的特点
(1)左边两数的和,右边是一个二次三项式,
其中有两项是公式左边二项式中的每一项的平方,
另一项是左边二项式中两项乘积的两倍。
(首平方尾平方,积的二倍放中央。)
(2)公式中的a,b可以表示任意的代数式。
(3)对于两数的和的平方,都可以用此公式。
思考
(1) 你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
推证
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(2)
a2 2ab+b2.
小颖写出了如下的算式:
(a b)2=
[a+( b)]2
(a b)2=
她是怎么想的
利用两数和的
完全平方公式
推证公式
(a b)2=
[a+( b)]2
你能继续做下去吗
= 2 +2 + 2
( b)
( b)
=
a2
2ab
b2.
+
a
a
几何证明
a
a
(a-b)
ab
ab
b
b
b
完全平方(差)公式的几何证明:
归纳
PPT模板:www./moban/ PPT素材:www./sucai/
PPT背景:www./beijing/ PPT图表:www./tubiao/
PPT下载:www./xiazai/ PPT教程: www./powerpoint/
资料下载:www./ziliao/ 范文下载:www./fanwen/
试卷下载:www./shiti/ 教案下载:www./jiaoan/
PPT论坛:www. PPT课件:www./kejian/
语文课件:www./kejian/yuwen/ 数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/ 美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/ 物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/ 生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/ 历史课件:www./kejian/lishi/
完全平方公式的结构特点:
①等号左边两个数的和(或差)的平方
②等号右边是等号左边两个数的平方和加上(或减去)这两个数的乘积的2倍
首平方,尾平方,
首尾2倍放中央,
中间符号同前方
知识应用
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
错
错
错
错
例2.完成填空x2+y2=(x+y)2- =(x- y)2+ .
【解析】解:由(x+y)2=x2+2xy+y2,
(x- y)2=x2- 2xy+y2
可知x2+y2=(x+y)2- 2xy=(x- y)2+2xy.
故两空格都填入2xy
例1.计算:(- 2x+1)2.
【解析】解:(- 2x+1)2
=(- 2x)2+2(- 2x)×1+12
=4x2- 4x+1.
例题讲练
2xy
2xy
例3.化简(x-3)2 - x(x-6)的结果为( ).
A.6x-9 B.-12x+9 C.9 D.3x+9
【答案】C
【解析】解:(x-3)2 - x(x-6)
=x2-2×3x+32-x2+6x
=x2-6x+9-x2+6x
=9
【点睛】考查完全平方公式,单项式乘多项式.
C
此处添加文本标题
Here to add your text, mainly to avoid large sections of text.Here to add your text.Here to add your text, mainly to avoid large sections of text.Here to add your text.
Here to add your text,
例4.下列运算正确的是 ( )
A.a3+a2=a5
B.(ab2)2=ab4
C.(a+b)(a- b)=a2- b2
D.(a+b)2=a2+b2
解:A选项中a3与a2不是同类项,不能合并,故A错误;
B选项(ab2)2=a2b4,故B错误;
C选项(a+b)(a- b)=a2- b2,故C正确;
D选项(a+b)2=a2+2ab+b2,故D错误. 故选C.
C
课堂总结
(1)两个公式的左边都是一个二项式的完全平方的形式:两者仅有一个“符号”不同
(2)两个公式的右边都是二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同
(3)公式中的字母a,b可以表示任意代数式。,b可以表示数,单项式和多项式。
课堂总结
1.完全平方公式的字母表示为:
2.完全平方公式的语言描述:
(a+b)2=a2+2ab+b2;
(a- b)2=a2- 2ab+b2.
两数和(或差)的平方,等于这两数的平方和加上(或减去)这两数积的两倍
3.完全平方公式的特点
谢谢!
课后作业
(1) 1042
=(100+4)2
=10816
(2) 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
=10000+800+16
+2×100×4
解:
解:
完全平方公式
01
学习目标
02
回顾与思考
03
新课导入
04
完全平方公式
目录
CONTENTS
05
课堂总结
学习目标
学习目标
一、学习目标
1.完全平方公式的推导及其应用.
2.完全平方公式的几何背景.
3.经历探索完全平方公式的过程,进一步发展符号感和推理能力,培养有条理的思考和表达能力.
二、学习重点
1.完全平方公式的推导过程、结构特点、语言表述、几何解释.
2.完全平方公式的应用.
回顾与思考
回顾与思考
1.叙述平方差公式的内容并用字母表示
语言表达:两个数的和与这两个数的差的乘积,
等于这两个数的平方差.
公式表示: (a+b) (a-b)=a2 –b2
2. 103× 97=
(100+3) · (100-3)
=1002-32
=10000-9
=9991
回顾
平方差公式
(a+b)(a b)=a2 b2;
公式的结构特征:
左边是两个二项式的乘积,即两数和与这两数差的积。
右边是两数的平方差。
应用平方差公式的注意事项:
弄清在什么情况下才能使用平方差公式:
对于一般两个二项式的积, 看准有无相等的“项”和符号相反的“项”;
仅当把两个二项式的积变成公式标准形式后,才能使用平方差公式。
在解题过程中要准确确定a和b对照公式原形的两边, 做到不弄错符号、当第一、二数是乘积且被平方时要注意添括号,是运用平方差公式进行多项式乘法的关键。
新课导入
图1
a
王大伯有一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。形成四块实验田,以种植不同的新品种(如图1).用不同的形式表示实验田的总面积, 并进行比较。
a
b
b
法一
直
接
求
总面积=
(a+b) ;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
公式:
情景导入
完全平方公式
几何证明
完全平方(和)公式的几何证明:
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方和公式的应用
(1) (x+2y)
2
解:
⑴ ( x +2y) =
2
x
2
+ 2
·x
·2y
+ (2y)
2
+ 2
a
b
a
2
( a + b ) =
2
+ b
2
+ b
2
= x + 4xy + 4y
2 2
注意括号哦
x
a
2y
b
a
2
+ 2
a
b
分析:使用完全平方公式与平方差公式的使用一样,先把要
计算的式子与完全平方公式对照,明确个是a,哪个是b。
知识应用
解:=
=
(2)
解:
归纳
(a + b)
2
= a + 2ab + b
2 2
完全平方公(和)式的特点
(1)左边两数的和,右边是一个二次三项式,
其中有两项是公式左边二项式中的每一项的平方,
另一项是左边二项式中两项乘积的两倍。
(首平方尾平方,积的二倍放中央。)
(2)公式中的a,b可以表示任意的代数式。
(3)对于两数的和的平方,都可以用此公式。
思考
(1) 你能用多项式的乘法法则来说明它成立吗
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
推证
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(2)
a2 2ab+b2.
小颖写出了如下的算式:
(a b)2=
[a+( b)]2
(a b)2=
她是怎么想的
利用两数和的
完全平方公式
推证公式
(a b)2=
[a+( b)]2
你能继续做下去吗
= 2 +2 + 2
( b)
( b)
=
a2
2ab
b2.
+
a
a
几何证明
a
a
(a-b)
ab
ab
b
b
b
完全平方(差)公式的几何证明:
归纳
PPT模板:www./moban/ PPT素材:www./sucai/
PPT背景:www./beijing/ PPT图表:www./tubiao/
PPT下载:www./xiazai/ PPT教程: www./powerpoint/
资料下载:www./ziliao/ 范文下载:www./fanwen/
试卷下载:www./shiti/ 教案下载:www./jiaoan/
PPT论坛:www. PPT课件:www./kejian/
语文课件:www./kejian/yuwen/ 数学课件:www./kejian/shuxue/
英语课件:www./kejian/yingyu/ 美术课件:www./kejian/meishu/
科学课件:www./kejian/kexue/ 物理课件:www./kejian/wuli/
化学课件:www./kejian/huaxue/ 生物课件:www./kejian/shengwu/
地理课件:www./kejian/dili/ 历史课件:www./kejian/lishi/
完全平方公式的结构特点:
①等号左边两个数的和(或差)的平方
②等号右边是等号左边两个数的平方和加上(或减去)这两个数的乘积的2倍
首平方,尾平方,
首尾2倍放中央,
中间符号同前方
知识应用
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
错
错
错
错
例2.完成填空x2+y2=(x+y)2- =(x- y)2+ .
【解析】解:由(x+y)2=x2+2xy+y2,
(x- y)2=x2- 2xy+y2
可知x2+y2=(x+y)2- 2xy=(x- y)2+2xy.
故两空格都填入2xy
例1.计算:(- 2x+1)2.
【解析】解:(- 2x+1)2
=(- 2x)2+2(- 2x)×1+12
=4x2- 4x+1.
例题讲练
2xy
2xy
例3.化简(x-3)2 - x(x-6)的结果为( ).
A.6x-9 B.-12x+9 C.9 D.3x+9
【答案】C
【解析】解:(x-3)2 - x(x-6)
=x2-2×3x+32-x2+6x
=x2-6x+9-x2+6x
=9
【点睛】考查完全平方公式,单项式乘多项式.
C
此处添加文本标题
Here to add your text, mainly to avoid large sections of text.Here to add your text.Here to add your text, mainly to avoid large sections of text.Here to add your text.
Here to add your text,
例4.下列运算正确的是 ( )
A.a3+a2=a5
B.(ab2)2=ab4
C.(a+b)(a- b)=a2- b2
D.(a+b)2=a2+b2
解:A选项中a3与a2不是同类项,不能合并,故A错误;
B选项(ab2)2=a2b4,故B错误;
C选项(a+b)(a- b)=a2- b2,故C正确;
D选项(a+b)2=a2+2ab+b2,故D错误. 故选C.
C
课堂总结
(1)两个公式的左边都是一个二项式的完全平方的形式:两者仅有一个“符号”不同
(2)两个公式的右边都是二次三项式,其中有两项是公式左边二项式中每一项的平方,中间一项是左边二项式中两项乘积的2倍,两者也仅有一个“符号”不同
(3)公式中的字母a,b可以表示任意代数式。,b可以表示数,单项式和多项式。
课堂总结
1.完全平方公式的字母表示为:
2.完全平方公式的语言描述:
(a+b)2=a2+2ab+b2;
(a- b)2=a2- 2ab+b2.
两数和(或差)的平方,等于这两数的平方和加上(或减去)这两数积的两倍
3.完全平方公式的特点
谢谢!
课后作业
(1) 1042
=(100+4)2
=10816
(2) 99.992
= (100 –0.01)2
=10000 -2+0.0001
=9998.0001
=10000+800+16
+2×100×4
解:
解:
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
