人教版数学八年级上册 12.2 第3课时 三角形全等的判定(三)(ASA,AAS)课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2 第3课时 三角形全等的判定(三)(ASA,AAS)课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 490.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-09 12:46:22 | ||
图片预览



文档简介
(共21张PPT)
12.2 三角形全等的判定
第3课时 三角形全等的判定(三)(ASA,AAS)
学习目标
1.探索并正确理解“ASA”和“AAS”判定方法.
2.会用“ASA”和“AAS”判定方法证明两个三角形全等.
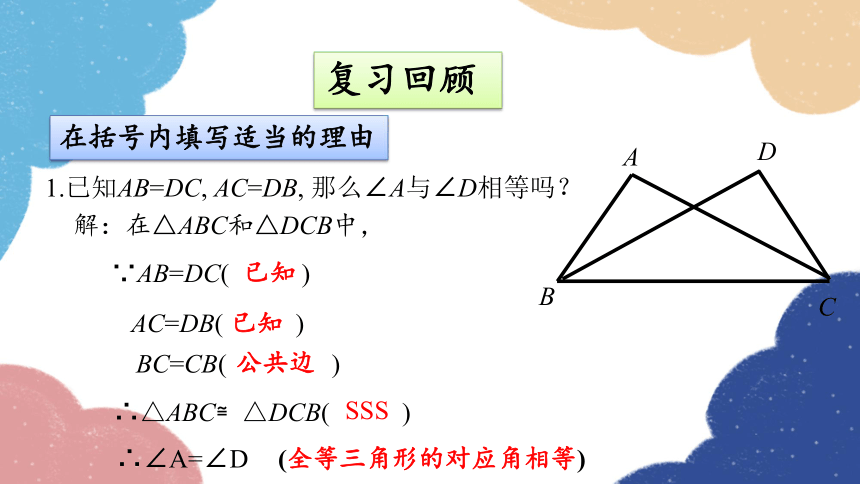
1.已知AB=DC, AC=DB, 那么∠A与∠D相等吗?
∵AB=DC( )
AC=DB( )
BC=CB( )
∴△ABC≌△DCB( )
∴∠A=∠D
A
B
C
D
已知
已知
公共边
SSS
(全等三角形的对应角相等)
解:在△ABC和△DCB中,
复习回顾
在括号内填写适当的理由
2.已知:如图,AB =AC ,AD = AE .求证:△ ABE≌ △ ACD.
证明: 在△ABE 和△ACD 中,
AB = AC( ),
AE = AD( ).
∠A = ∠A( ),
∴ △ ABE ≌ △ ACD(SAS).
B
E
A
C
D
复习回顾
已知
公共角
已知
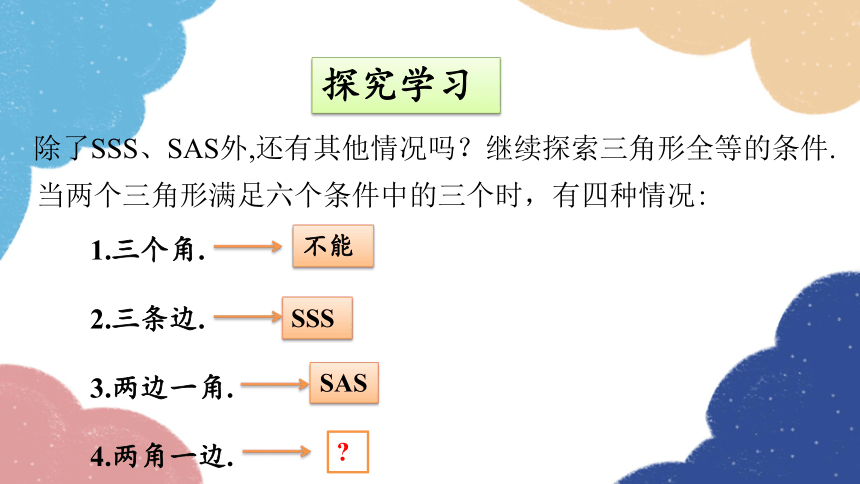
除了SSS、SAS外,还有其他情况吗?继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能
SAS
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
探究学习
A
B
C
A
B
C
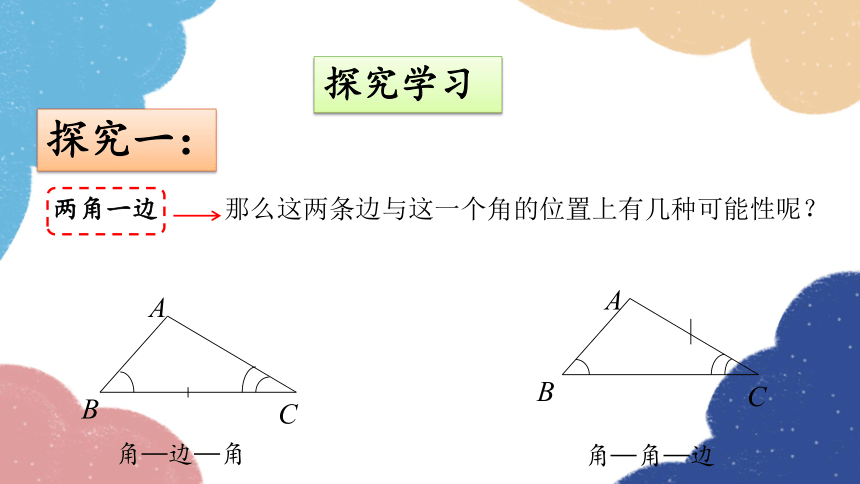
探究学习
探究一:
两角一边 那么这两条边与这一个角的位置上有几种可能性呢?
角—边—角
角—角—边
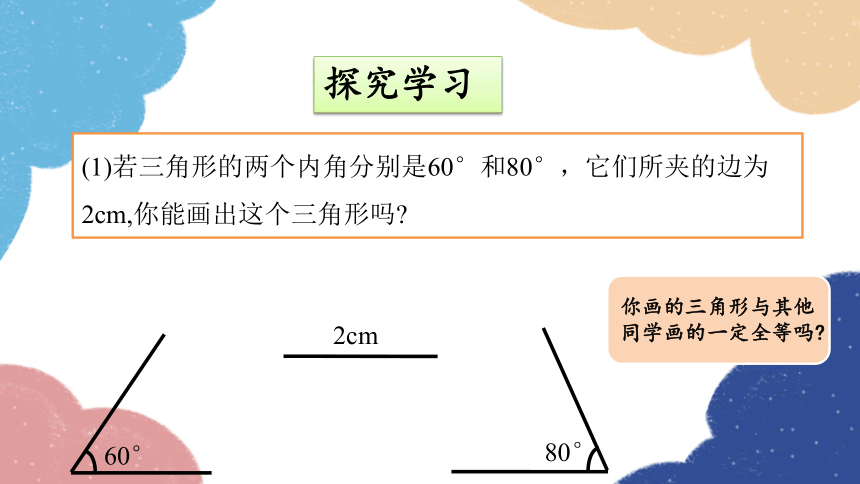
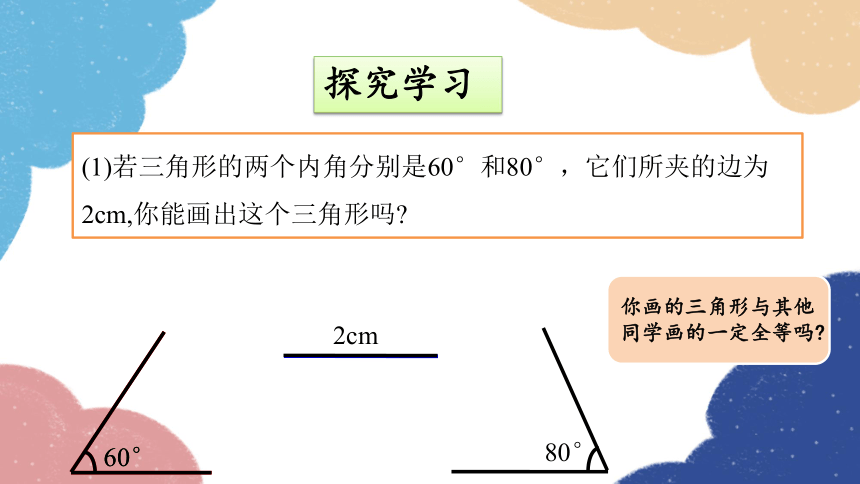
(1)若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
探究学习
2cm
60°
80°
你画的三角形与其他同学画的一定全等吗
80°
(1)若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
探究学习
2cm
60°
60°
你画的三角形与其他同学画的一定全等吗
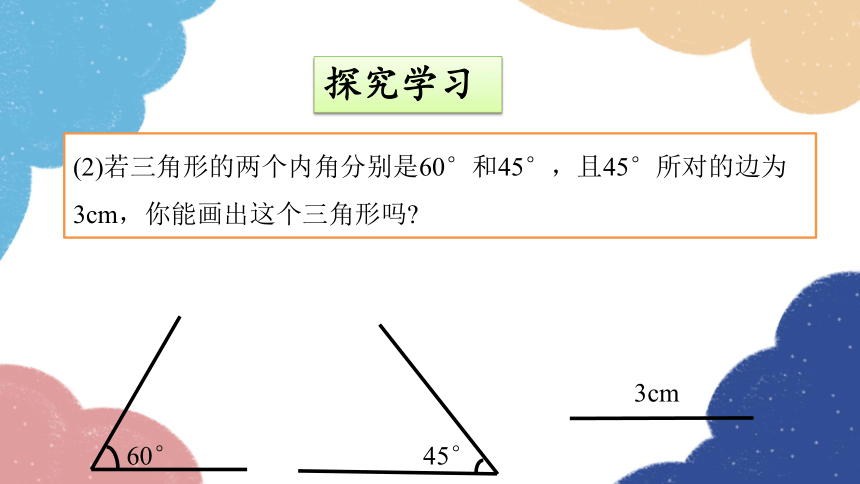
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
60°
45°
3cm
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
这里的条件与(1)中的条件有什么相同点与不同点?你能将它转化为(1)中的条件吗?
45°
45°
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
60°
45°
3cm
两角和它们的夹边对应相等的两个
三角形全等 . 简写成“角边角”或“ASA”.
探究反映的规律(一) :
知识讲解
角边角公理
D
C
A′
E
B
A
∠A=∠A′ (已知 )
AB=A′C (已知 )
∠B=∠C (已知 )
在△ABE和△A′CD中
∴ △ABE≌△A′CD (ASA)
知识讲解
符号语言
知识讲解
探究反映的规律(二) :
角角边公理
两个角和其中一个角的对边对应相等的两个三角形全等. 简写成“角角边”或“AAS”.
D
C
A′
E
B
A
AE=A′D(已知 )
∠A=∠A′ (已知 )
∠B=∠C(已知 )
在△ABE和△A′CD中
∴ △ABE≌△A′CD(AAS)
知识讲解
符号语言
典例
例1:如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
分析:由∠BAC=∠DAE得∠BAC-∠CAE=∠DAE-∠CAE,
即得∠BAE=∠CAD,然后利用“角边角”证全等.
典例
例1:如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
∠BAE=∠CAD,
AB=AC,
∠ABE=∠ACD.
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(ASA).
典例
例2 如图,已知∠1 = ∠2,∠C = ∠D.
求证:AC = AD.
A
B
D
C
2
1
证明:在△ABC和△ABD中
∠1 = ∠2
∠C = ∠D
AB = AB
∴△ABC≌△ABD( )
∴AC = AD(全等三角形对应边相等)
AAS
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中和△ABC全等的图形是( ).
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:甲图只有两个已知元素,不能确定与△ABC是否全等;乙图与△ABC满足“SAS”的条件,所以两个图形全等;丙图与△ABC满足“AAS”的条件,所以两个图形也全等.故答案是B.
随堂训练
B
2.如图所示,AB∥CD,AF∥DE,BE=CF.
求证:AB=CD.
随堂训练
证明:∵AB∥CD,∴∠B=∠C.
∵AF∥DE, ∴∠AFB=∠DEC.
∵BE=CF, ∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE.
∴AB=CD.
课时小结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
1.边边边 (SSS)
3.角边角 (ASA)
4.角角边 (AAS)
2.边角边 (SAS)
12.2 三角形全等的判定
第3课时 三角形全等的判定(三)(ASA,AAS)
学习目标
1.探索并正确理解“ASA”和“AAS”判定方法.
2.会用“ASA”和“AAS”判定方法证明两个三角形全等.
1.已知AB=DC, AC=DB, 那么∠A与∠D相等吗?
∵AB=DC( )
AC=DB( )
BC=CB( )
∴△ABC≌△DCB( )
∴∠A=∠D
A
B
C
D
已知
已知
公共边
SSS
(全等三角形的对应角相等)
解:在△ABC和△DCB中,
复习回顾
在括号内填写适当的理由
2.已知:如图,AB =AC ,AD = AE .求证:△ ABE≌ △ ACD.
证明: 在△ABE 和△ACD 中,
AB = AC( ),
AE = AD( ).
∠A = ∠A( ),
∴ △ ABE ≌ △ ACD(SAS).
B
E
A
C
D
复习回顾
已知
公共角
已知
除了SSS、SAS外,还有其他情况吗?继续探索三角形全等的条件.
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能
SAS
1.三个角.
2.三条边.
3.两边一角.
4.两角一边.
探究学习
A
B
C
A
B
C
探究学习
探究一:
两角一边 那么这两条边与这一个角的位置上有几种可能性呢?
角—边—角
角—角—边
(1)若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
探究学习
2cm
60°
80°
你画的三角形与其他同学画的一定全等吗
80°
(1)若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
探究学习
2cm
60°
60°
你画的三角形与其他同学画的一定全等吗
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
60°
45°
3cm
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
这里的条件与(1)中的条件有什么相同点与不同点?你能将它转化为(1)中的条件吗?
45°
45°
(2)若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗
探究学习
60°
45°
3cm
两角和它们的夹边对应相等的两个
三角形全等 . 简写成“角边角”或“ASA”.
探究反映的规律(一) :
知识讲解
角边角公理
D
C
A′
E
B
A
∠A=∠A′ (已知 )
AB=A′C (已知 )
∠B=∠C (已知 )
在△ABE和△A′CD中
∴ △ABE≌△A′CD (ASA)
知识讲解
符号语言
知识讲解
探究反映的规律(二) :
角角边公理
两个角和其中一个角的对边对应相等的两个三角形全等. 简写成“角角边”或“AAS”.
D
C
A′
E
B
A
AE=A′D(已知 )
∠A=∠A′ (已知 )
∠B=∠C(已知 )
在△ABE和△A′CD中
∴ △ABE≌△A′CD(AAS)
知识讲解
符号语言
典例
例1:如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
分析:由∠BAC=∠DAE得∠BAC-∠CAE=∠DAE-∠CAE,
即得∠BAE=∠CAD,然后利用“角边角”证全等.
典例
例1:如图,AB=AC,∠ABE=∠ACD,∠BAC=∠DAE.
求证:△ABE≌△ACD.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠CAE=∠DAE-∠CAE,
∠BAE=∠CAD,
AB=AC,
∠ABE=∠ACD.
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(ASA).
典例
例2 如图,已知∠1 = ∠2,∠C = ∠D.
求证:AC = AD.
A
B
D
C
2
1
证明:在△ABC和△ABD中
∠1 = ∠2
∠C = ∠D
AB = AB
∴△ABC≌△ABD( )
∴AC = AD(全等三角形对应边相等)
AAS
1.已知△ABC的六个元素如图所示,则甲、乙、丙三个三角形中和△ABC全等的图形是( ).
A.甲、乙 B.乙、丙 C.只有乙 D.只有丙
解析:甲图只有两个已知元素,不能确定与△ABC是否全等;乙图与△ABC满足“SAS”的条件,所以两个图形全等;丙图与△ABC满足“AAS”的条件,所以两个图形也全等.故答案是B.
随堂训练
B
2.如图所示,AB∥CD,AF∥DE,BE=CF.
求证:AB=CD.
随堂训练
证明:∵AB∥CD,∴∠B=∠C.
∵AF∥DE, ∴∠AFB=∠DEC.
∵BE=CF, ∴BE+EF=CF+EF,即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE.
∴AB=CD.
课时小结
到目前为止,我们一共探索出判定三角形全等的四种规律,它们分别是:
1.边边边 (SSS)
3.角边角 (ASA)
4.角角边 (AAS)
2.边角边 (SAS)
