勾股定理的应用
图片预览

文档简介
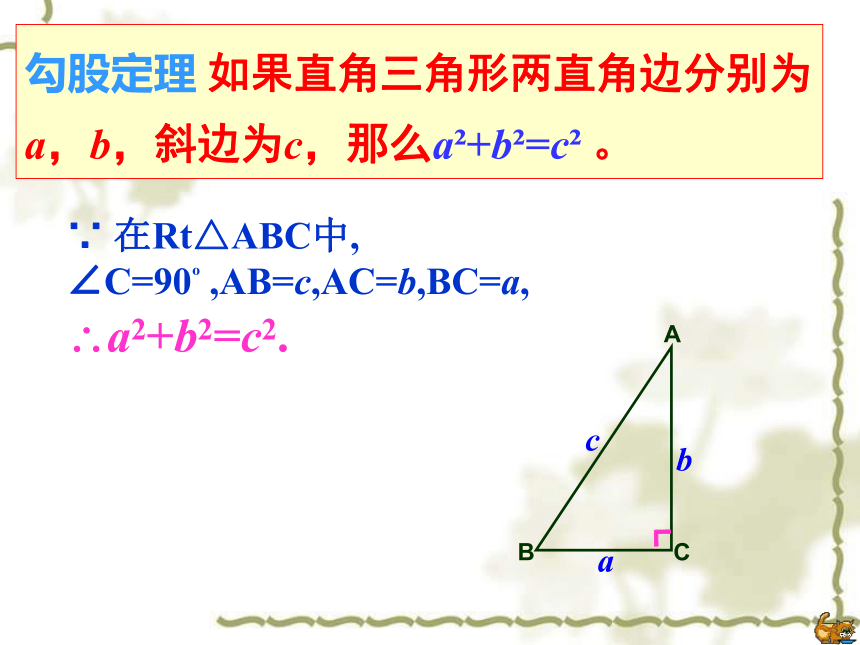
课件28张PPT。14.2勾股定理的应用(三)勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2 。∵ 在Rt△ABC中, ∠C=90o ,AB=c,AC=b,BC=a,
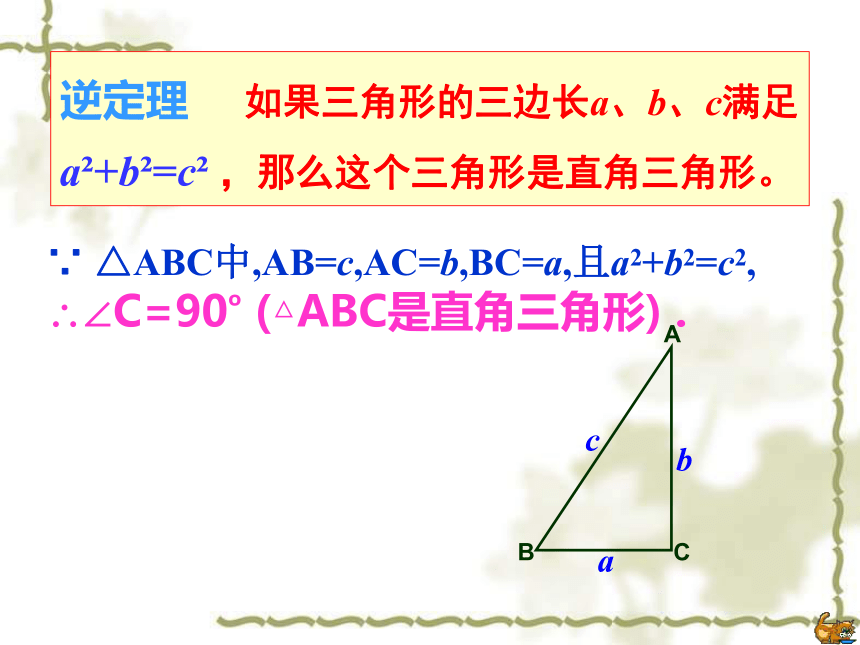
?a2+b2=c2.┏逆定理 如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。∵ △ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
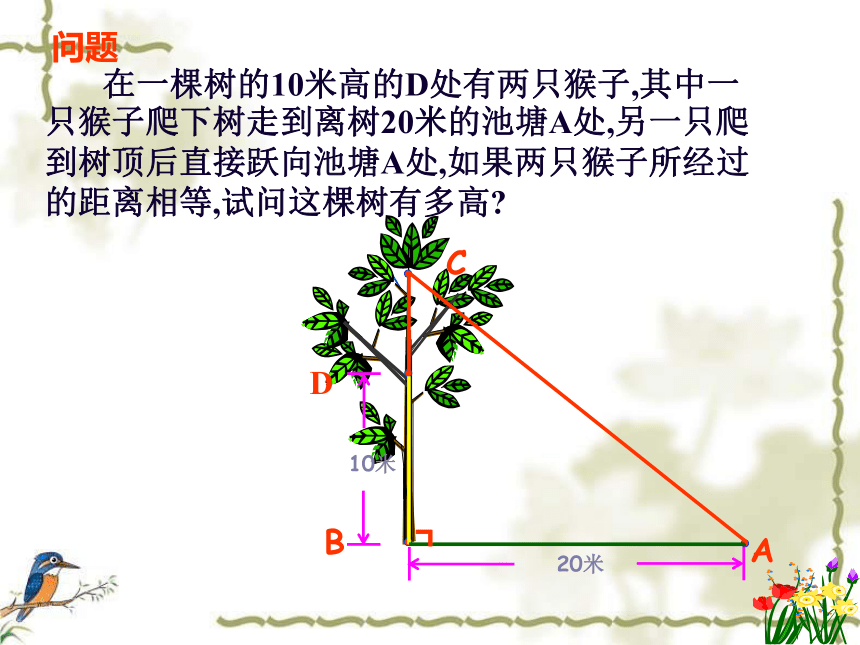
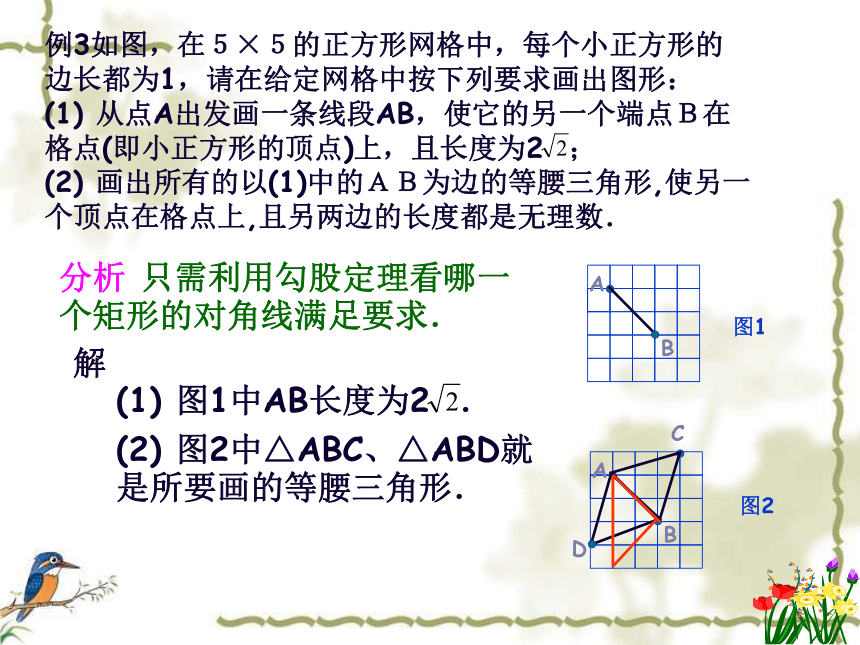
?∠C=90o (△ABC是直角三角形) . 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的距离相等,试问这棵树有多高?ABC10米20米┏问题D例3如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:
(1) 从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为2 ;
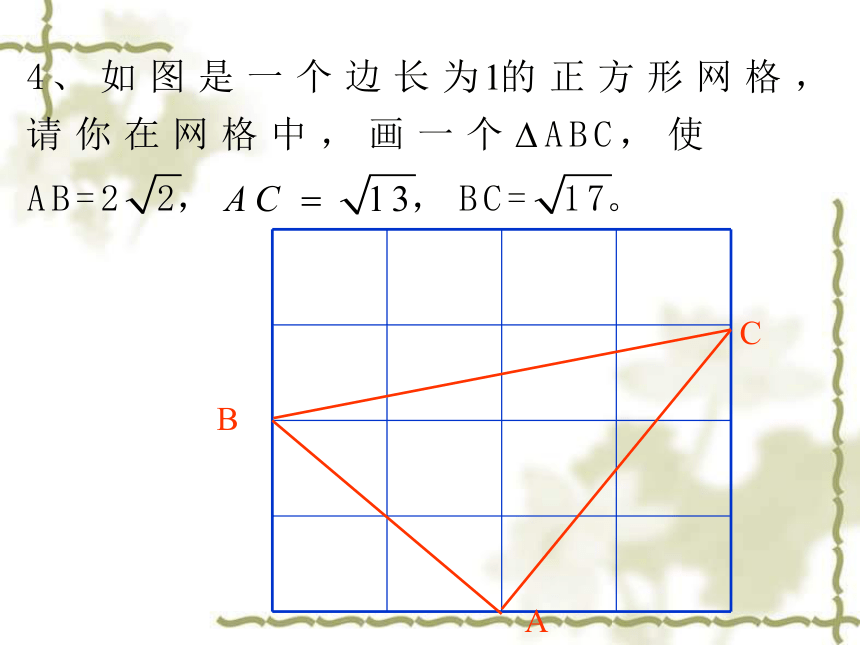
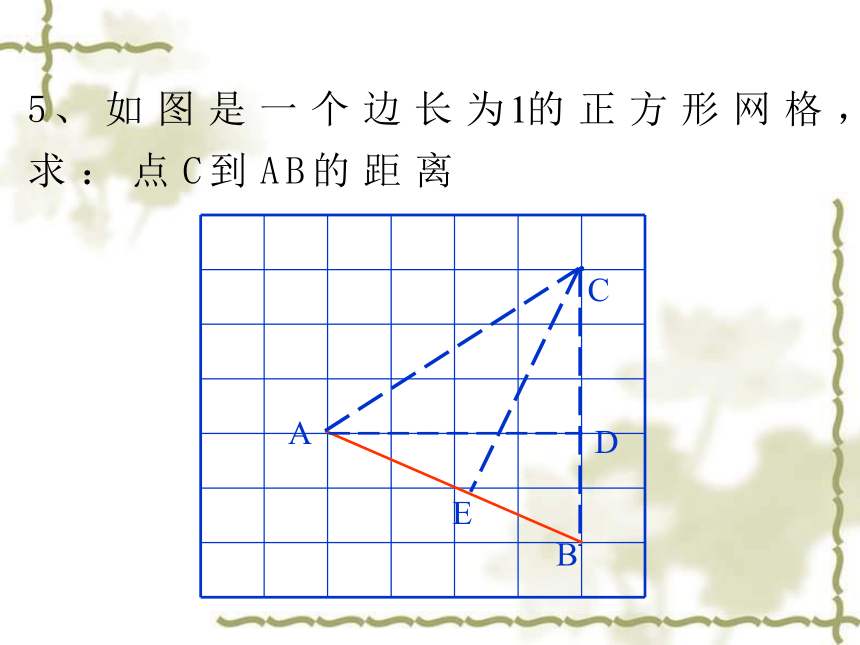
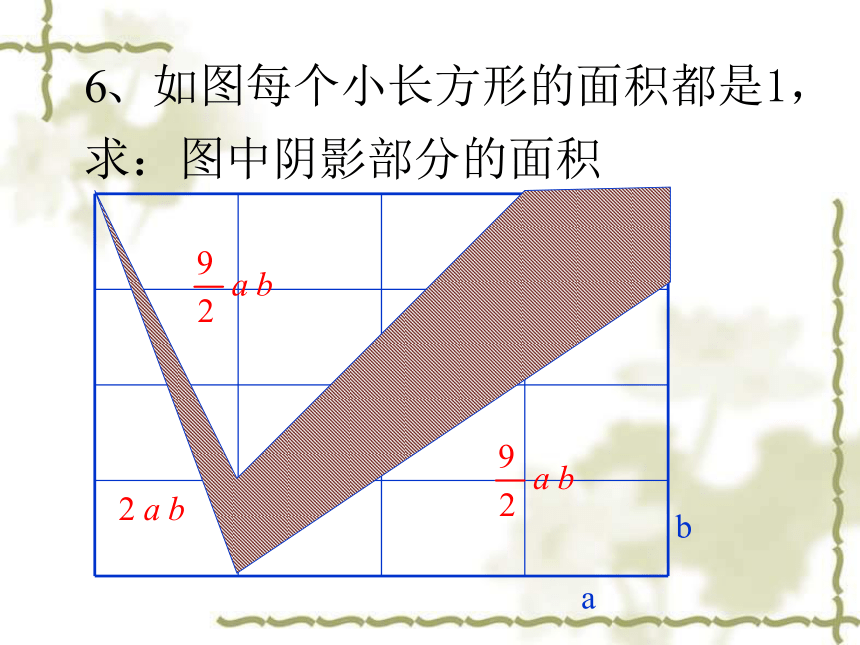
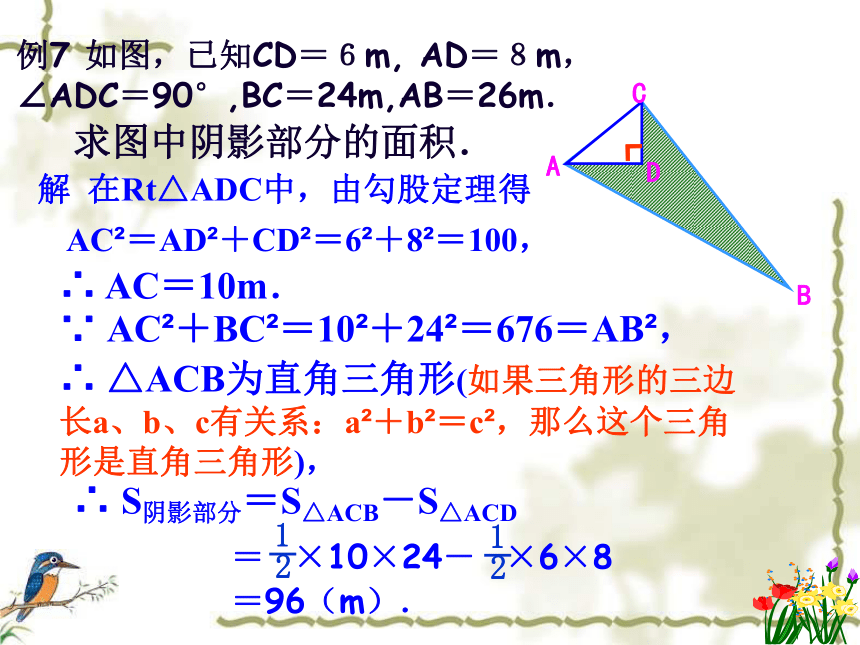
(2) 画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且另两边的长度都是无理数.A分析 只需利用勾股定理看哪一个矩形的对角线满足要求.解 (1) 图1中AB长度为2 .(2) 图2中△ABC、△ABD就是所要画的等腰三角形.图1图2CBDABC●DEab例7 如图,已知CD=6m, AD=8m, ∠ADC=90°,BC=24m,AB=26m. 解 在Rt△ADC中,由勾股定理得AC2=AD2+CD2=62+82=100,∴ AC=10m.∵ AC2+BC2=102+242=676=AB2,∴ △ACB为直角三角形(如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形),∴ S阴影部分=S△ACB-S△ACD求图中阴影部分的面积.= ×10×24- ×6×8=96(m).┏CEGHM10.在一块宽AN=5cm,长ND=10cm的砖块的棱CD上有一点B距底面BD=8cm,砖块下底面A点处有一只蜗牛想爬到B处,需要爬行的最短路径是多少?ED4m5m11、如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,那么至少要买地毯多少米?4m5m12、如图所示,为了测出电视塔到学校的距离,小明把手表的12点指向正北,此时学校在2点所指的方向,电视塔在11点所指的方向,水塔在正东方向,且位于学校正南,已知小明距水塔2000 米,电视塔距小明3000米,小明距学校的距离是学校距水塔的2倍,那么电视塔距学校多远呢?┏┏ABCD13、一架长为10m的梯子AB斜靠在墙上.⑴ 若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远?ABC⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m?⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗?◆一架长为10m的梯子AB斜靠在墙上.ABC⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗?DEE
?a2+b2=c2.┏逆定理 如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。∵ △ABC中,AB=c,AC=b,BC=a,且a2+b2=c2,
?∠C=90o (△ABC是直角三角形) . 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的距离相等,试问这棵树有多高?ABC10米20米┏问题D例3如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:
(1) 从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为2 ;
(2) 画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且另两边的长度都是无理数.A分析 只需利用勾股定理看哪一个矩形的对角线满足要求.解 (1) 图1中AB长度为2 .(2) 图2中△ABC、△ABD就是所要画的等腰三角形.图1图2CBDABC●DEab例7 如图,已知CD=6m, AD=8m, ∠ADC=90°,BC=24m,AB=26m. 解 在Rt△ADC中,由勾股定理得AC2=AD2+CD2=62+82=100,∴ AC=10m.∵ AC2+BC2=102+242=676=AB2,∴ △ACB为直角三角形(如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形),∴ S阴影部分=S△ACB-S△ACD求图中阴影部分的面积.= ×10×24- ×6×8=96(m).┏CEGHM10.在一块宽AN=5cm,长ND=10cm的砖块的棱CD上有一点B距底面BD=8cm,砖块下底面A点处有一只蜗牛想爬到B处,需要爬行的最短路径是多少?ED4m5m11、如图是6级台阶侧面的示意图,如果要在台阶上铺地毯,那么至少要买地毯多少米?4m5m12、如图所示,为了测出电视塔到学校的距离,小明把手表的12点指向正北,此时学校在2点所指的方向,电视塔在11点所指的方向,水塔在正东方向,且位于学校正南,已知小明距水塔2000 米,电视塔距小明3000米,小明距学校的距离是学校距水塔的2倍,那么电视塔距学校多远呢?┏┏ABCD13、一架长为10m的梯子AB斜靠在墙上.⑴ 若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远?ABC⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m?⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗?◆一架长为10m的梯子AB斜靠在墙上.ABC⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗?DEE
