鲁教版(五四学制)六年级下册5.5多边形与圆 课件(共33张PPT)
文档属性
| 名称 | 鲁教版(五四学制)六年级下册5.5多边形与圆 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 760.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-10 18:17:32 | ||
图片预览









文档简介
(共33张PPT)
多边形与圆
2023
01
02
03
04
学习
目标
多边形
圆
当堂
检测
目录
05
课堂
总结
学习目标
第1章
1、强化多边形的对角线、内角和公式、外角和定理的计算(重难点)
2、强化对圆的概念、圆的周长、圆的面积问题(重点)
学习目标
3、进一步熟悉和掌握数形结合思想、方程思想、整体思想、转化思想及分类讨论思想等解题方法及技巧
多边形
第2章
多边形的概念
多边形 定义 面内,若干条线段_____________,且有公共端点的线段 ,这样得到的图形叫做多边形.
边 组成多边形的各条_____,
如果一个多边形有n条边,就叫做______.
顶点 多边形边的_________.
角 多边形___________所组成的角叫做多边形的内角,简称多边形的角.
对角线 连接多边形_______的两个顶点的线段.
首尾顺次相接
不在同一条直线上
线段
n边形
公共端点
相邻两条边
不相邻
正多边形:各边相等,各角也相等的多边形.
1.判断对错:
(1)一个多边形有几条边,就有几个角. ( )
(2)过六边形的每一个顶点都可以作2条对角线. ( )
(3)各边都相等的多边形是正多边形. ( )
(4)一个多边形的内角不能都是直角. ( )
跟踪练习
√
×
×
×
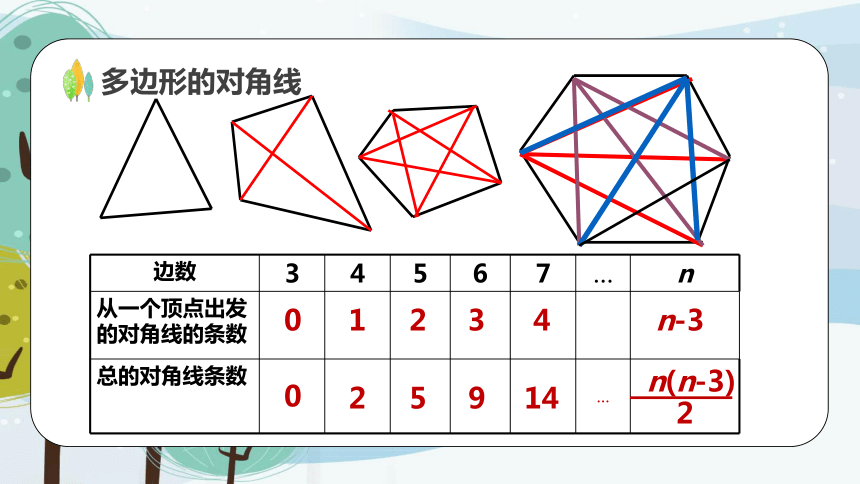
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
总的对角线条数 …
0
0
1
2
2
5
3
9
4
14
n-3
n(n-3)
2
多边形的对角线
2、从n边形的一个顶点最多可引出5条对角线,则这是 边形,它共有 条对角线.
3、要使一个五边形具有稳定性,则需至少添加几条对角线. ( )
A.1
B.2
C.3
D.4
八
B
跟踪练习
20
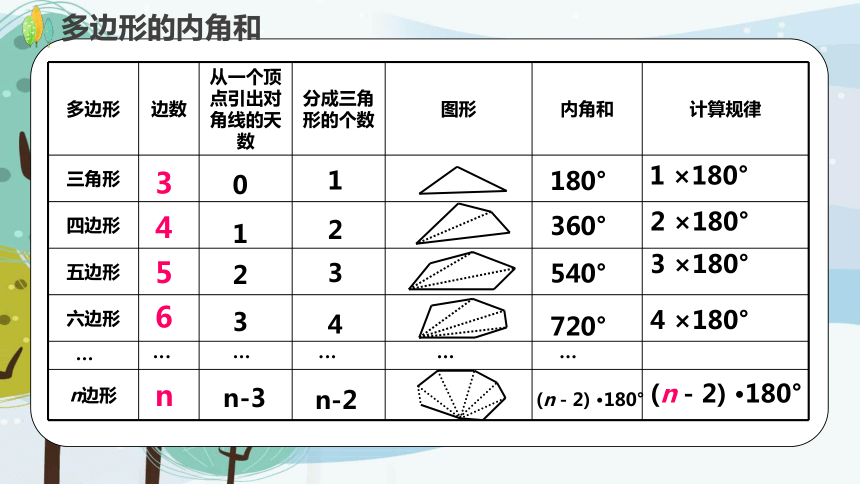
多边形 边数 从一个顶点引出对角线的天数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
n边形
3
4
5
6
n
n-2
1
2
3
4
180°
360°
540°
720°
(n-2) ·180°
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n-3
0
1
3
2
...
...
...
...
...
...
多边形的内角和
n边形的外角和等于 ;
360°
■注意:
1. n边形的外角和是个定值(不随边数的变化而变化);
多边形的外角和
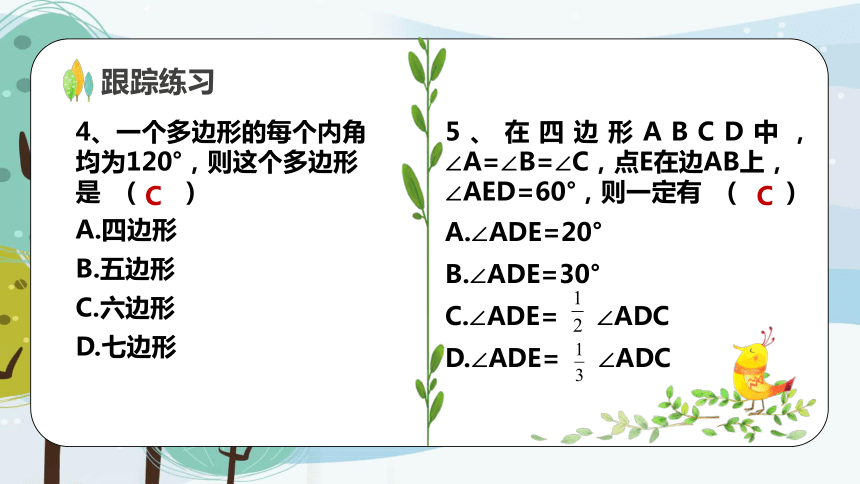
4、一个多边形的每个内角均为120°,则这个多边形是 ( )
A.四边形
B.五边形
C.六边形
D.七边形
5、在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,
∠AED=60°,则一定有 ( )
A.∠ADE=20°
B.∠ADE=30°
C.∠ADE= ∠ADC
D.∠ADE= ∠ADC
C
C
跟踪练习
6、一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
7、若一个多边形的每个内角都108°是,则这个多边形的内角和为( )
A.360°
B.540°
C.720°
D.900°
B
B
跟踪练习
密铺的条件:密铺时不仅要考虑公共顶点处要拼成一个周角,还要使公共边相等。
正多边形的密铺有三个限制条件
①边长相等
②顶点公共
③在一个顶点处各个正多边形的内角之和为360°
同一种正多边形能密铺地面的只有三种:正三角形、正方形、正六边形.
多边形的密铺
8、下列形状的地砖中,不能把地面作既无缝隙又不重叠覆盖的地砖是( )
A.正三角形
B.正方形
C.正五边形
D.长方形
9、若一个多边形的对角线共有14条,则这个多边形的边数是( )
A.6
B.7
C.10
D.14
C
B
跟踪练习
圆
第3章
定义 圆是到定点的距离等于定长的点的集合,这个定点叫做 ,这个定长叫做 .圆心确定圆的 ,半径确定圆的 .
周长
面积
点与圆的位置关系 点在圆上 d r
点在圆内 d r
点在圆外 d r
圆心
半径
位置
大小
=
<
>
2πr
πr2
圆
10、点P到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是 ( )
A.5cm或11cm
B.2.5cm
C.5.5cm
D.2.5cm或5.5cm
11、Rt△ABC中,∠C=90°,CD⊥AB,AC=2,BC=3,若以C为圆心,以2为半径作☉C,则点A在☉C ,点B在☉C ,点D在☉C .
D
跟踪练习
上
外
内
弧 圆上任意两点间的部分叫做弧;圆上任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做 ,大于半圆的弧叫做 .
弦 连接圆上任意两点间的线段叫做弦;
过圆心的弦叫做 .
扇形 一条弧和经过这条弧的端点的两条半径所组成的图形
等圆 能够 的圆叫等圆
同心圆 圆心 ,半径 的圆叫做同心圆
劣弧
优弧
直径
相同
不同
重合
直径是圆中最长的弦.
表示优弧时,为了区别于劣弧,要用三个大写字母表示.
圆
12、如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )A.35°
B.40°
C.60°
D.70°
B
跟踪练习
13、下列说法中正确的个数为 ( )
①同圆中,直径的长等于半径长的2倍;
②过圆心的弦是直径;
③优弧大于劣弧.
A.0 B.1
C.2 D.3
C
当堂检测
第4章
2、已知一个正多边形的每个外角等于60°,则这个正多边形是 ( )
A.正五边形
B.正六边形
C.正七边形
D.正八边形
1、将一个n边形变成n+1边形,内角和将 ( )
A.减少180°
B.增加90°
C.增加180°
D.增加360°
C
C
当堂检测
4、如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来多边形的边数是 ( )
A.5
B.6
C.7
D.8
3、有两个正多边形,这两个正多边形的边数之比为1∶2,内角和之比为3∶8,则这两个多边形的边数各是 ( )
A.4,8
B.5,10
C.6,12
D.7,14
A
C
当堂检测
5、下列说法错误的是( )
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.能完全重合的两条弧是等弧
B
6、在一个三角形中,已知AB=AC=6cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为5cm的圆,则下列说法正确的是 ( )
A.点A在☉D外
B.点B在☉D上
C.点C在☉D内
D.无法确定
C
当堂检测
7、如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. -180°
B.180°-
C.
D.360°-
A
8、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.5
B.6
C.7
D.8
D
当堂检测
9、如图,∠1、∠2、∠3、∠4是五边形ABCDE的四个外角, 若∠A=120°,则∠1+∠2+∠3+∠4的度数为 .
300°
10、如图,正方形的边长为4,则图中阴影部分的面积为 . .
16-4π
当堂检测
当堂检测
11、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
当堂检测
解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,所以∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
∴∠BAF=150°,∠CDE=∠BAF=150°.
又∵六边形ABCDEF的内角和为(6-2)×180°=720°,
∴∠F=720°-∠B-∠C-∠CDE-∠E-∠BAF=130°
当堂检测
12、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
当堂检测
解:在四边形MCDH中, ∠1+∠C+∠D+∠DHM=360°,
∵∠1=∠A+∠B,
∴∠A+∠B+∠C+∠D=360°-∠DHM,
在四边形EFGH中,∠E+∠F+∠G=360°-∠GHE,
∴∠A+∠B+∠C+∠D+∠E+
∠F+∠G=360°-∠DHM+360°-∠GHE
=360°×2-(∠DHM+∠GHE)
=360°×2-180°=540°
课堂总结
第5章
多边形、正多边形的有关概念及表示
多边形的内、外角和、角平分线计算公式
多边形的密铺
圆的概念、周长面积公式、点与圆的位置关系
弧、等、等圆、同心圆的概念
多边形
圆
多边形与圆
课堂总结
THANK YOU!
2023
多边形与圆
2023
01
02
03
04
学习
目标
多边形
圆
当堂
检测
目录
05
课堂
总结
学习目标
第1章
1、强化多边形的对角线、内角和公式、外角和定理的计算(重难点)
2、强化对圆的概念、圆的周长、圆的面积问题(重点)
学习目标
3、进一步熟悉和掌握数形结合思想、方程思想、整体思想、转化思想及分类讨论思想等解题方法及技巧
多边形
第2章
多边形的概念
多边形 定义 面内,若干条线段_____________,且有公共端点的线段 ,这样得到的图形叫做多边形.
边 组成多边形的各条_____,
如果一个多边形有n条边,就叫做______.
顶点 多边形边的_________.
角 多边形___________所组成的角叫做多边形的内角,简称多边形的角.
对角线 连接多边形_______的两个顶点的线段.
首尾顺次相接
不在同一条直线上
线段
n边形
公共端点
相邻两条边
不相邻
正多边形:各边相等,各角也相等的多边形.
1.判断对错:
(1)一个多边形有几条边,就有几个角. ( )
(2)过六边形的每一个顶点都可以作2条对角线. ( )
(3)各边都相等的多边形是正多边形. ( )
(4)一个多边形的内角不能都是直角. ( )
跟踪练习
√
×
×
×
边数 3 4 5 6 7 … n
从一个顶点出发的对角线的条数
总的对角线条数 …
0
0
1
2
2
5
3
9
4
14
n-3
n(n-3)
2
多边形的对角线
2、从n边形的一个顶点最多可引出5条对角线,则这是 边形,它共有 条对角线.
3、要使一个五边形具有稳定性,则需至少添加几条对角线. ( )
A.1
B.2
C.3
D.4
八
B
跟踪练习
20
多边形 边数 从一个顶点引出对角线的天数 分成三角形的个数 图形 内角和 计算规律
三角形
四边形
五边形
六边形
n边形
3
4
5
6
n
n-2
1
2
3
4
180°
360°
540°
720°
(n-2) ·180°
(n-2) ·180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
n-3
0
1
3
2
...
...
...
...
...
...
多边形的内角和
n边形的外角和等于 ;
360°
■注意:
1. n边形的外角和是个定值(不随边数的变化而变化);
多边形的外角和
4、一个多边形的每个内角均为120°,则这个多边形是 ( )
A.四边形
B.五边形
C.六边形
D.七边形
5、在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,
∠AED=60°,则一定有 ( )
A.∠ADE=20°
B.∠ADE=30°
C.∠ADE= ∠ADC
D.∠ADE= ∠ADC
C
C
跟踪练习
6、一个多边形的外角和与它的内角和相等,则多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
7、若一个多边形的每个内角都108°是,则这个多边形的内角和为( )
A.360°
B.540°
C.720°
D.900°
B
B
跟踪练习
密铺的条件:密铺时不仅要考虑公共顶点处要拼成一个周角,还要使公共边相等。
正多边形的密铺有三个限制条件
①边长相等
②顶点公共
③在一个顶点处各个正多边形的内角之和为360°
同一种正多边形能密铺地面的只有三种:正三角形、正方形、正六边形.
多边形的密铺
8、下列形状的地砖中,不能把地面作既无缝隙又不重叠覆盖的地砖是( )
A.正三角形
B.正方形
C.正五边形
D.长方形
9、若一个多边形的对角线共有14条,则这个多边形的边数是( )
A.6
B.7
C.10
D.14
C
B
跟踪练习
圆
第3章
定义 圆是到定点的距离等于定长的点的集合,这个定点叫做 ,这个定长叫做 .圆心确定圆的 ,半径确定圆的 .
周长
面积
点与圆的位置关系 点在圆上 d r
点在圆内 d r
点在圆外 d r
圆心
半径
位置
大小
=
<
>
2πr
πr2
圆
10、点P到圆的最小距离为3cm,最大距离为8cm,则该圆的半径是 ( )
A.5cm或11cm
B.2.5cm
C.5.5cm
D.2.5cm或5.5cm
11、Rt△ABC中,∠C=90°,CD⊥AB,AC=2,BC=3,若以C为圆心,以2为半径作☉C,则点A在☉C ,点B在☉C ,点D在☉C .
D
跟踪练习
上
外
内
弧 圆上任意两点间的部分叫做弧;圆上任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
小于半圆的弧叫做 ,大于半圆的弧叫做 .
弦 连接圆上任意两点间的线段叫做弦;
过圆心的弦叫做 .
扇形 一条弧和经过这条弧的端点的两条半径所组成的图形
等圆 能够 的圆叫等圆
同心圆 圆心 ,半径 的圆叫做同心圆
劣弧
优弧
直径
相同
不同
重合
直径是圆中最长的弦.
表示优弧时,为了区别于劣弧,要用三个大写字母表示.
圆
12、如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC,若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )A.35°
B.40°
C.60°
D.70°
B
跟踪练习
13、下列说法中正确的个数为 ( )
①同圆中,直径的长等于半径长的2倍;
②过圆心的弦是直径;
③优弧大于劣弧.
A.0 B.1
C.2 D.3
C
当堂检测
第4章
2、已知一个正多边形的每个外角等于60°,则这个正多边形是 ( )
A.正五边形
B.正六边形
C.正七边形
D.正八边形
1、将一个n边形变成n+1边形,内角和将 ( )
A.减少180°
B.增加90°
C.增加180°
D.增加360°
C
C
当堂检测
4、如果把一个多边形的边数增加1倍,它的内角和是2160°,那么原来多边形的边数是 ( )
A.5
B.6
C.7
D.8
3、有两个正多边形,这两个正多边形的边数之比为1∶2,内角和之比为3∶8,则这两个多边形的边数各是 ( )
A.4,8
B.5,10
C.6,12
D.7,14
A
C
当堂检测
5、下列说法错误的是( )
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.能完全重合的两条弧是等弧
B
6、在一个三角形中,已知AB=AC=6cm,BC=8cm,D是BC的中点,以D为圆心作一个半径为5cm的圆,则下列说法正确的是 ( )
A.点A在☉D外
B.点B在☉D上
C.点C在☉D内
D.无法确定
C
当堂检测
7、如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. -180°
B.180°-
C.
D.360°-
A
8、如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是( )
A.5
B.6
C.7
D.8
D
当堂检测
9、如图,∠1、∠2、∠3、∠4是五边形ABCDE的四个外角, 若∠A=120°,则∠1+∠2+∠3+∠4的度数为 .
300°
10、如图,正方形的边长为4,则图中阴影部分的面积为 . .
16-4π
当堂检测
当堂检测
11、如图,CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=120°,∠E=80°,试求∠F的度数.
当堂检测
解:连接AD,在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.
∵AB⊥BC,所以∠B=90°.
又∵∠C=120°,
∴∠BAD+∠ADC=150°.
∵CD∥AF,
∴∠CDA=∠DAF.
∴∠BAF=150°,∠CDE=∠BAF=150°.
又∵六边形ABCDEF的内角和为(6-2)×180°=720°,
∴∠F=720°-∠B-∠C-∠CDE-∠E-∠BAF=130°
当堂检测
12、求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
当堂检测
解:在四边形MCDH中, ∠1+∠C+∠D+∠DHM=360°,
∵∠1=∠A+∠B,
∴∠A+∠B+∠C+∠D=360°-∠DHM,
在四边形EFGH中,∠E+∠F+∠G=360°-∠GHE,
∴∠A+∠B+∠C+∠D+∠E+
∠F+∠G=360°-∠DHM+360°-∠GHE
=360°×2-(∠DHM+∠GHE)
=360°×2-180°=540°
课堂总结
第5章
多边形、正多边形的有关概念及表示
多边形的内、外角和、角平分线计算公式
多边形的密铺
圆的概念、周长面积公式、点与圆的位置关系
弧、等、等圆、同心圆的概念
多边形
圆
多边形与圆
课堂总结
THANK YOU!
2023
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
